Usaco2007 Nov 【Milking Time 】挤奶时间
Usaco2007 Nov 【Milking Time 】挤奶时间
Description
贝茜是一只非常努力工作的奶牛,她总是专注于提高自己的产量。为了产更多的奶,她预计好了接下来的N (1 ≤ N ≤ 1,000,000)个小时,标记为0..N-1。 Farmer John 计划好了 M (1 ≤ M ≤ 1,000) 个可以挤奶的时间段。每个时间段有一个开始时间(0 ≤ 开始时间 ≤ N), 和一个结束时间 (开始时间 < 结束时间 ≤ N), 和一个产量 (1 ≤ 产量 ≤ 1,000,000) 表示可以从贝茜挤奶的数量。Farmer John 从分别从开始时间挤奶,到结束时间为止。每次挤奶必须使用整个时间段。 但即使是贝茜也有她的产量限制。每次挤奶以后,她必须休息 R (1 ≤ R ≤ N) 个小时才能下次挤奶。给定Farmer John 计划的时间段,请你算出在 N 个小时内,最大的挤奶的量。
Input
第1行三个整数N,M,R.接下来M行,每行三个整数Si,Ei,Pi.
Output
最大产奶量.
Sample Input
12 4 2
1 2 8
10 12 19
3 6 24
7 10 31
Sample Output
43
HINT
注意:结束时间不挤奶
正解: DP
很简单的DP
f[i]表示前i时刻能得到的最大产奶量。
然后显然得按时间拍个序,然后就显然了。
Code:
#include int main()
{
// freopen("milkprod.in","r",stdin);
// freopen("milkprod.out","w",stdout);
scanf("%d%d%d",&n,&m,&r);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a[i].st,&a[i].ed,&a[i].p);
}
sort(a+1,a+1+m,cmp);
for(int i=1;i<=m;i++)
{
f[i]=a[i].p;
for(int j=1;jif(a[i].st>=(a[j].ed+r)&&a[i].ed<=n)
f[i]=max(f[i],f[j]+a[i].p);
}
ans=max(ans,f[i]);
}
printf("%d\n",ans);
return 0;
} But!!
☆☆☆重点在这里 ☆☆☆
时间的范围 不大, 1000 左右。那么我们是否可以建一张时间图?
当然我们把休息的Ri算在一项任务中
This‘
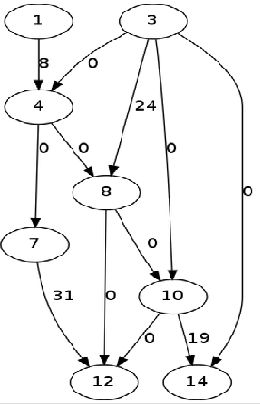
但是上图中我并没有把所有的边连起来,因为大约要有N^2条边,太稠密了。
所以我们可以想办法优化一下。
How?
可以用高等物理中的时间抽象化的思想。把时间看成一条有向坐标轴。从现在指向未来。0->M
而任意两点都用边权为0的有向边相连,每个任务的S,E连边权为VAL_的有向边。像这样:

可以把红线的部分压扁,剩余的有权边想象成弧形,这样就优美多了~
然后跑最长路即可!
最长路怎么搞?
Topsort~
Code:
#include void Topsort()
{
while(!Q.empty())
{
ll u=Q.front();
Q.pop();
for(ll i=head[u];i!=-1;i=edge[i].next)
{
ll v=edge[i].to;
in[v]--;
dis[v]=max(dis[v],dis[u]+edge[i].val);
if(in[v]==0)
{
Q.push(v);
}
}
}
}
int main()
{
//freopen("milkprod.in","r",stdin);
//freopen("milkprod.out","w",stdout);
init();
scanf("%d%d%d",&n,&m,&r);
n+=r;
for(ll i=1;i<=m;i++)
{
scanf("%d%d%d",&a[i].st,&a[i].ed,&a[i].p);
a[i].ed+=r;
if(hash[a[i].st]==0)line[++k]=a[i].st,hash[a[i].st]++;
if(hash[a[i].ed]==0)line[++k]=a[i].ed,hash[a[i].ed]++;
addedge(a[i].st,a[i].ed,a[i].p);
}
if(hash[n]==0)line[++k]=n;
sort(line+1,line+1+k);
for(int i=1;i<=k-1;i++)
{
addedge(line[i],line[i+1],0);
}
Q.push(line[1]);
Topsort();
printf("%d\n",dis[n]);
//fclose(stdin);
//fclose(stdout);
return 0;
}