Problem E. Matrix from Arrays HDU - 6336（容斥+二维前缀和）

Problem E. Matrix from Arrays HDU - 6336

Kazari has an array A length of L, she plans to generate an infinite matrix M using A.
The procedure is given below in C/C++:

int cursor = 0;

for (int i = 0; ; ++i) {
for (int j = 0; j <= i; ++j) {
M[j][i - j] = A[cursor];
cursor = (cursor + 1) % L;
}
}

Her friends don’t believe that she has the ability to generate such a huge matrix, so they come up with a lot of queries about M
, each of which focus the sum over some sub matrix. Kazari hates to spend time on these boring queries. She asks you, an excellent coder, to help her solve these queries.
Input
The first line of the input contains an integer T (1≤T≤100) denoting the number of test cases.
Each test case starts with an integer L (1≤L≤10) denoting the length of A.
The second line contains L integers A0,A1,…,AL−1 (1≤Ai≤100).
The third line contains an integer Q (1≤Q≤100) denoting the number of queries.
Each of next Q lines consists of four integers x0,y0,x1,y1 (0≤x0≤x1≤108,0≤y0≤y1≤108) querying the sum over the sub matrix whose upper-leftmost cell is (x0,y0) and lower-rightest cell is (x1,y1)
.
Output
For each test case, print an integer representing the sum over the specific sub matrix for each query.
Sample Input

1       
3       
1 10 100
5       
3 3 3 3
2 3 3 3
2 3 5 8
5 1 10 10
9 99 999 1000

Sample Output

1
101
1068
2238
33076541

分析：

通过打表可以找到规律，是循环矩阵，奇数是Len，偶数是2*Len,我们都按照2*Len来做就好了，预处理出来前缀和然后容斥的处理询问。

具体如下：

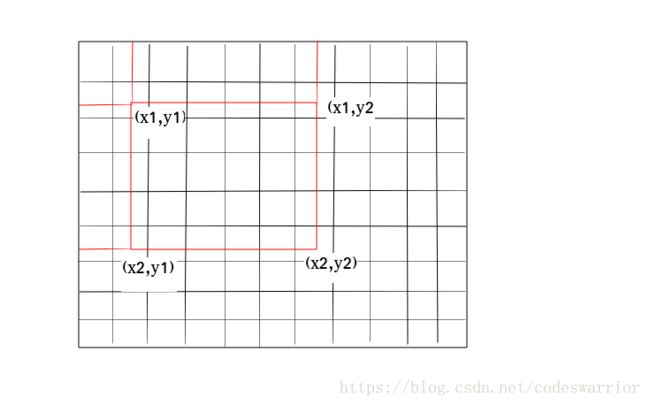
如图我们需要求 （x1,y1）到（x2，y2） （ x 1 , y 1 ） 到 （ x 2 ， y 2 ） 之间的矩形面积

可以根据前缀和思想

最左上角代表(0,0)处

所以我们求出从（0,0）开始的前缀和

getsum[x2][y2],getsum[x2][y1−1],getsum[x1−1][y2],getsum[x1−1][y1−1] g e t s u m [ x 2 ] [ y 2 ] , g e t s u m [ x 2 ] [ y 1 − 1 ] , g e t s u m [ x 1 − 1 ] [ y 2 ] , g e t s u m [ x 1 − 1 ] [ y 1 − 1 ]

这样我们的答案

ans=getsum[x2][y2]−getsum[x2][y1−1]−getsum[x1−1][y2]+getsum[x1−1][y1−1] a n s = g e t s u m [ x 2 ] [ y 2 ] − g e t s u m [ x 2 ] [ y 1 − 1 ] − g e t s u m [ x 1 − 1 ] [ y 2 ] + g e t s u m [ x 1 − 1 ] [ y 1 − 1 ]

但是我们只记录下了每个单位循环矩阵的前缀和 sum[x][y] s u m [ x ] [ y ] ，因此对于每个getsum值我们需要一一求出

---

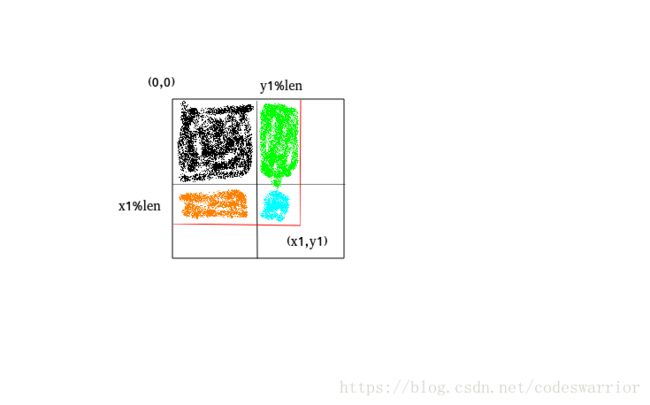
我们以求左上角的小部分为例，即 getsum[x1−1][y1−1] g e t s u m [ x 1 − 1 ] [ y 1 − 1 ] 的求法：

如图

我们可以求出各个边长
并且可以分成四部分来算：完整循环矩阵和+下面长条+右边长条+右下角小块

1）这样我们先算出整个的循环矩阵有多少个应该是

x1len×y1len x 1 l e n × y 1 l e n

因为是完整的矩阵所以这部分的和应该是

x1len×y1len×sum[len][len] x 1 l e n × y 1 l e n × s u m [ l e n ] [ l e n ]

2）下面长条应该是

sum[x1%len][len]×y1len s u m [ x 1 % l e n ] [ l e n ] × y 1 l e n

3) 右边长条应该是

sum[len][y1%len]×x1len s u m [ l e n ] [ y 1 % l e n ] × x 1 l e n

4) 右下角小块应该是

sum[x1%len][y1%len] s u m [ x 1 % l e n ] [ y 1 % l e n ]

然后四部分加起来即可

这样我们可以写个函数，每次直接调用即可

---

code:

#include 
using namespace std;
typedef long long ll;
ll M[110][110];
ll A[15],len,L;
ll sum[25][25];
ll getsum(int x,int y){
    ll ans = (x / len) * (y / len) * sum[len][len];
    ans += sum[x%len][len] * (y / len);
    ans += sum[len][y%len] * (x / len);
    ans += sum[x%len][y%len];
    return ans;
}
int main(){
    int t,q;
    int x1,x2,y1,y2;
    scanf("%d",&t);
    while(t--){
        scanf("%lld",&L);
        len = L * 2;
        memset(sum,0,sizeof(sum));
        for(int i = 0; i < L; i++) scanf("%lld",&A[i]);
        ll cursor = 0;
        for(int i = 0; i <= 100; i++){
            for(int j = 0; j <= i; j++){
                M[j+1][i-j+1] = A[cursor];
                cursor = (cursor + 1) % L;
            }
        }
        for(int i = 1; i <= len; i++){
            for(int j = 1; j <= len; j++){
                sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + M[i][j];
            }
        }
        scanf("%d",&q);
        while(q--){
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            x1++,y1++,x2++,y2++;
            ll ans = getsum(x2,y2) - getsum(x2,y1-1) - getsum(x1-1,y2) + getsum(x1-1,y1-1);
            printf("%lld\n",ans);
        }
    }
    return 0;
}