Inorder Successor in Binary Search Tree BST中找中序遍历的后继节点
BST中找中序遍历的后继节点
两点注意:
1. 这个BST是否有parent指针:如果有,则直接用父指针往上找。如果没有,则从root开始往下找。
2. 要查找的点是否有右孩子:如果有,简单,直接找右子树的最小节点。如果没有,则找到比该节点大且相差最小的父节点
时间复杂度都是O(h), h是树高
In Binary Tree, Inorder successor of a node is the next node in Inorder traversal of the Binary Tree. Inorder Successor is NULL for the last node in Inoorder traversal.
In Binary Search Tree, Inorder Successor ofan input node can also be defined as the node with the smallest key greater than the key of input node. So, it is sometimes important to find next node in sorted order.
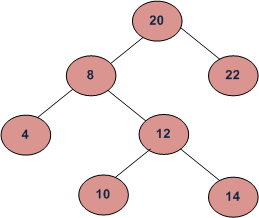
In the above diagram, inorder successor of8is10, inorder successor of10is12and inorder successor of14is20.
Method 1 (Uses Parent Pointer)
In this method, we assume that every node has parent pointer.
The Algorithm is divided into two cases on the basis of right subtree of the input node being empty or not.
Input:node, root//nodeis the node whose Inorder successor is needed.
output:succ//succis Inorder successor ofnode.
1)If right subtree ofnodeis notNULL, thensucclies in right subtree. Do following.
Go to right subtree and return the node with minimum key value in right subtree.
2)If right sbtree ofnodeis NULL, thensuccis one of the ancestors. Do following.
Travel up using the parent pointer until you see a node which is left child of it’s parent. The parent of such a node is thesucc.
Method 2 (Search from root)
Parent pointer is NOT needed in this algorithm. The Algorithm is divided into two cases on the basis of right subtree of the input node being empty or not.
Input:node, root//nodeis the node whose Inorder successor is needed.
output:succ//succis Inorder successor ofnode.
1)If right subtree ofnodeis notNULL, thensucclies in right subtree. Do following.
Go to right subtree and return the node with minimum key value in right subtree.
2)If right sbtree ofnodeis NULL, then start from root and us search like technique. Do following.
Travel down the tree, if a node’s data is greater than root’s data then go right side, otherwise go to left side.
package BinaryTreeSummary;
public class BSTInorderSuccessor {
public static void main(String[] args) {
Node root = null;
root = insert(root, 20);
root = insert(root, 8);
root = insert(root, 22);
root = insert(root, 4);
root = insert(root, 12);
root = insert(root, 10);
root = insert(root, 14);
Node temp = root.left.right.right;
Node succ = inorderSuccessor(root, temp);
succ = inorderSuccessor2(root, temp);
if (succ != null) {
System.out.println(temp.data + "'s successor is " + succ.data);
} else {
System.out.println("error");
}
}
// 1)需要parent指针的做法
// 找inorder successor 分右孩子是否存在的两种情况考虑
// O(h) h: height of tree
public static Node inorderSuccessor(Node root, Node node) {
if (node.right != null) { // 有右孩子,直接找右子树的最小节点
return minValue(node.right);
}
// 否则利用父指针不断向上找,直到父节点的值大于当前节点的值
// 或者该节点成为父节点的右孩子
Node parent = node.parent;
// while (parent != null && node == parent.right) {
while (parent != null && node.data > parent.data) {
node = parent;
parent = parent.parent;
}
return parent;
}
// 2)不需要parent指针的做法
// 过程其实就是个从root查找node节点的过程,同时保存旧的比node大的root节点,作为succ
// O(h)
public static Node inorderSuccessor2(Node root, Node node) {
if (node.right != null) { // 有右孩子,直接找右子树的最小节点
return minValue(node.right);
}
Node succ = null;
while(root != null) {
if(root.data > node.data) { // 继续找更小的
succ = root; // 后继节点必然比node要大,所以只能在这里保存
root = root.left;
}
else if(root.data < node.data){ // 继续找更大的
root = root.right;
}
else{ // root节点和node节点重复,停止
break;
}
}
return succ;
}
/*
* Given a non-empty binary search tree, return the minimum data value found
* in that tree. Note that the entire tree does not need to be searched.
*/
public static Node minValue(Node node) {
Node cur = node;
// 最小节点必定在最左下角
while (cur.left != null) {
cur = cur.left;
}
return cur;
}
/*
* Give a binary search tree and a number, inserts a new node with the given
* number in the correct place in the tree. Returns the new root pointer
* which the caller should then use (the standard trick to avoid using
* reference parameters).
*
* 返回插入后节点的引用
*/
public static Node insert(Node node, int data) {
if (node == null) {
return new Node(data);
} else { // node 存在
Node temp;
if (data <= node.data) {
temp = insert(node.left, data);
node.left = temp;
temp.parent = node;
} else {
temp = insert(node.right, data);
node.right = temp;
temp.parent = node;
}
return node;
}
}
static class Node {
int data;
Node left;
Node right;
Node parent;
public Node(int data) {
this.data = data;
}
}
}
http://www.geeksforgeeks.org/inorder-successor-in-binary-search-tree/