多重共线性的诊断(R语言)
多重共线性的诊断
1.方差扩大因子法
经验表明, V I F j ≥ 10 VIF_{j}\geq10 VIFj≥10时,就说明自变量 x j x_{j} xj与其余变量之间有严重的多重共线性,且这种多重共线性可能会过度地影响最小二乘估计值。
代码实现如下:
data3.3<-read.csv("C:/Users/Administrator/Desktop/data3.3.csv",head=TRUE)
lm3.3<-lm(y~x1+x2+x3+x4+x5,data3.3)
library(car)
vif(lm3.3)
输出结果为:
![]()
从输出结果看到, x 1 , x 2 x1,x2 x1,x2的方差扩大因子很大,远远超过10 ,说明这四个变量之间存在严重的多重共线性。
一般情况下,当一个回归方程存在严重的多重共线性时,有若干个自变量所对应的方差扩大因子大于10,这个回归方程多重共线性的存在就是由方差扩大因子超过10 的这几个变量引起的,说明这几个自变量之间有一定的多重共线性的关系存在。知道了这一点,对于我们消除回归方程的多重共线性非常有用。
2.特征根判定法
通常认为条件数 k < 100 k<100 k<100时,设计矩阵 X X X多重共线性的程度很小; 100 ≤ k ≤ 1000 100\leq k\leq 1000 100≤k≤1000时,设计矩阵 X X X存在较强的多重共线性; k > 1000 k>1000 k>1000时,存在严重的多重共线性。
代码实现如下:
data3.3<-read.csv("C:/Users/Administrator/Desktop/data3.3.csv",head=TRUE)
XX<-cor(data3.3[,2:6])
kappa(XX,exact=TRUE)
输出结果为:
![]()
根据条件数大于1000,说明自变量之间存在严重的多重共线性。为找出哪些变量是多重共线性的,需要计算矩阵的特征值和相应的特征向量,在R命令窗口下面代码:
eigen(XX)
输出结果为:
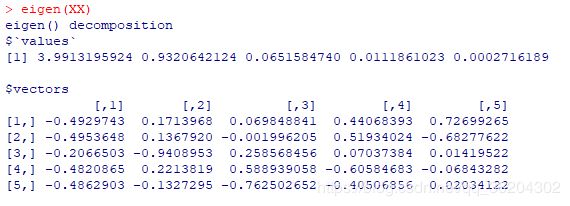
有结果知道相应的特征向量为
φ = ( 3.99 , 0.93 , 0.07 , 0.01 , 0 ) T \varphi=(3.99,0.93,0.07,0.01,0)^{T} φ=(3.99,0.93,0.07,0.01,0)T
即 3.99 X 1 ∗ + 0.93 X 2 ∗ + 0.07 X 3 ∗ + 0.01 X 4 ∗ ≈ 0 3.99X_{1}^{*}+0.93X_{2}^{*}+0.07X_{3}^{*}+0.01X_{4}^{*}\approx0 3.99X1∗+0.93X2∗+0.07X3∗+0.01X4∗≈0。由于 X 3 ∗ , X 4 ∗ , X 5 ∗ X_{3}^{*},X_{4}^{*},X_{5}^{*} X3∗,X4∗,X5∗的系数几近于0,故 X 1 ∗ X_{1}^{*} X1∗和 X 2 ∗ X_{2}^{*} X2∗之间存在着多种共线性。