Dijkstra算法及其优化——最短路算法
Dijkstra算法(一下简称Dij),是目前主流的求最短路的方法,自从CCF出题人公开表明SPFA它死了,并且在2018年卡了一次毒瘤数据SPFA,SPAF便退下主流最短路之位。
Dij实在每次进行扩展时,都去找相邻且离起点最近的点,这样就能达到最短路当前最优,但是并不代表未来最优,但是我们现在不考虑,那是Astar的事。
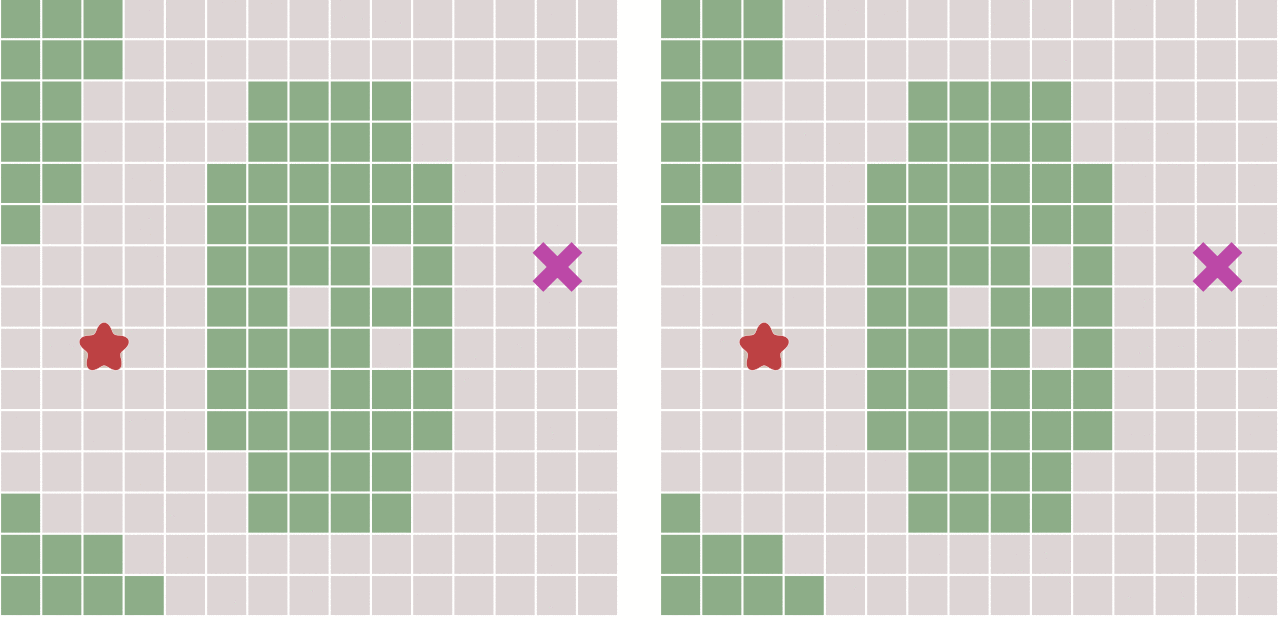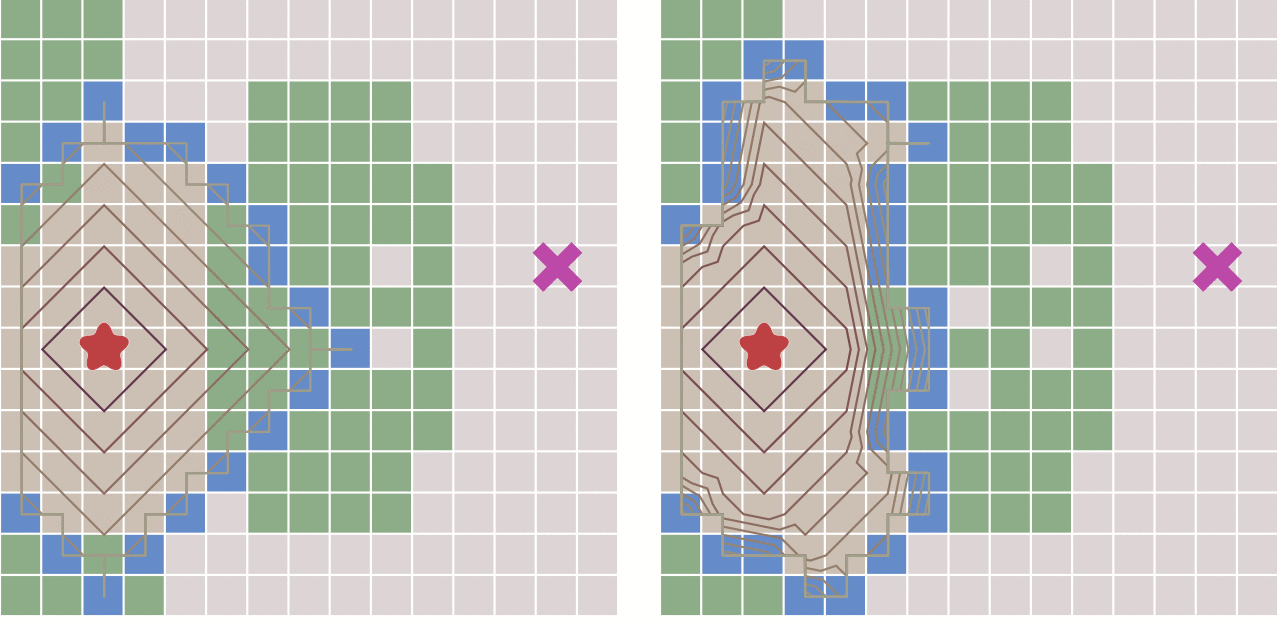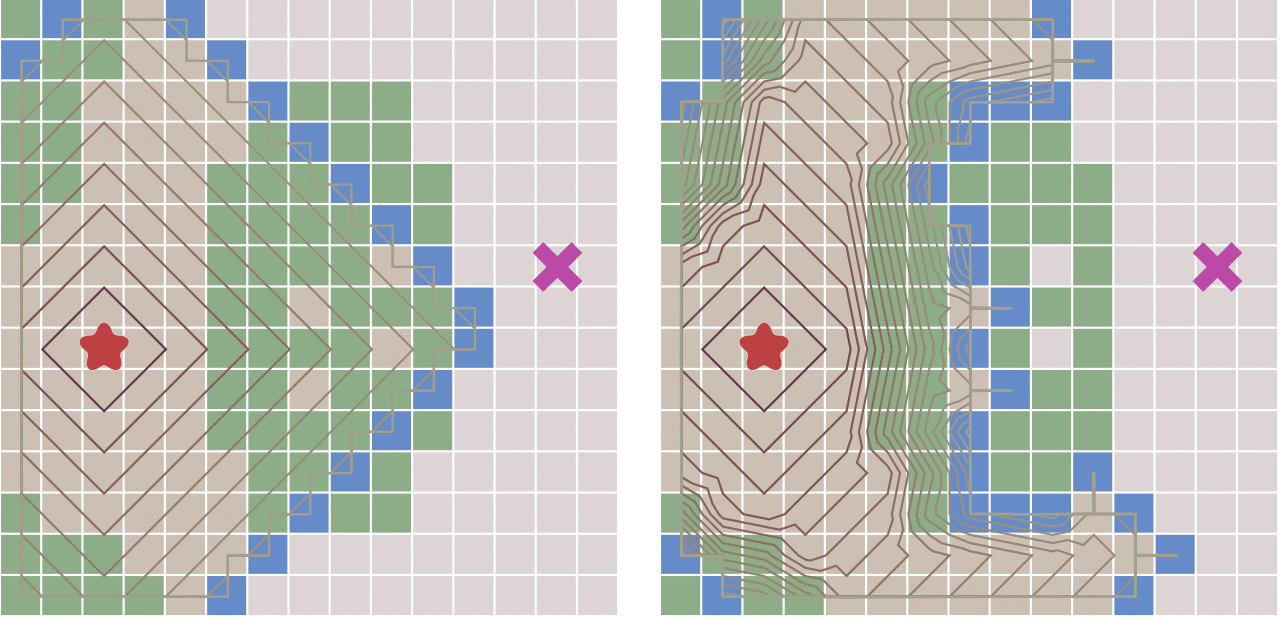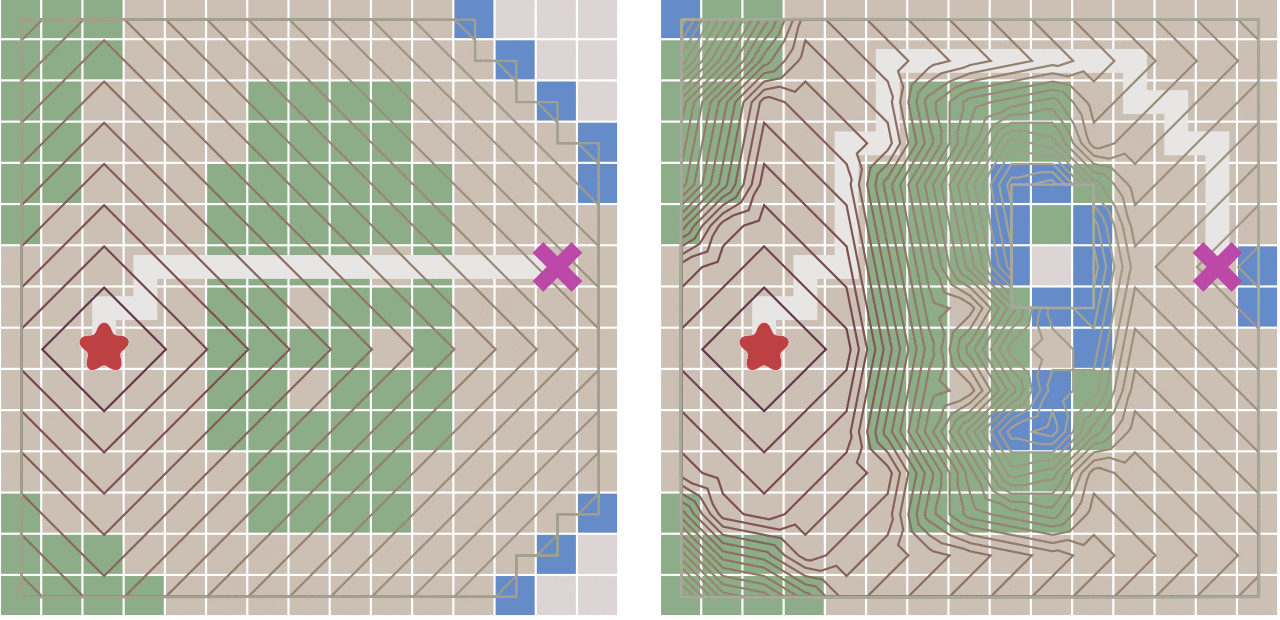
Dij算法如上右图,BFS如左图,可见,BFS不能处理带权的最短路,只是暴力的扩展,而Dij可以。
下面我们通过一道例题来理解Dij的代码实现。
热浪
输入
第1行:4个由空格隔开的整数T,C,Ts,Te.
第2到第C+1行:第i+l行描述第i条道路.有3个由空格隔开的整数Rs,Re,Ci.
输出
一个单独的整数表示Ts到Te的最小费用.数据保证至少存在一条道路.
样例
输入
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
输出
7
这道题就是最短路的板子题,SPFA可以过,好像Floyd和Bellman也可以过,但我们今天讲Dij。
思路:
Dij是从起点开始,每次找一遍相邻的所有点,找出离起点最短距离最小的点(Dij的核心思路),再在这个点上扩展, d i s t [ v ] = m i n ( d i s t [ v ] , d i s t [ u ] + e d g e [ i ] ) dist[v]=min(dist[v],dist[u]+edge[i]) dist[v]=min(dist[v],dist[u]+edge[i])其中 d i s t [ v ] dist[v] dist[v]表示当前找到的最短路距离, d i s t [ u ] dist[u] dist[u]表示开始的点的最短路距离, e d g e [ i ] edge[i] edge[i]表示边权。当然实际不能这么写,还需要判断是否被访问过,用堆优化还要将这个点放进队列
所以就来看看Dij的代码吧。
#include 所以不难看出,Dij的时间复杂度是 O n 2 On^2 On2,在某些毒瘤数据下,还是会超时,主要的时间浪费由找离出发点距离最小的点,有没有什么办法可以优化这一过程呢?这是我们就看向了 S T L STL STL,然后找到了一个奇怪逆天的东西——优先队列也就是大根堆—— p r i o r i t y _ q u e u e priority\_queue priority_queue,这种数据结构的特点是会将最大的元素放到堆顶,使用它就可以避免去慢慢地遍历1-n来寻找最小的距离了,但是由于它的堆顶是取的当然堆里的最大值,为了让堆顶变成我们想要的最小值,我们只需要在放元素进去时将其转换成负数,这样绝对值最小的就在堆顶上面,在取出来时在变回来就可以找到我们想要的最小值了。
那我们先来看一看怎样操作这种数据结构。
priority_queue<int >q;//定义
q.push(1);//放入元素
int a=q.top();//取堆顶
q.pop();//弹出堆顶
但是还要注意一个地方,如过我们只将 d i s t dist dist的值放进去后,虽然我们知道了最小值是什么,但是我们根本不能从茫茫数据中找出它是那个点的最短路,所以我们用结构体来存储编号和最短路,这样做就必须还要重载 < < <运算符,来让堆明白它是应该给结构体里的最短路排序。并且在这里还可以将小于符号就重载成小于符号感觉怪怪的,从而直接使堆变为小根堆,从而避免变负号的麻烦操作。
bool operator < (node a,node b){
return a.dis>b.dis;//大根堆
}
代码如下:
#include
dis[v]=dis[u]+edge[i];
q.push(node(v,dis[v]));
}
}
}
}
int main() {
cin>>n>>m>>s>>t;
for(int i=1; i<=m; i++) {
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dij(s);
cout<<dis[t];
return 0;
}