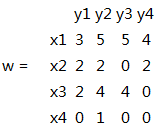初涉二分图的最大权匹配 KM算法
对于一个赋权的二分图可以用KM算法求解最大权匹配的前提是该二分图存在完美匹配。
若此二分图不存在完美匹配,则有两种方法。一是转化成网络流问题求解。二是添加一些点和权为0的边使其变为赋权完全二分图。
显然对于任何二分图通过第二种方法均能转化为存在完美匹配的二分图,且结果不会改变。故KM算法可以求解所有带权二分图的最大权匹配。
KM算法中用到的几个概念:可行性标号,相等子图,交错树。
用L[ u ] 表示 u 的标号,w[u,v] 表示两点连边的权值。
可行性标号:若对于赋权二分图 G = (X,Y) 有 L[ x ] + L[ y ] >= w[ x, y ] (x ∈ X,y ∈ Y)。则称L[]为可行性标号。
赋权二部图的可行性标号总是存在的。
一种平凡的可行性顶点标号是对于 u ∈(X∪Y),有
若 u ∈X,L[ u ] = max(w[ u , y ])。
若 u∈Y,L[ v ] = 0。
相等子图: 设G是一个赋权二部图,G 以 {edge[x,y] | x ∈ X,y∈Y,L[ x ] + L[ y ] == w[x,y]} 为边集的生成子图成为G的相等子图。
设G的相等子图为G‘,则G’与G的点集相同。
鉴于叙述能力有限,直接上图:
图G各边以邻接矩阵的方式存储。
图G及其平凡标号:
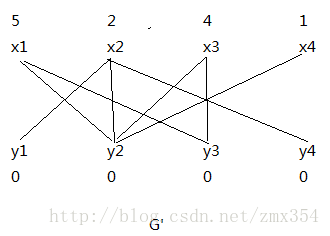
G的相等子图:
学这个算法的时候被这个交错树概念狠狠地绊了一脚。必须好好记一下。
交错路:设 M 为 G的一个匹配,P为G的一条路,E(G) 为图G的边集。如果P中的边在 M 与 E(G) - M 中交替出现,则称P为M-交错路。
交错树:设 M 为 G的一个匹配,u 是 X 的m非饱和点,若存在树H 包含于 G,且满足下面两个条件:
1.u ∈ V(H);
2.对H的每个顶点 v , H中唯一的 u-v 路是一条M-交错路。
则称 H 是一棵以 u 为根的M-交错树。
继续上图:
图G,粗线为G的一个匹配M。
以x1为根的交错树。
KM算法:
设G为赋权二分图,L[ ] 为G的可行性顶标,GL为有L[]确定的G的相等子图。
若G不为完全二部图,则添加一些顶点和权为0的边,L[ ] 初始化为平凡的顶点标号。
1.对于L[],确定G的相等子图GL。
2.利用匈牙利算法对GL求完美匹配M,若存在M,则M即为最大权匹配,算法终止。否则匈牙利算法必终止于一棵交错树 H ,转第三步。
3.计算 α = min{L[x]+L[y]-w[x,y] | x,y∈V(H),x∈X,y∈(Y-Y∩V(H) )}.并按下式更新L[]。
然后转步骤一。
每次更新L[] 有:
1.对于两端点均在交错树上的边,不会影响其属性,即原先存在于相等子图现在仍存在于相等子图。
2.对于两端点均不在交错树上的边,2不会影响其属性,即原先存在于相等子图现在仍存在于相等子图,反之亦然。
3.对于有且仅有一个端点在交错树上的边,有可能会改变其属性,即被移出或移入相等子图。
1.当X端点在交错树上时,L[x] + L[y] 减小,故有可能进入。
2.当Y端点在交错树上时,L[x] + L[y] 增加,故有可能删除。
*本文只记算法的操作流程,证明详见《图论及其算法》,《图论与网络流理论》等相关书籍。如有错误,敬请指出。