2015NOIP普级组第三题--求和(参考洛谷题解)
一、题目描述
一条狭长的纸带被均匀划分出了n个格子,格子编号从1到n。每个格子上都染了一种颜色color_i用[1,m]当中的一个整数表示),并且写了一个数字number_i。
定义一种特殊的三元组:(x,y,z),其中x,y,z都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
-
xyz是整数,x
- colorx=colorz
满足上述条件的三元组的分数规定为(x+z)*(number_x+number_z)。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以10,007所得的余数即可。
输入输出格式
输入格式:
第一行是用一个空格隔开的两个正整数n和m,n表纸带上格子的个数,m表纸带上颜色的种类数。
第二行有n用空格隔开的正整数,第i数字number表纸带上编号为i格子上面写的数字。
第三行有n用空格隔开的正整数,第i数字color表纸带上编号为i格子染的颜色。
输出格式:
共一行,一个整数,表示所求的纸带分数除以10,007所得的余数。
输入输出样例
6 2 5 5 3 2 2 2 2 2 1 1 2 1
82
15 4 5 10 8 2 2 2 9 9 7 7 5 6 4 2 4 2 2 3 3 4 3 3 2 4 4 4 4 1 1 1
1388
说明
【输入输出样例 1 说明】
纸带如题目描述中的图所示。
所有满足条件的三元组为: (1, 3, 5), (4, 5, 6)。
所以纸带的分数为(1 + 5)*(5 + 2) + (4 + 6)*(2 + 2) = 42 + 40 = 82。
对于第 1 组至第 2 组数据, 1 ≤ n ≤ 100, 1 ≤ m ≤ 5;
对于第 3 组至第 4 组数据, 1 ≤ n ≤ 3000, 1 ≤ m ≤ 100;
对于第 5 组至第 6 组数据, 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000,且不存在出现次数
超过 20 的颜色;
对 于 全 部 10 组 数 据 , 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000, 1 ≤ color_i ≤ m,1≤number_i≤100000
二、解题思路
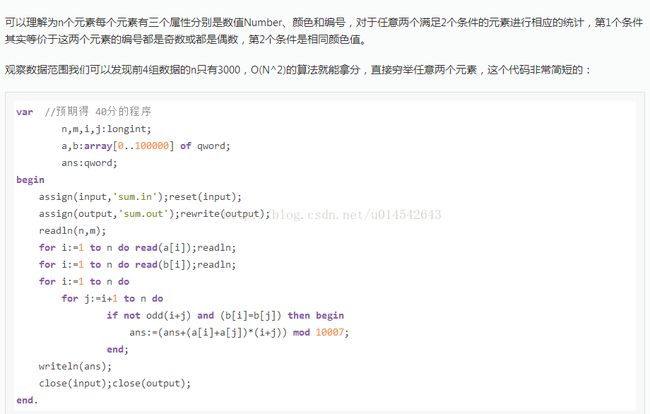
可以理解为 n 个元素每个元素有三个属性分别是数值 Number、颜色和编号,对于任意 两个满足 2 个条件的元素进
行相应的统计,第 1 个条件其实等价于这两个元素的编号都是奇 数或都是偶数,第 2 个条件是相同颜色值。
根据题目,我们可以设有三个下标,他们分别是x,y,z,要满足x 所以我们可以模拟x,y,z,其时间复杂度为O(n^3),由于n<=100000所以一定会超时 但这个方法是可以优化的 由此我们可以得到2y=z+x 由此可知z+x必须是一个偶数即z,x同为奇数或同为偶数 所以我们其实只要穷举x和z就行了,但这个方法的时间复杂度为O(n^2)所以还是会超时 我们可以用一下分组思想,把每个颜色分为一组,再在每个颜色中按奇偶分组,所以一共有2m组 设一个分组里有k个数,这个分组中的数分别是x[1],x[2]……x[k],下标分别是y[1],y[2]……y[k] 可以使用排序,将颜色、奇偶性相同的放在一起求和,再将每个分类的和相加。 这种做法即使使用 QS 或 HS ,时间复杂度也在 O(log2(n))。 可以定义三个数组,存储每个分类的编号和、数字和,最后再进行求和。 此时只需将数组每个元素调用一次即可得到答案,时间复杂度为 O(n)。 分析一下,我们的任务是什么。题目的要求是求分数和,我们就得把所有符合条件的三元组“找”出来。 至少需要枚举三元组(x,y,z)中的一个元素,这里枚举的是z(当然x也可以,不过不要选y,因为y对分数没什么用)。 1、因为x 2、因为y-x=z-y,所以x+z=2y,x、z同奇偶,且分数与y物管,只需枚举z和x。 3、因为colourx=colourz,所以只需枚举z之前同奇偶且同色的x。 这样的话时间复杂度是O(n2),能得40分。如何快速枚举x呢? 其实不是快速枚举x,是快速枚举分数和。 观察三元组分数: (x+z)·(numberx+numberz) 显然我们不方便处理多项式乘法,那就把它拆开 (事实上很多人到这步都放弃了,其实试一试立刻就明白了) =x·numberx+x·numberz+z·numberx+z·numberz 那么对于z的所有合法决策x1,x2,……,xk 根据乘法分配率,分数=Σ(xi*numberxi)+Σ(xi)*numberz +Σ(numberxi) *z+Σ(z*numberz) (1<=i<=k) 由于z是枚举的,所以只需快速得到Σ(x·numberx),Σx,Σnumberx和k(注意最后一项被算了k次,要乘k) 这样我们就可以开4个累加器,分别记录这四个量。而对于不同奇偶性、不同颜色的z有不同的决策x,所以要开一个s[2][m][4]的累加器。 【时空复杂度】 O(n),O(n+m) 【注意】题目数据较大,每次计算一定要模10007,否则很容易出错。 三、实现代码 #include #include struct cell { int clr;//编号 long long num;//数字 long long cod;//分类 }c[100001]; int main() { int i,n,m,clrmx=0; long long t=0,t1[200002],t2[200002],t3[200002],k[200002]; memset(t1,0,sizeof(t1)); memset(t2,0,sizeof(t2)); memset(t3,0,sizeof(t3)); memset(k,0,sizeof(k)); scanf("%d%d",&n,&m); for(i=1;i<=n;i++) { c[i].cod=i; scanf("%lld",&c[i].num); } for(i=1;i<=n;i++) { scanf("%d",&c[i].clr); c[i].clr*=2; c[i].clr+=c[i].cod%2; }//输入 for(i=1;i<=n;i++) { int f=c[i].clr;//当前纸带的分类 if(f>clrmx)clrmx=f; t1[f]+=c[i].cod*c[i].num; t1[f]%=10007; t2[f]+=c[i].cod; t3[f]+=c[i].num; k[f]++; }//遍历 for(i=1;i<=clrmx;i++) { t2[i]%=10007; t3[i]%=10007; k[i]%=10007; t+=(k[i]-2)*t1[i]+t2[i]*t3[i]; t%=10007; }//求和 printf("%lld",t); }