今年难度大了很多,也有很多毒瘤题..
这篇博客尝试详尽地解析NOIP2018普及初赛.
题目
答案
先附上答案
单项选择题
1.C
送分题 其他都是输入设备
2.D
A: $(269)_{16}=617$
B: $617$
C: $(1151)_{8}=617$
D: $(1001101011)_{2}=619$
3.D
常识性知识
$1GB=1024KB=1024*1024B$
4.A
广域网-Wide Area Network-WAN
想Wide就可以了
5.B
CCF赞歌,最近几乎每年都有。
直接拿今年年份减去届数(2018-24=1984)。
6.A
小学奥数。在历年的基础上改了下。每8个字母($ASDFasdf$)一个循环,$81%8=1$,所以为A.
7.A
可以正经推出。但考试的时候如果不知道那可以画几个例子,然后带进去算。算出来A为正确。
注意本题树根深度记做0.
8.A
基数排序就是桶排序,所以不用比较。
没听说过?
B.冒泡和D.插入一定知道吧,都需要对比。C.堆排,堆的数据插入后上浮下沉操作需要比对,所以排除法选A。
9.A
看题目首先排除C和D。
然后时间复杂度一般要考虑最坏所以向上取整(然而我还是错了)。
10.B
送分。
11.C
分类讨论。
如下所示:
12.B
注意空集
13.B
小学奥数,分解质因数$10000=2^4*5^4$,2的倍数有4999个,5的倍数有1999个,除去10(2和5的公倍数)999个,加上10000这一个数,不互质的就是6000个,互质的就是10000-6000=4000个
14.B
状压DP常规操作,实在不行模拟也可。
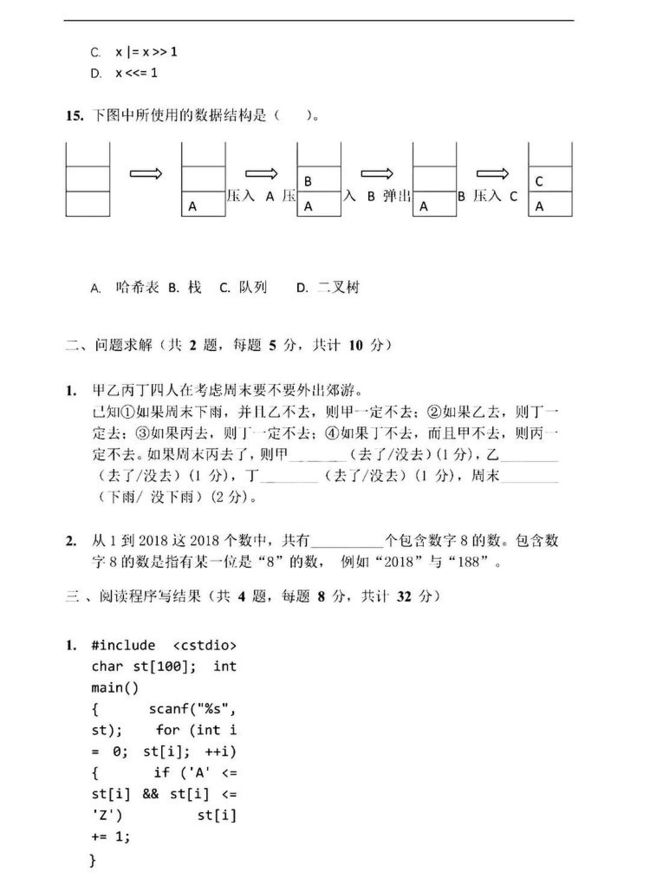
15.B
不用多说,先进先出,栈。
问题求解
1
小学奥数,从③推出丁不去,又从④推出甲去了,然后由①推出没下雨。
2
分类讨论。
1-9中:1个
10-99中:1*8+10=18个
100-999中:(1+18)*8+100=252个
1000-1999中:1+18+252=271个
2000-2018中:2个
总共 1+18+252+271+2=544个
注意最后的2个要加上去,我是不会说我没加的。
阅读程序写结果
1
#include
char st[100];
int main() {
scanf("%s", st);
for (int i = 0; st[i]; ++i) {
if ('A' <= st[i] && st[i]<= 'Z')
st[i] += 1;
}
printf("%s\n", st);
return 0;
}
读题意就是将所有大写字母变成字母后一位,如'A'变成'B','E'变成'F'.
输出:RuanHuoMianTai
2
#include
int main()
int x;
scanf("%d",&x);
int res = 0;
for (int i=0;i 读题意得 0-15 每一个数的平方模15 是不是等于1
枚举和模的时候要细心
输出:4
3
#include
using namespace std;
int n,m;
int findans(int n,int m){
if (n==0) return m;
if (m==0) return n % 3;
return findans(n-1,m)-findans(n,m-1)+findans(n-1,m-1);
}
int main(){
cin>>n>>m;
cout< 做的时候暴力模拟,后来知道可以用表格。
$f[i][j]=f[i-1][j]-f[i][j-1]+f[i-1][j-1]$
表格长这样
| n/mn/m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | -1 | 4 | 1 | 6 | 3 | 8 |
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 5 | 2 | -1 | 4 | 1 | 6 | 3 | 8 |
输出:8
4
#include
int n,d[100];
bool v[100];
int main(){
scanf("%d",&n);
for (int i=0;i 暴力模拟即可
输出:6
完善程序
1.最大公约数之和
(1)
$i*i$,枚举到$\sqrt{n}$
(2)
$n/i$
(3)
return a
(4)
a%b
(5)
gcd(a[i],a[j])+ans
2.双向链表求排列
(1)
a[x]=i
(2)
i+1
(3)
R[a[i]],对称填
(4)
a[i],刚开始对称填错了,双向链表操作
(5)
R[i]