概念
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。
基本思想
要解决一个给定的问题,我们需要解决其不同部分(即解决子问题),再合并子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图只解决每个子问题一次,从而减少计算量。
一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。
这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
动态规划有三个核心元素:
1.最优子结构
2.边界
3.状态转移方程
我们来看一到题目
题目
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。求出一共有多少种走法。
比如,每次走1级台阶,一共走10步,这是其中一种走法。
再比如,每次走2级台阶,一共走5步,这是另一种走法。
但是这样一个个算太麻烦了,我们可以只去思考最后一步怎么走,如下图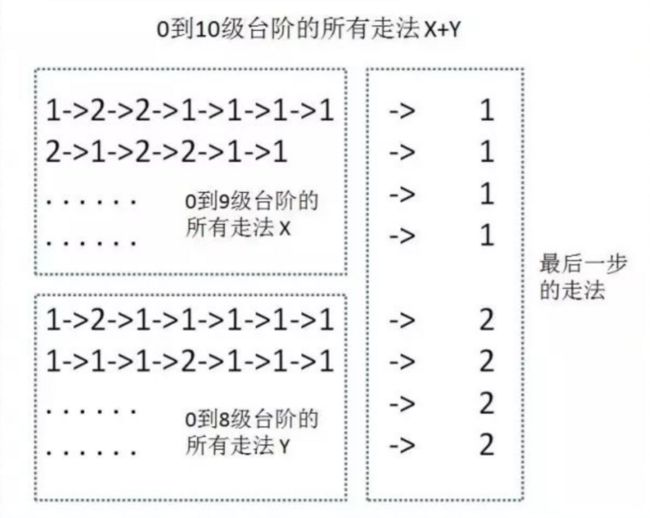
这样走到第十个楼梯的走法 = 走到第八个楼梯 + 走到第九个楼梯
我们用f(n)来表示 走到第n个楼梯的走法,所以就有了f(10) = f(9) + f(8)
然后f(9) = f(8) + f(7), f(8) = f(7) + f(6)......
这样我们就得出来一个递归式:
f(n) = f(n-1) + f(n-2);
还有两个初始状态:
f(1) = 1;
f(2) = 2;
这样就得出了第一种解法
方法一:递归求解
function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; return getWays(n-1) + getWays(n-2); }
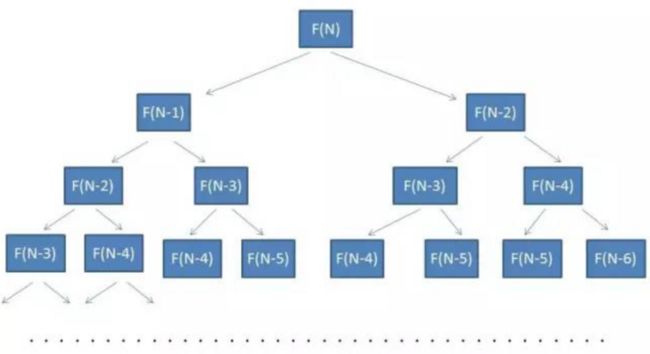
可以看到这是一颗二叉树,数的节点个数就是我们递归方程需要计算的次数,
数的高度为N,节点个数近似于2^n
所以时间复杂度近似于O(2^n)
但是这种方法能不能优化呢?
我们会发现有些值被重复计算,如下图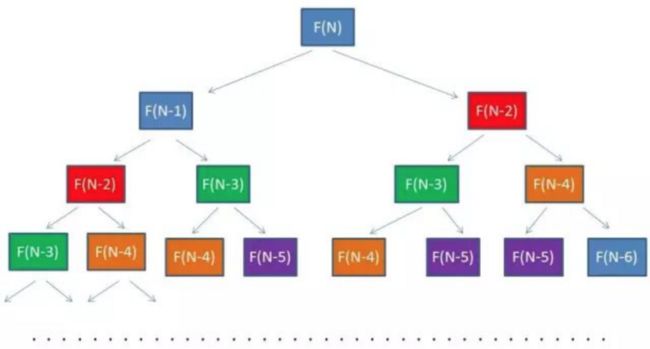
相同颜色代表着重复的部分,那么我们可不可以把这些重复计算的值记录下来呢?
这样的优化就有了第二种方法
方法二:备忘录算法
const map = new Map(); function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; if (map.has(n)) { return map.get(n); } const value = getWays(n-1) + getWays(n-2); map.set(n, value); return value; }
因为map里最终会存放n-2个键值对,所以空间复杂度为O(n),时间复杂度也为O(n)
继续想一想这就是最优的解决方案了吗?
我们回到一开始的思路,我们是假定前面的楼梯已经走完,只考虑最后一步,所以才得出来f(n) = f(n-1) + f(n-2)的递归式,这是一个置顶向下求解的式子
一般来说,按照正常的思路应该是一步一步往上走,应该是自底向上去求解才比较符合正常人的思维,我们来看看行不行的通

这是进行了一次迭代得出了3个楼梯的走法,f(3)只依赖于f(1) 和 f(2)
继续看下一步
这里又进行了一次迭代得出了4个楼梯的走法,f(4)只依赖于f(2) 和 f(3)
我们发现每次迭代只需要前两次迭代的数据,不用像备忘录一样去保存所有子状态的数据
方法三:动态规划求解
function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; // a保存倒数第二个子状态数据,b保存倒数第一个子状态数据, temp 保存当前状态的数据 let a = 1, b = 2; let temp = a + b; for (let i = 3; i <= n; i++) { temp = a + b; a = b; b = temp; } return temp; }
这是我们可以再看看当前的时间复杂度和空间复杂度
当前时间复杂度仍为O(n),但空间复杂度降为O(1)
这就是理想的结果
总结
这只是动态规划里最简单的题目之一,因为它只有一个变化维度
当变化维度变成两个、三个甚至更多时,会更加复杂,背包问题就是比较典型的多维度问题,有兴趣的可以去网上看看《背包九讲》