dijkstra——堆优化
在图的算法中我们有不少优秀的算法,今天来记录一下我最近看dijkstra的收获,有大佬发现不对的地方请指正。
dijkstra
dijkstra是一种求解单源最短路径的算法,值得注意的是,它只能应用于边权非负的情况。
dijkstra算法主要利用松弛操作来获取比当前更优的情况,多次操作后,获得最优解。
松弛操作:
我们定义目标点 S S S到其他点 X X X的最短距离为为 d i s S − X dis_{S-X} disS−X
假如目前已知目标点 S S S到 A A A点的距离为 d i s S − A dis_{S-A} disS−A,如果有另一个点 B B B, d i s S − B dis_{S-B} disS−B, d i s S − A > d i s S − B + d i s B − A dis_{S-A}>dis_{S-B}+dis_{B-A} disS−A>disS−B+disB−A,那么 d i s S − A dis_{S-A} disS−A的值不是最小的,那么肯定要更新为 d i s S − B + d i s B − A dis_{S-B}+dis_{B-A} disS−B+disB−A,这个过程就叫松弛。
最朴素的dijkstra:
把已经找到最小距离的点分为一组A,剩余的点是另外一组B。
每次找到一个点就把B组整体全部尝试松弛处理一次,再把B组最小距离的点加入A(关于B组距离最小的点就是确定了最小距离点的证明在例子后给出)。
举个栗子:
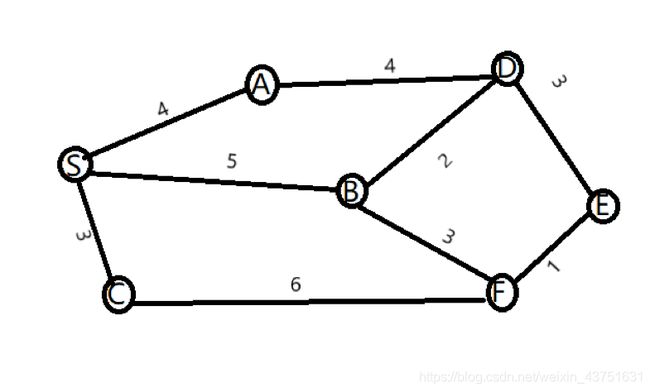
1)首先我们在不知道任何有关图的情况,我们只能当做所有点(除了 S S S)都无法到达 S S S,距离都为 ∞ { \infty } ∞。
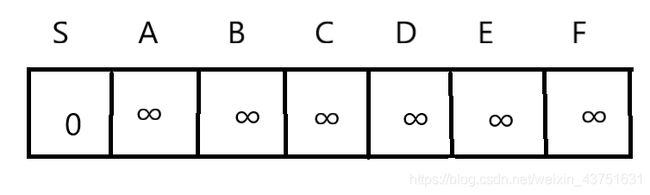
此时A组的元素为{S},B组{A,B,C,D,E,F}
2)更新B组内的元素距离
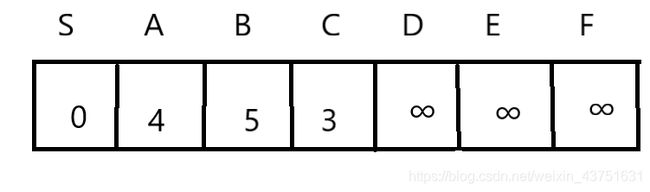
此时A内的元素为{S,C},B{A,B,D,E,F}。
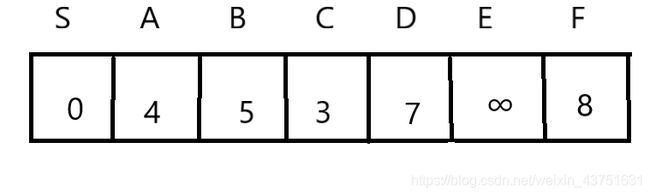
3)因为加入了C点,其他点距离可能会变化,更新B内元素距离
 A{S,C,A},B{B,D,E,F}
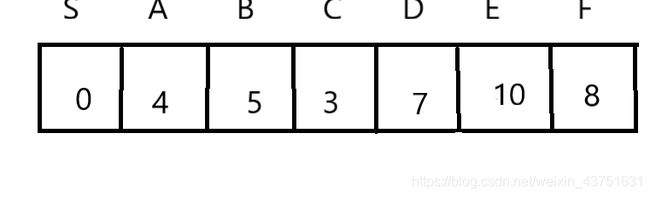
A{S,C,A},B{B,D,E,F}
到此为止,所有距离都求出来了了。
关于B组距离最小的点就是确定了最小距离的点的证明(叫说明更好):
首先我们明确一点,没有权值为负的边。也就是说,在更新后的B中最短的距离没有可能通过任何途径变得更短了(A内的松弛处理全部完成了),那么B组距离最小的点就是确定了最小距离的点。
这个说明也反映了为什么dijkstra算法只能处理没有负边的情况。
主要代码:
memset(vis, 0, sizeof(vis));
for(int i = 0; i < n; i++) dis[i] = (i==0 ? 0 : INF);
for(int i = 0; i < n; i++) {
int x, m = INF;
//如果y没有被加入集合A,且dis[y]是最小的,则把y加入集合A(用x = y实现)
for(int y = 0; y < n; y++)
if(!vis[y] && dis[y] <= m) m = dis[y], x = y;
vis[x] = 1; //标记新加入的点
//更新x相邻的点的dis[i]等同于更新所有点(不相邻距离为∞)
for(int y = 0; y < n; y++)
if(dis[y] > dis[x] + G[x][y])
dis[u] = dis[x] + G[x][y];
}
当然能看出来,朴素的dijkstra时间复杂度为 O ( V × E ) O(V\times E) O(V×E),如果 V V V和 E E E的乘积很大时就搞不定了。
此时就需要用堆来优化。
这里就不自己写堆了,使用STL的 p r i o r i t y _ q u e u e {priority\_ queue} priority_queue解决。
优先队列自动排序,队首元素就是新加入A的元素。
再用数组存对应点的边。时间复杂度可以降到 O ( V l o g V ) O(VlogV) O(VlogV)
再给优化算法代码之前,最好去了解一下链式向前星存图,不难,但是为了不让博客显得冗长,我不在这篇博客里面写了(万一哪天良心发现,又写一篇链式向前星呢)
主要dijkstra代码:
const long long INF = 0x3f3f3f3f3f3f3f3f;//视情况而定
int head[maxn],cnt = 0;
ll dis[maxn];
//---------------------------------->链式向前星
struct Edge{
int to;
int next;
int w;
}e[maxn];
void add(int x,int y,int w){
e[cnt] = {y,head[x],w};
head[x] = cnt++;
}
//------------------------------>
//------------------------------>堆优化的dijkstra
struct Node{
int p;
ll ds;
bool operator < (const Node&n)const{
return ds>n.ds;
}
};
void dijkstra(int s){
memset(dis,INF,sizeof(dis));
priority_queue<Node> q;
dis[s] = 0;
q.push({s,0});
while(!q.empty()){
int pp = q.top().p;
ll dds = q.top().ds;
q.pop();
if( dds != dis[pp] ) continue;
for(int i = head[pp];i >= 0;i = e[i].next){
int to = e[i].to;
int w = e[i].w;
if(dis[to] > dds + w){
dis[to] = dds + w;
q.push({to,dis[to]});
}
}
}
}
//------------------------------>