多项式乘法 快速傅里叶变换FFT

多项式的表示

系数表达

我们把一个次数界为n的多项式记为$A(x)=a[0]+a[1]x+a[2]x^2+a[3]x^3...$ ，其系数可以用一个一维向量$(a[0],a[1],a[2],a[3]...)$表示。

霍纳法则：
多项式A(x)可以化为:
$a[0]+x(a[1]+x(...x(a[n-1]+x)...)$，
O(n)的时间内得到多项式在x=x0处的值。

在进行多项式加法时，只需将对应项相加即可，即多项式A(x)加B(x)满足c[i]=a[i]+b[i]，所以加法的复杂度为O(n)，但是进行乘法或除法运算时，多项式A(x)中的每一项系数都需要和B(x)中的每一项系数相乘，并累加，因此复杂度不可避免的达到了O(n²)。

点值表达

对于一个次数界为n的多项式，可以用n个特殊的x及其对应多项式的值来表示，设$A(x[i])=y[i]$，
多项式A(x)可以表示为集合 { $(x[0],y[0]),(x[1],y[1]),(x[2],y[2]),...$ }，
其中x的取值各不相同。

通过点值表达集合确定多项式系数称为插值，该多项式称为插值多项式。
插值多项式唯一性： 对于任意n个点值对组成的集合{ $(x[0],y[0]),(x[1],y[1]),(x[2],y[2]),...(x[n-1],y[n-1])$ }，其中所有的$x[k]$都不同；那么存在唯一的次数界为n的多项式$A(x)$，满足$y[k]=A(x[k])，k=0,1,3...,n-1$。
证明：$y[k]=A(x[k])，k=0,1,3...,n-1$等价于以下矩阵方程

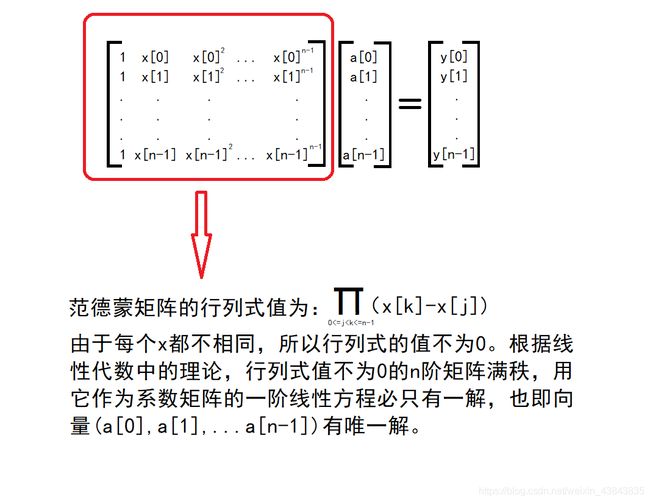
那么，为什么要用点值表达式呢？
从本质上讲，点值表达式刻画的是函数$f(x)=A(x)$，在x取不同值后形成的有序对集合，集合元素即为$<x,f(x)>$。那么对于两个函数f(x)和g(x)，它们在坐标上的加和，即为每处点值加和，h(x)=f(x)+g(x)，g(x)确定唯一的多项式。如果是乘积呢?同样，f(x)和g(x)的合成，即为每处点值的乘积，h(x)=f(x)*g(x)。这也就是使用点值表达式的优势，可以线性时间完成对两个多项式的乘积，结果以点值表达式的形式呈现。

基于单位复数根的FFT思路

通过以上对点值表达式的描述，快速多项式乘法已经有些许眉目了。关键的乘法步骤已经可以用O(n)的时间解决，剩下要处理的只剩下系数和点值之间的相互转换，以下将说明如何用O(nlgn)的时间处理这一问题。

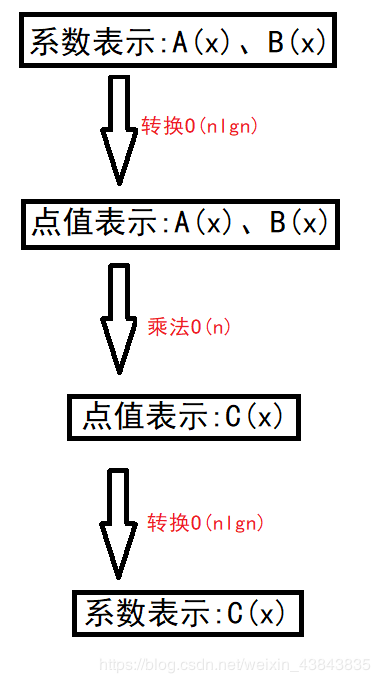
单位复数根的定义和性质

撇开不谈为什么引入单位复数根，先来说说单位复数根的定义和性质。

定义：

n次单位根是满足ωⁿ=1的复数ω，n次单位根恰好有n个：对于k=0，1，…n-1，这些根是e^2πik/n。
其中，e^iu定义为：e^iu=cos(u)+isin(u)，也就是说，单位根都位于坐标轴的单位圆上。
ω[n]=e^2πi/n称为主n次复数根，所有其他n次单位复数根都是ω[n]的幂次。

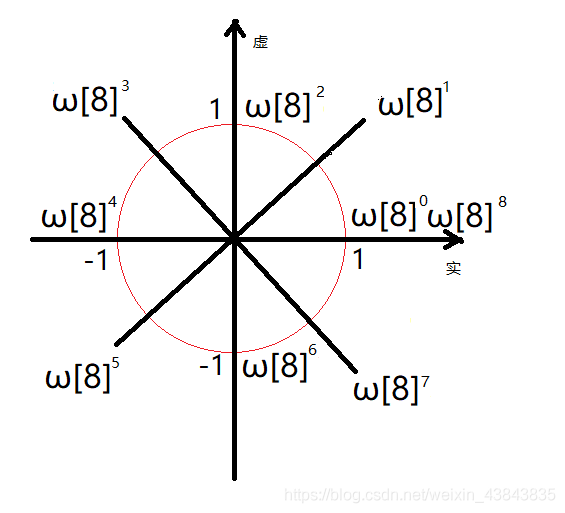
性质：

1.消去引理：
对于任何整数n>=0,k>=0,d>0，${\omega }_{dn}^{dk}=(e^{2\pi i/dn}{)}^{dk}=(e^{2\pi i/n}{)}^k={\omega }_n^k$

2.折半引理：
如果n>0位偶数，那么n个n次单位复数根的平方的集合就是n/2个n/2次单位复数根的集合。
也即，$({\omega }_n^{k+n/2}{)}^2={\omega }_n^{2k+n}={\omega }_n^{2k}{\omega }_n^n={\omega }_n^{2k}=({\omega }_n^k{)}^2$

3.求和引理：
对任意整数n>=1和不能被n整除的非负数k，有 ${\sum }_{j=0}^{n-1}({\omega }_n^k{)}^j=0$

快速傅里叶变换（FFT）

在分析出单位复数根的折半引理时，FFT的本质也逐渐显露，即分治。为了方便计算，n取2的次方。

系数表达式转换成点值表达式(FFT)：
原多项式等于两个新的多项式加和，

$A(x)=A^0(x^2)+x{A}^1(x^2)$，

其中$A^0(x)=a[0]+a[2]x+a[4]x^2...，A^1(x)=a[1]+a[3]x+a[5]x^2...$

于是，向A⁰(x)和A¹(x)中代入单位根，$({\omega }_n^0{)}^2,({\omega }_n^1{)}^2,...,({\omega }_n^{n-1}{)}^2$，根据折半引理，实际上只有n/2个不同的单位根组成。什么意思呢？现在有n个需要代入的单位根，但是我们只需要代入前面n/2个，算出A⁰(x)和A¹(x)，就能同时得出两项A(x)的结果。
对于两个新的多项式，同拆解A(x)时步骤一样，每个多项式又可以拆解成两个，不断向下拆解，直到n为1时，返回一个常数项，回溯累加，得出点值表达式。

点值表达式转换成系数表达式(IFFT)：
在FFT过程中，点值通解$y[j]={\sum }_{k=0}^{n-1}a[k]{\omega }_n^{kj}$，把它写成矩阵乘法形式(如上文所示)。
代入${\omega }_n$的幂次，解出系数的通解 $a[j]=1/n{\sum }_{k=0}^{n-1}y[k]{\omega }_n^{-kj}$,
我们发现两式具有相同的结构，转换成点值可以由FFT计算，则转换成系数也可以由FFT计算，且时间消耗是相等的。

FFT的高效实现

上文描述的FFT已经足够高效了，但是递归的往往会带来常数过大的后果，FFT还有一个更高效的迭代实现。
在递归中，我们把一个多项式分成两个多项式，一直到把它分成n个系数才开始返回计算。例如一个系数为a[0]到a[7]的多项式最终n个常数项按时间序从早到晚排序的下标为0,4,2,6,1,5,3,7.

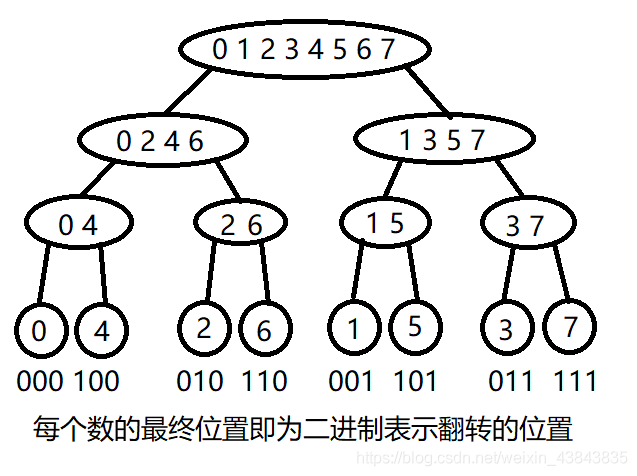
因此可以用一个循环，在O(n)的时间内找到每个元素的位置，这样就省去了递归时函数调用的时间开销。

FFT模板：
（输入两个多项式各项的系数，按次数从小到大。输出各项系数）

#include 
#include 
#include 
#include 
#include 
#include  
using namespace std;

const int INF = 0X7FFFFFFF;
const int MAXN = 1000000;
const double pi = acos(-1);
int rev[MAXN];
string num1;
string num2;
complex<double> in1[MAXN];
complex<double> in2[MAXN];
int ans[MAXN];

inline void FFT( complex<double> *a, int mark, int n ){
	int bit = 0;
	while((1<<bit)<n) ++bit;
	//-------------------------------------------------//
	//找到每个系数的位置
	for(int i=0;i<n;++i){
		rev[i] = (rev[i>>1]>>1)|((i&1)<<(bit-1));
		//记着就好QAQ
		if( i<rev[i] ){
			swap(a[i],a[rev[i]]);
			//保证不重复交换
		}
	}
	//-------------------------------------------------//
	//迭代FFT
	for(int cnt=1;cnt<n;cnt*=2){
		complex<double> t(cos(pi/cnt),mark*sin(pi/cnt));//µ¥Î»¸ù 
		for(int i=0;i<n;i+=cnt*2){
			complex<double> omg(1,0);
			for(int j=0; j<cnt; ++j,omg*=t){
				complex<double> x = a[i+j];
				complex<double> y = omg*a[i+j+cnt];
				a[i+j] = x+y;
				a[i+j+cnt] = x-y;
			} 
		} 
	}
	//-------------------------------------------------//
} 

int main(){
	cin>>num1>>num2;
	int l1=num1.length();
	int l2=num2.length();
	for(int i=0;i<l1;++i){
		in1[i] = num1[i]-'0';
		cout<<in1[i].real()<<" ";
	}
	cout<<endl;
	for(int i=0;i<l2;++i){
		in2[i] = num2[i]-'0';
		cout<<in2[i].real()<<" ";
	}
	cout<<endl;
	int maxl = max(l1,l2);
	int bit = 0;
	while((1<<bit)<maxl) ++bit;
	maxl = 1<<(bit+1);
	FFT(in1,1,maxl);
	FFT(in2,1,maxl);
	for(int i=0;i<maxl;++i){
		in1[i] *= in2[i];
	}
	FFT(in1,-1,maxl);
	for(int i=0;i<maxl;++i){
		ans[i] = (int)(in1[i].real()/maxl+0.5);
	}
	int flag = INF;
	for(int i=maxl-1;i>=0;--i){
		if(ans[i]!=0){
			flag = i;
			break;
		}
	}
	if(flag==INF){
		cout<<0<<endl;
	}else{
		for(int i=0;i<=flag;++i){
			cout<<ans[i]<<" ";
		}
	}
	return 0;
}