二叉树和二叉排序树的操作

二叉树和二叉排序树的操作

参考书籍-王道-书籍结构-代码已在vs2019验证过!

1.二叉树的遍历

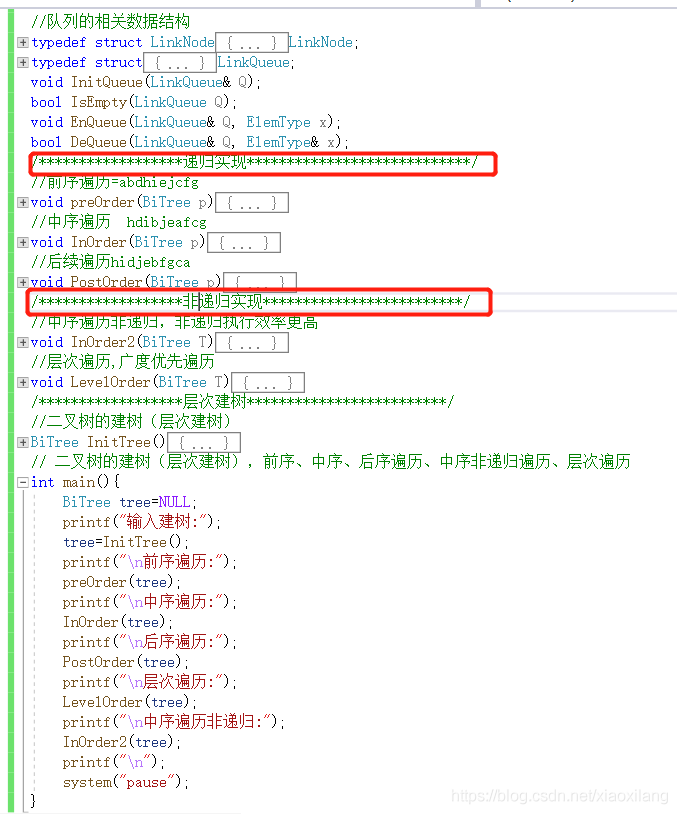
二叉树的建树（层次建树），前序、中序、后序遍历、中序非递归遍历、层次遍历

#include 
typedef char BiElemType;
typedef struct BiTNode {
	BiElemType c;//c就是书籍上的data
	struct BiTNode* lchild;
	struct BiTNode* rchild;
}BiTNode, * BiTree;

typedef struct tag {
	BiTree p;
	struct tag* pnext;
}tag_t, * ptag_t;

//栈的相关数据结构
#define MaxSize 50
typedef BiTree ElemType;
typedef struct {
	ElemType data[MaxSize];
	int top;
}SqStack;
void InitStack(SqStack& S);
bool StackEmpty(SqStack& S);
bool Push(SqStack& S, ElemType x);
bool Pop(SqStack& S, ElemType& x);
bool GetTop(SqStack& S, ElemType& x);
//队列的相关数据结构
typedef struct LinkNode {
	ElemType data;
	struct LinkNode* next;
}LinkNode;
typedef struct {
	LinkNode* front, * rear;
}LinkQueue;
void InitQueue(LinkQueue& Q);
bool IsEmpty(LinkQueue Q);
void EnQueue(LinkQueue& Q, ElemType x);
bool DeQueue(LinkQueue& Q, ElemType& x);
/******************递归实现****************************/
//前序遍历=abdhiejcfg
void preOrder(BiTree p)
{
	if (p != NULL)
	{
		putchar(p->c);//等价于visit函数
		preOrder(p->lchild);
		preOrder(p->rchild);
	}
}
//中序遍历  hdibjeafcg
void InOrder(BiTree p)
{
	if (p != NULL)
	{
		InOrder(p->lchild);
		putchar(p->c);
		InOrder(p->rchild);
	}
}
//后续遍历hidjebfgca
void PostOrder(BiTree p)
{
	if (p != NULL)
	{
		PostOrder(p->lchild);
		PostOrder(p->rchild);
		putchar(p->c);
	}
}
/******************非递归实现*************************/
//中序遍历非递归，非递归执行效率更高
void InOrder2(BiTree T)
{
	SqStack S;
	InitStack(S); BiTree p = T;
	while (p || !StackEmpty(S))//逻辑或||
	{
		if (p)
		{
			Push(S, p);
			p = p->lchild;
		}
		else {
			Pop(S, p); putchar(p->c);
			p = p->rchild;
		}
	}
}
//层次遍历,广度优先遍历
void LevelOrder(BiTree T)
{
	LinkQueue Q;
	InitQueue(Q);
	BiTree p;
	EnQueue(Q, T);//树根入队
	while (!IsEmpty(Q))
	{
		DeQueue(Q, p);
		putchar(p->c);
		if (p->lchild != NULL)
			EnQueue(Q, p->lchild);
		if (p->rchild != NULL)
			EnQueue(Q, p->rchild);
	}
}
/******************层次建树*************************/
//二叉树的建树（层次建树）
BiTree InitTree()
{
	BiTree pnew;
	int i, j, pos;
	char c;
	BiTree tree = NULL;//树根
	ptag_t phead = NULL, ptail = NULL, listpnew, pcur=NULL;
	//abcdefghij
	while (scanf_s("%c", &c) != EOF)
	{
		if (c == '\n')
		{
			break;
		}
		pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc申请空间并对空间进行初始化，赋值为0
		pnew->c = c;
		listpnew = (ptag_t)calloc(1, sizeof(tag_t));
		listpnew->p = pnew;
		if (NULL == tree)
		{
			tree = pnew;//树的根
			phead = listpnew;//链表头
			ptail = listpnew;//链表尾
			pcur = listpnew;
			continue;
		}
		else {
			ptail->pnext = listpnew;//新结点放入链表，通过尾插法
			ptail = listpnew;
		}
		if (NULL == pcur->p->lchild)
		{
			pcur->p->lchild = pnew;
		}
		else if (NULL == pcur->p->rchild)
		{
			pcur->p->rchild = pnew;
			pcur = pcur->pnext;
		}
	}
	return tree;
}
// 二叉树的建树（层次建树），前序、中序、后序遍历、中序非递归遍历、层次遍历
int main(){
	BiTree tree=NULL;
	printf("输入建树:");
	tree=InitTree();
	printf("\n前序遍历:");
	preOrder(tree);
	printf("\n中序遍历:");
	InOrder(tree);
	printf("\n后序遍历:");
	PostOrder(tree);
	printf("\n层次遍历:");
	LevelOrder(tree);
	printf("\n中序遍历非递归:");
	InOrder2(tree);
	printf("\n");
	system("pause");
}

2.二叉排序树

二叉排序树的遍历和搜索

#include 
#include 
typedef int KeyType;
typedef struct BSTNode {
	KeyType key;
	struct BSTNode* lchild, * rchild;
}BSTNode, * BiTree;

int BST_Insert(BiTree& T, KeyType k)
{
	if (NULL == T)
	{
		T = (BiTree)malloc(sizeof(BSTNode));
		T->key = k;
		T->lchild = T->rchild = NULL;
		return 1;
	}
	else if (k == T->key)
		return 0;
	else if (k < T->key)
		return BST_Insert(T->lchild, k);
	else
		return BST_Insert(T->rchild, k);
}

void Creat_BST(BiTree& T, KeyType str[], int n)
{
	T = NULL;
	int i = 0;
	while (i < n)
	{
		BST_Insert(T, str[i]);
		i++;
	}
}
//递归算法简单，但执行效率较低，实现留给大家编写
BSTNode* BST_Search(BiTree T, KeyType key, BiTree& p)
{
	p = NULL;
	while (T != NULL && key != T->key)
	{
		p = T;
		if (key < T->key) T = T->lchild;
		else T = T->rchild;
	}
	return T;
}
//这个书上没有
void DeleteNode(BiTree& root, KeyType x) {
	if (root == NULL) {
		return;
	}
	if (root->key > x) {
		DeleteNode(root->lchild, x);
	}
	else if (root->key < x) {
		DeleteNode(root->rchild, x);
	}
	else { //查找到了删除节点
		if (root->lchild == NULL) { //左子树为空
			BiTree tempNode = root;
			root = root->rchild;
			free(tempNode);
		}
		else if (root->rchild == NULL) { //右子树为空
			BiTree tempNode = root;
			root = root->lchild;
			free(tempNode);
		}
		else {//左右子树都不为空
		   //一般的删除策略是左子树的最大数据 或 右子树的最小数据 代替该节点(这里采用查找左子树最大数据来代替)
			BiTree tempNode = root->lchild;
			while (tempNode->rchild != NULL) {
				tempNode = tempNode->rchild;
			}
			root->key = tempNode->key;
			DeleteNode(root->lchild, tempNode->key);
		}
	}
}

void InOrder(BiTree T)
{
	if (T != NULL)
	{
		InOrder(T->lchild);
		printf("%3d", T->key);
		InOrder(T->rchild);
	}
}
int main()
{
	BiTree T;
	BiTree parent;
	BiTree search;
	KeyType str[] = { 54,20,66,41,28,79,58 };
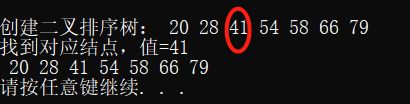
	printf("\n创建二叉排序树：");
	Creat_BST(T, str, 7);
	InOrder(T);
	printf("\n");
	search = BST_Search(T, 41, parent);
	if (search)
	{
		printf("找到对应结点，值=%d\n", search->key);
	}
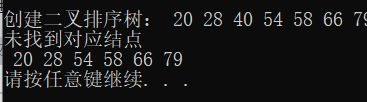
	else {
		printf("未找到对应结点\n");
	}
	DeleteNode(T, 40);
	InOrder(T);
	printf("\n");
	system("pause");
}