二叉树 - 表达式二叉树（C语言）

问题描述：

表达式可以用表达式二叉树来表示。对于简单的四则运算表达式，请实现以下功能。

 （1）对于任意给出的前缀表达式（不带括号）、中缀表达式（可以带括号）或后缀表达式（不带括号），能够在计算机内部构造出一颗表达式二叉树，并且以图示显示出来（字符图或图形的形式）。

 （2）对于构造好的内部表达式二叉树、按照用户的要求，输出相应的前缀表达式（不带括号）、中缀表达式（可以带括号，但不允许冗余括号）或后缀表达式（不带括号）

相关知识点：

1.后缀表达式的特点是：一定以两个操作数开始，且以操作符结尾，形如“a b + c d e + * *”就是一个后缀表达式

2.表达式树的特点就是：树的树叶是操作数（常数或变量），而其他节点为操作符。由于一般的操作符都是二元的，所以表达式树一般的都是二叉树。

3.中缀表达式建树过程：代码中InTree（）为递归函数、有三个参数、s - 字符串的首地址，i和j分别为子串起始位置和终止位置。如果i == j，说明子串只有一个字符，即为叶子节点，则创建只有一个根节点的二叉树并返回之。如果i != j，根据运算规则（先乘除后加减），在串中找‘+’和‘-’，以最后的‘+’或‘-’为根（体现从左到右的原则）；如果没有‘+’或‘-’时，则进一步找‘*’或’/‘（体现先乘除后加减），同样以最后的运算符为根，将串分为两部分，即左子树和右子树。创建一个根节点，将找到的运算符放入，递归调用自身进入左子树的建树过程，之后递归调用自身进入右子树的建树过程。

5.树的遍三种遍历分别是先序遍历、中序遍历与后序遍历，正好对应表达式的三种形式：前缀型、中缀型与后缀型，其中前缀和后缀表达式最大的优点就是不需要括号来表明优先级。

4.1后缀表达式建树过程：我们一次一个符号地读入表达式。如果符号是操作数，那么就建立一个单结点树并将它推入栈中。如果符号是操作符，那么就从栈中弹出两棵树T1和T2(T1先弹出)并形成一棵新的树，该树的根就是操作符，它的左、右儿子分别是T2和T1。然后将指向这颗树的指针压入栈中。

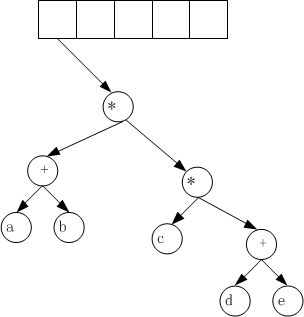
4.2 后缀表达式建树过程图示如下：

（图片来源：https://blog.csdn.net/qq_26849233/article/details/72910010）

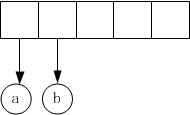
  如“a b + c d e + * *”生成表达式树的主要过程如下图所示：

（1）依次读入操作数a 和 b，并压入栈中

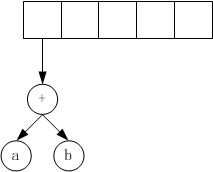
（2）遇到操作符“+”

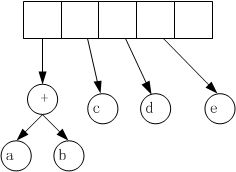
（3）遇到c  d   e 操作数

（4）遇到“+”操作符

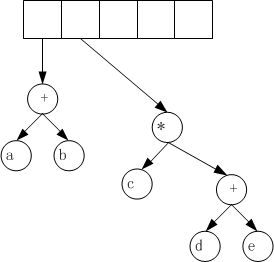
（5）遇到“*”操作符

（6）遇到“*”操作符

完整代码如下：

/* 表达式二叉树 */

//#include "stdafx.h"
//博客地址：https://blog.csdn.net/y_16041527
#include "btree.cpp"      //该头文件为我自定义的头文件，其中的函数的声明和实现在我的博客中有 
#include 

//函数声明
bitree InTree(char s[], int i, int j);     //中缀表达式建树过程    
bitree PosTree(char s[], int len );        //后缀表达式建树过程
bitree PerTree(char s[], int len );        //前缀表达式建树过程


//前缀表达式建树过程 - 由于操作数在叶节点位置和前缀表达式的特点，其建树过程与后缀表达式一致，只不过扫描方向正好相反 
bitree PerTree(char s[], int len)
{
	//	cout << "len：" << len << endl;
	//计数变量 
	int i;    
	bitree p, root;
	//临时栈 - 用来存放指向树节点的指针
	struct stack
	{
		bitnode *vec[MaxSize];
		int top;
	} ;
	struct stack q;
	q.top = 0;
	
	//遍历字符串，若为操作数 - 则生成根节点并将指向该根节点的指针入栈、若为运算符 - 则生成节点并在临时栈中弹出两个指向操作数
	//节点的指针，并指向该运算符节点并将其入栈
	for( i = len-1; i >= 0; i-- )
	{
		//为操作符 
		if( s[i] == '+' || s[i] == '/' || s[i] == '*' || s[i] == '-' )
		{
			p = (bitree)malloc(sizeof(bitnode));
			p->data = s[i];
			p->left = q.vec[q.top--];    //先弹出的为左节点 
			p->right = q.vec[q.top--];     //后弹出的为右节点 
			q.vec[++q.top] = p;           //将根节点入栈 
		}
		else
		{
			//s[i]为操作数 
			p = (bitree)malloc(sizeof(bitnode));
			p->data = s[i];
			p->left = NULL;
			p->right = NULL;
			q.vec[++q.top] = p;      //将指向操作数节点的指针入栈 
		}
	} 
	
	root = q.vec[q.top--];        //这一步很关键，因为该二叉树的根节点最后被保留在了栈中 
	return root;
} 


//中缀表达式建树过程  - 递归过程 
bitree InTree(char s[], int i, int j)  //s - 表达式字符串、i - 字符串起始位置、j - 字符串最后一个字符的位置 
{
	//动态生成的树节点 
	bitree p;
	int k, flag = 0, pos;

	//如果i == j，则说明字符串只有一个字符，即为叶子节点、则创建只有一个根节点的二叉树并返回
	if (i == j)
	{
		p = (bitree)malloc(sizeof(bitnode));
		p->data = s[i];
		p->left = NULL;
		p->right = NULL;
		return p;
	}
	//以下是 i != j的情况
	//从左往右找最后一个+或-，先找+或-为了体现先乘除后加减的原则 
	for (k = i; k <= j; k++)
	{
		if (s[k] == '+' || s[k] == '-')
		{
			flag = 1;
			pos = k;
		}
	}
	//若没有+或-，则寻找字符串中最后一个*或/ 
	if (flag == 0)
	{
		for (k = 0; k <= j; k++)
		{
			if (s[k] == '*' || s[k] == '/')
			{
				flag = 1;
				pos = k;
			}
		}
	}
	//若flag不等于0，则以pos为界将字符串分为左右两部分，分别对应表达式二叉树的左、右子树 
	//同样以最后的运算符为根，将串分为两部分
	//创建一个根节点、将找到的运算符放入 
	if (flag != 0)
	{
		p = (bitree)malloc(sizeof(bitnode));
		p->data = s[pos];
		p->left = InTree(s, i, pos - 1);      //递归调用自身进入其左子树建树过程 
		p->right = InTree(s, pos + 1, j);     //递归调用自身进入其右子树建树过程 
		return p;
	}
	else
		return NULL;
}

//后缀表达式建树过程
bitree PosTree(char s[], int len)
{
//	cout << "len：" << len << endl;
	//计数变量 
	int i;    
	bitree p, root;
	//临时栈 - 用来存放指向树节点的指针
	struct stack
	{
		bitnode *vec[MaxSize];
		int top;
	} ;
	struct stack q;
	q.top = 0;
	
	//遍历字符串，若为操作数 - 则生成根节点并将指向该根节点的指针入栈、若为运算符 - 则生成节点并在临时栈中弹出两个指向操作数
	//节点的指针，并指向该运算符节点并将其入栈
	for( i = 0; i < 9; i++ )
	{
		//为操作符 
		if( s[i] == '+' || s[i] == '/' || s[i] == '*' || s[i] == '-' )
		{
			p = (bitree)malloc(sizeof(bitnode));
			p->data = s[i];
			p->right = q.vec[q.top--];    //先弹出的为右节点 
			p->left = q.vec[q.top--];     //后弹出的为左节点 
			q.vec[++q.top] = p;           //将根节点入栈 
		}
		else
		{
			//s[i]为操作数 
			p = (bitree)malloc(sizeof(bitnode));
			p->data = s[i];
			p->left = NULL;
			p->right = NULL;
			q.vec[++q.top] = p;      //将指向操作数节点的指针入栈 
		}
	} 
	
	root = q.vec[q.top--];        //这一步很关键，因为该二叉树的根节点最后被保留在了栈中 
	return root;
} 

int main()
{
	bitree root;
	char s[MaxSize];
	cout << "中缀表达式:";
	cin >> s;

	root = InTree(s, 0, strlen(s) - 1);
	cout << "表达式二叉树" << endl;
	DispTree(root);
	cout << endl;
	
	cout << "该表达式二叉树三种遍历" << endl;
	cout << "前序遍历:";
	PerOrder(root);
	cout << endl;
	cout << "中序遍历:";
	InOrder(root);
	cout << endl;
	cout << "后序遍历:";
	PostOrder(root);
	cout << endl;
		
	cout << "后缀表达式:";
	cin >> s;
	root = PosTree(s,strlen(s));
	cout << "表达式二叉树" << endl;
	DispTree(root);
	cout << endl;
	
	cout << "前缀表达式:";
	cin >> s;
	root = PerTree(s,strlen(s));
	cout << "表达式二叉树" << endl;
	DispTree(root);
	cout << endl;
	
	root = FreeTree(root);
	if (root == NULL)
		cout << "释放成功" << endl;

	return 0;
}

运行结果：

中缀表达式:a+b*c-e/f
表达式二叉树
    - (r)------------------
        + (0)----------------
            a (0)--------------
            * (1)--------------
                b (0)------------
                c (1)------------
        / (1)----------------
            e (0)--------------
            f (1)--------------

该表达式二叉树三种遍历
前序遍历:- + a * b c / e f
中序遍历:a + b * c - e / f
后序遍历:a b c * + e f / -
后缀表达式:abc*+ef/-
表达式二叉树
    - (r)------------------
        + (0)----------------
            a (0)--------------
            * (1)--------------
                b (0)------------
                c (1)------------
        / (1)----------------
            e (0)--------------
            f (1)--------------

前缀表达式:-+a*bc/ef
表达式二叉树
    - (r)------------------
        + (0)----------------
            a (0)--------------
            * (1)--------------
                b (0)------------
                c (1)------------
        / (1)----------------
            e (0)--------------
            f (1)--------------

释放成功

--------------------------------
Process exited after 30.01 seconds with return value 0
请按任意键继续. . .