图——无向图，深度优先搜索，广度优先搜索，路径查找

定义：图是由一组顶点和能够将两个顶点连接起来的边构成的。
无向图：边只连接两个顶点，没有其他含义。
有向图：边不仅仅连接两个顶点，并且具有方向。
图的存储结构
①邻接矩阵

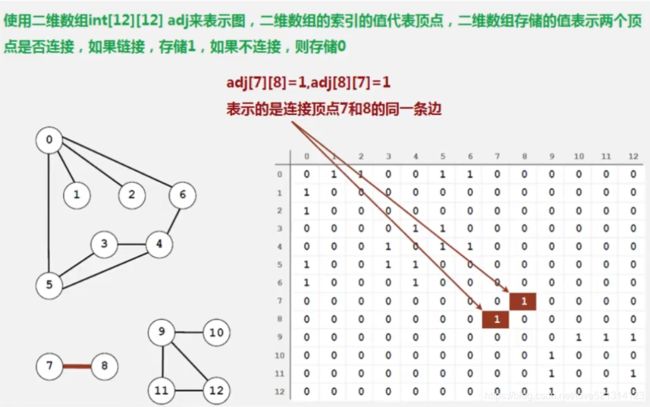
很明显，邻接矩阵的空间复杂度是平方级别的，当处理问题规模较大的时候，内存可能不够用。

②邻接表

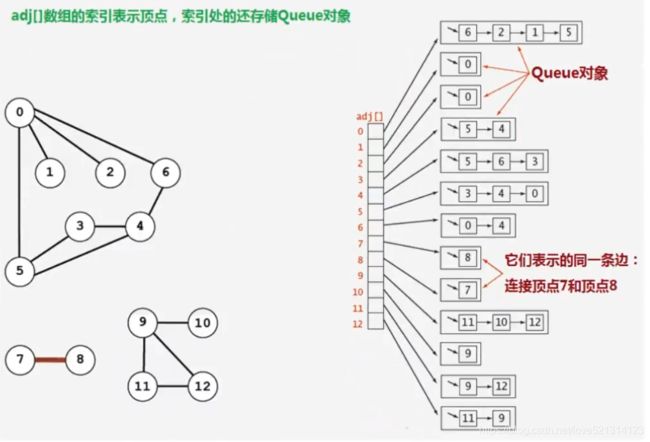
邻接表的空间复杂度比邻接矩阵小得多，因此以后就用邻接表的存储形式来存储图。

接下来用代码来实现图

构造方法

 //顶点数目
    private final int V;
    //边的数目
    private int E;
    //邻接表
    private Queue<Integer>[] adj;
    public Graph(int V) {
        this.V = V;
        this.E = 0;
        this.adj = new Queue[V];
        //默认情况下，Queue存储的为空
        for (int i = 0; i < adj.length; i++) {
            adj[i]=new Queue<Integer>();
        }
    }

向图中添加一条边

 public void addEdge(int v,int w){
        adj[v].enqueue(w);
        adj[w].enqueue(v);
        //边的数量加一
        E++;
    }

获取和顶点v相邻的所有顶点

public Queue<Integer> adj(int v){
         return adj[v];
    }

无向图完整代码

public class Graph {
    //顶点数目
    private final int V;
    //边的数目
    private int E;
    //邻接表
    private Queue<Integer>[] adj;
    public Graph(int V) {
        this.V = V;
        this.E = E;
        this.adj = new Queue[V];
        for (int i = 0; i < adj.length; i++) {
            adj[i]=new Queue<Integer>();
        }
    }
    //获取顶点数目
    public int getV(){
        return  V;
    }
    //获取边的数目
    public int getE(){
        return E;
    }
    //向图中添加一条边
    public void addEdge(int v,int w){
        adj[v].enqueue(w);
        adj[w].enqueue(v);
        //边的数量加一
        E++;
    }
    //获取和顶点v相邻的所有顶点
    public Queue<Integer> adj(int v){
         return adj[v];
    }
}

深度优先搜索
含义：在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，再找兄弟结点。

找出G图中所有与v相通的顶点

public void dfs(Graph G,int v){
        //把v顶点标示为已搜索
        marked[v]=true;
        for (Integer w : G.adj(v)) {
            //判断w顶点是否被搜索过，如果没有，则递归调用进行深度搜索
            if (!marked[w]){
                dfs(G,w);
            }
        }
        //相通数量+1
        count++;
    }

深度优先搜索完整代码

public class DepthFirstSearch {
    //索引代表顶点，值代表是否被搜索过
    private boolean[] marked;
    //记录有多少顶点与s相同
    private int count;
    public DepthFirstSearch(Graph G,int s){
        this.marked=new boolean[G.getV()];
        this.count=0;
        dfs(G,s);
    }
    //找出G图中所有与v相通的顶点
    public void dfs(Graph G,int v){
        //把v顶点标示为已搜索
        marked[v]=true;
        for (Integer w : G.adj(v)) {
            //判断w顶点是否被搜索过，如果没有，则递归调用进行深度搜索
            if (!marked[w]){
                dfs(G,w);
            }
        }
        //相通数量+1
        count++;
    }
    //判断w顶点是否与v顶点相通
    public boolean marked(int w){
        return marked[w];
    }
    //获取与顶点s相通的所有顶点的总数
    public int getCount(){
        return count;
    }
}

广度优先搜索
含义：在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，再找子结点。

找出G图中所有与v相通的顶点

public void bfs(Graph G,int v){
        //把v顶点标示为已搜索
        marked[v]=true;
        //让v进入队列，待搜索
        waitSearch.enqueue(v);
        //通过循环，如果队列不为空，则从队列中弹出一个元素进行搜索
        while (!waitSearch.isEmpty()){
            Integer wait = waitSearch.dequeue();
            //遍历wait的邻接表
            for (Integer w : G.adj(wait)) {
                if (!marked(w)){
                    bfs(G,w);
                }
            }
        }
        //相通数量+1
        count++;
    }

广度优先搜索完整代码

public class BreadFirstSearch {
    //索引代表顶点，值代表是否被搜索过
    private boolean[] marked;
    //记录有多少顶点与s相通
    private int count;
    //用来搜索待存储邻接表的点
    private Queue<Integer> waitSearch;
    public BreadFirstSearch(Graph G, int s){
        this.marked=new boolean[G.getV()];
        this.count=0;
        this.waitSearch=new Queue<Integer>();
        bfs(G,s);
    }
    //找出G图中所有与v相通的顶点
    public void bfs(Graph G,int v){
        //把v顶点标示为已搜索
        marked[v]=true;
        //让v进入队列，待搜索
        waitSearch.enqueue(v);
        //通过循环，如果队列不为空，则从队列中弹出一个元素进行搜索
        while (!waitSearch.isEmpty()){
            Integer wait = waitSearch.dequeue();
            //遍历wait的邻接表
            for (Integer w : G.adj(wait)) {
                if (!marked(w)){
                    bfs(G,w);
                }
            }
        }
        //相通数量+1
        count++;
    }
    //判断w顶点是否与v顶点相通
    public boolean marked(int w){
        return marked[w];
    }
    //获取与顶点s相通的所有顶点的总数
    public int getCount(){
        return count;
    }
}

路径查找
在日常生活中，我们通常会使用地图软件进行导航，将路线显示出来。应用在图中转换成，判断s顶点到v顶点之间是否存在一条路径相通，如果有，请找出。（注：只需找到一条即可）
实现路径查找的关键是创建一个辅助数组，它的索引代表顶点，值代表从起点s到当前顶点路上的最后一个顶点，如图所示：

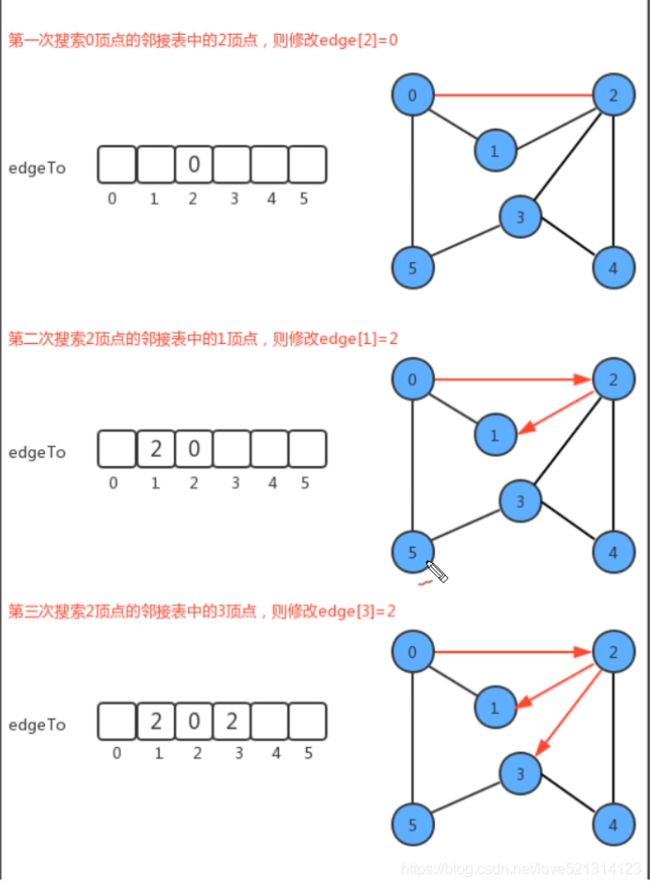
构造方法

//索引代表顶点，值代表当前顶点是否被搜索过
    private boolean[] marked;
    //起点
    private int s;
    //索引代表顶点，值代表从起点s到当前顶点路上的最后一个顶点
    private int[] edgeTo;
    public DepthFirstPaths(Graph G,int s){
        this.marked=new boolean[G.getV()];
        this.s=s;
        this.edgeTo=new int[G.getV()];
        dfs(G,s);
    }

找出s到v的路径

 public Stack<Integer> pathTo(int w){
        if (!hasPath(w)){
            return null;
        }
        //创建一个栈对象，保存路径中的所有顶点
        Stack<Integer> path = new Stack<>();
        //通过循环，从顶点v开始，找到起点为止
        for (int i=w;i!=s;i=edgeTo[i]){
            path.push(i);
        }
        //把起点放入栈中
        path.push(s);
        return path;
    }

路径查找完整代码

public class DepthFirstPaths {
    //索引代表顶点，值代表当前顶点是否被搜索过
    private boolean[] marked;
    //起点
    private int s;
    //索引代表顶点，值代表从起点s到当前顶点路上的最后一个顶点
    private int[] edgeTo;
    public DepthFirstPaths(Graph G,int s){
        this.marked=new boolean[G.getV()];
        this.s=s;
        this.edgeTo=new int[G.getV()];
        dfs(G,s);
    }
    //找出G图中所有与v相通的顶点
    public void dfs(Graph G,int v){
        //把v顶点标示为已搜索
        marked[v]=true;
        for (Integer w : G.adj(v)) {
            //判断w顶点是否被搜索过，如果没有，则递归调用进行深度搜索
            if (!marked[w]){
                edgeTo[w]=v;
                dfs(G,w);
            }
        }
    }
    //判断w和s是否存在路径
    public boolean hasPath(int w){
        return marked[w];
    }
    //找出s到v的路径
    public Stack<Integer> pathTo(int w){
        if (!hasPath(w)){
            return null;
        }
        //创建一个栈对象，保存路径中的所有顶点
        Stack<Integer> path = new Stack<>();
        //通过循环，从顶点v开始，找到起点为止
        for (int i=w;i!=s;i=edgeTo[i]){
            path.push(i);
        }
        //把起点放入栈中
        path.push(s);
        return path;
    }
}

b站详细讲解网址：http://yun.itheima.com/course/639.html