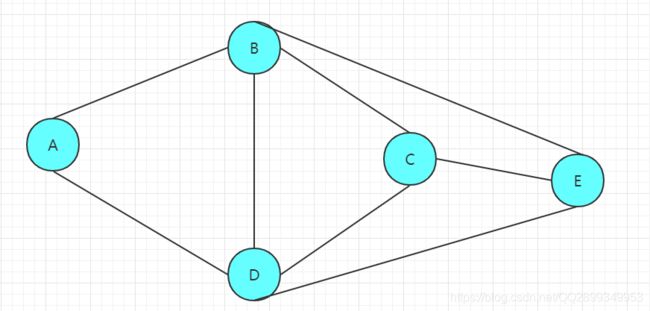
图 —— 最小生成树
目录
- 一、普利姆算法
- 1、无权图的最小生成树
- 2、带权图的最小生成树
- 1、无向带权图的最小生成树
- 2、有向带权图的最小生成树
- 二、克鲁斯卡尔
注意:
最小生成树和最短路径不一样的,实际应用中就是:最小生成树求的是经过所有城市的最短的那条路,最短路径只是求两个城市之间最短的那条路,它并不经过所有城市!
算图的最小生成树有两种算法,一种是普利姆算法,还有一种是克鲁斯卡尔算法,普利姆算法的好处是可以指定起点,克鲁斯卡尔算法的好处是它找出来的最小生成树肯定是那个最小的最小生成树;
申明:图是偷的这个博主的 → 最小生成树之java实现
一、普利姆算法
算法思想:
- 取图中任意一个顶点v作为生成树的根
- 选择一个顶点在生成树中,另一个顶点不在生成树中的边权最小的边,将顶点以及边添加至生成树中
- 继续执行步骤2,直至生成树上含有n-1条边为止
1、无权图的最小生成树
无权的实现很简单:
随便从一个顶点开始找一个经过所有节点的路径即可;
下面的代码也是基于深度优先搜索实现的:
/**
* @ClassName Node
* @Description 图节点
* @Author lzq
* @Date 2019/6/19 04:39
* @Version 1.0
**/
public class Node {
public char label; //存放的数据
public boolean wasVisited; //记录有无被访问过
public Node(char label) {
this.label = label;
this.wasVisited = false;
}
}
import java.util.Stack;
/**
* @ClassName Graph2
* @Description 图——最小生成树
* @Author lzq
* @Date 2019/6/19 06:01
* @Version 1.0
**/
public class Graph {
private final int MAX_VERTS = 20; //表示一个图节点能连接的最大定点数
private Node[] nodeList; //顶点数组
private int[][] adjMal; //邻接矩阵,用来存方节点之间关系的
private int nNode; //当前顶点数量
private Stack stack; //深度优先遍历需要用到
public Graph() {
nodeList = new Node[MAX_VERTS];
adjMal = new int[MAX_VERTS][MAX_VERTS];
nNode = 0;
for (int i = 0; i < MAX_VERTS; i++) {
for (int j = 0; j < MAX_VERTS; j++) {
adjMal[i][j] = 0;
}
}
stack = new Stack<>();
}
/**
* 添加节点
* @param lab
*/
public void addNode(char lab) {
nodeList[nNode++] = new Node(lab);
}
/**
* 添加边
* @param start
* @param end
*/
public void addEdge(int start,int end) {
adjMal[start][end] = 1;
adjMal[end][start] = 1;
}
/**
* 打印
* @param v
*/
public void displayNode(int v) {
System.out.print(nodeList[v].label);
}
/**
* 最小生成树
*/
public void mxt() {
//默认从顶点中的第一个节点开始
nodeList[0].wasVisited = true;
stack.push(0);
while (!stack.empty()) {
int c = stack.peek();
int v = getAdjUnvisiteNode(c);
if(v == -1) { //没有找到邻接的没有访问的节点
stack.pop();
}else {
nodeList[v].wasVisited = true;
stack.push(v);
displayNode(c); //起点
System.out.print("-->");
displayNode(v); //终点
System.out.print("\t");
}
}
//到这所有的节点都访问玩了,需要把访问状态改回去
for (int i = 0; i < nNode; i++) {
nodeList[i].wasVisited = false;
}
}
/**
* 找到指定节点邻接的未被访问的节点
* @param v
* @return
*/
private int getAdjUnvisiteNode(int v) {
for (int i = 0; i < nNode; i++) {
//代表两个顶点之间是联通的,并且这个顶点没有被访问过
if(adjMal[v][i] == 1 && !nodeList[i].wasVisited) {
return i;
}
}
return -1;
}
}
public static void main(String[] args) {
Graph graph = new Graph();
graph.addNode('A');
graph.addNode('B');
graph.addNode('C');
graph.addNode('D');
graph.addNode('E');
graph.addEdge(0,1);
graph.addEdge(0,3);
graph.addEdge(1,2);
graph.addEdge(1,3);
graph.addEdge(1,4);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(3,4);
graph.mxt();
}
/**
* 求无权图的最小生成树
* @param nums 表示各节点之间是否有连线
* 1表示有 -1表示没有或者其他的表示方法
* 只需要在getToIndex里面改就是了
* @param startIndex 指定起始节点
* @return
*/
public static void getMinTree(int[][] nums,int startIndex) {
//记录那些节点被遍历过了
boolean[] sign = new boolean[nums.length];
//储存临时起始节点的
Stack stack = new Stack<>();
stack.push(startIndex);
sign[startIndex] = true;
while (!stack.empty()) {
int fromIndex = stack.peek(); //当前起点
int toIndex = getToIndex(nums,sign,fromIndex); //下一个点
if(toIndex == -1) {
stack.pop(); //没找到的话直接出栈
}else {
System.out.print(fromIndex+"-->"+toIndex+"\t"); //打印
sign[toIndex] = true; //标记
stack.push(toIndex); //这个节点就是下一次的新起点
}
}
}
/**
* 找一个与当前起点相邻的未被访问的、能到达的节点
* @param nums
* @param sign
* @param fromIndex
* @return
*/
private static int getToIndex(int[][] nums, boolean[] sign, int fromIndex) {
for (int i = 0; i < nums.length; i++) {
if(i == fromIndex) {
continue; //跳过自己
}
//没有被访问、并且和起点之间有连线的
if(!sign[i] && nums[i][fromIndex] == 1) {
return i;
}
}
return -1; //没有了
}
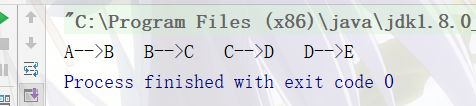
测试代码和运行结果:
public static void main(String[] args) {
int[][] nums = {{0,1,0,1,0},
{1,0,1,1,1},
{0,1,0,1,1},
{1,1,1,0,1},
{0,1,1,1,0},};
getMinTree(nums,0);
}
2、带权图的最小生成树
带权图的最小生成树麻烦点,它的最小生成树算法过程:从一个顶点X(源点)出发找到其他顶点的所有边,放入优先队列,找到权值最小的,把它和所到达的顶点(终点Y)放入树的集合中,再以终点Y作为源点找到所有到其他顶点的边(不包括已放入树中的顶点),放到优先队列中,再从中取最小的把它和它所到达的顶点(终点)放入树的集合中,反复这样操作到全部顶点都放入树中为止;
1、无向带权图的最小生成树

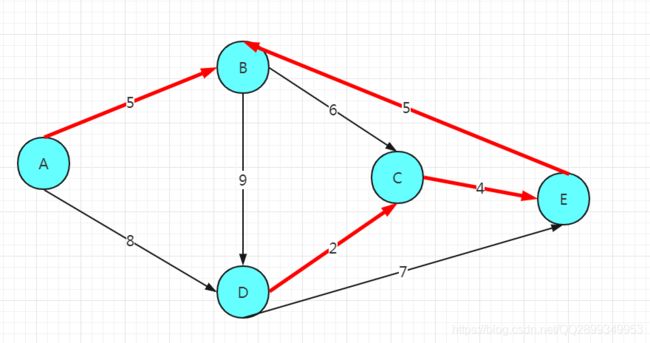
它的最小生成树:

例如上诉图例以A为起点找最小生成树的过程就是:
声明:不能把在优先队列里面已经存在的边、或已经走过的边加到优先队列里面去;
- 以A为起点,将A标记,将A能到达的边(AB、AD)装入优先队列,找最小的边即AB,删除优先队列里面AB这条边;此时A被标记,优先队列里面(AD);
- 以B为起点,将B标记,将B能到达的边装入优先队列,此时优先队列里面的边有(AD、BD、BC、BE),找到最小的边BE,删除优先队列里面的BE这条边;此时A、B被标记,优先队列里面剩下(AD、BD、BC);
- 以E为起点,将E标记,将E能到达的边装入优先队列,此时优先队列里面的边有(AD、BD、BC、EC、ED),找到最小的边CE,删除优先队列里面的CE这条边;此时A、B、E被标记,优先队列里面剩下(AD、BD、BC、ED);
- 以C为起点,将C标记,将C能到达的边装入优先队列,此时优先队列里面的边有(AD、BD、BC、ED、CD),找到最小的边CD,删除优先队列里面的CD这条边;此时A、B、E、C被标记,优先队列里面剩下(AD、BD、BC、ED);
- 以D为起点,将D标记,此时A、B、E、C、D全部被标记,最小生成树查找完成;
下面是代吗实现(把上面的代码中getToIndex方法改一下,有权图需要在所有已经放到优先队列里面的边里面选最短的):
/**
* 求有权图的最小生成树
* @param nums 表示各节点之间是否有连线
* -1表示不能到达、0表示到自己
*
* @param startIndex 指定起始节点
* @return
*/
public static void getMinTree(int[][] nums,int startIndex) {
boolean[] sign = new boolean[nums.length];
//储存临时起始节点的
Stack stack = new Stack<>();
//栈里面装的是前几次选的起始节点,后面找最近距离的时候需要翻翻前面的
stack.push(startIndex);
sign[startIndex] = true;
while (!stack.empty()) {
int[] index = getToIndex(nums,sign,(Stack) stack.clone());
int formIndex = index[0];
int toIndex = index[1];
if(toIndex == -1) {
stack.pop();
}else {
sign[toIndex] = true;
System.out.print(formIndex+"-->"+toIndex+"\t");
stack.push(toIndex);
}
}
}
/**
* 相当于从优先队列里面找最短的那个,并返回最短距离对应的起始、终止节点
* @param nums
* @param sign
* @param stack
* @return
*/
private static int[] getToIndex(int[][] nums, boolean[] sign,Stack stack) {
int formIndex = stack.peek(); //记录起点
int maxVlaue = Integer.MAX_VALUE;
int index = -1; //记录对应的终点
//在前面所有选过的节点对应的边里面挑最短的
while (!stack.empty()) {
int tempStart = stack.pop(); //取出一个作为临时起点
for (int i = 0; i < nums.length; i++) {
if(tempStart == i) {
continue; //跳过自己
}
//没有被访问、并且和起点之间有连线的、且连线是最短的
if(!sign[i] && nums[tempStart][i] != -1 && nums[tempStart][i] < maxVlaue) {
formIndex = tempStart;
maxVlaue = nums[tempStart][i];
index = i;
}
}
}
return new int[] {formIndex,index}; //返回结果
}
上述图例的运行结果:
测试代码:
public static void main(String[] args) {
int[][] nums = {{0,5,-1,8,-1},
{5,0,6,9,5},
{-1,6,0,2,4},
{8,9,2,0,7},
{-1,5,4,7,0},};
getMinTree(nums,0);
}
2、有向带权图的最小生成树

假设还是以A为起点,那么它的最小生成树是:
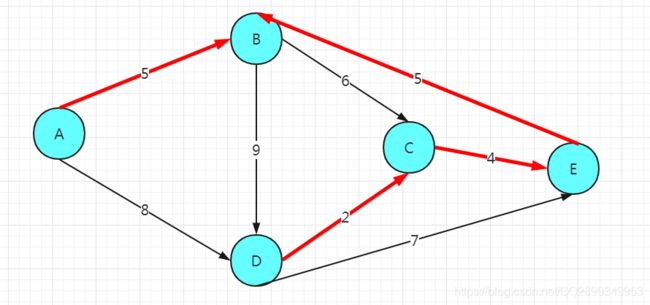
这个和无向带权图的方法差不多,需要改变的就是数组的输入,还有就是两点之间有一个方向上能通就可以,注意我注释注意的地方:
以下就是更改后的有向带权图的最小生成树的代码:
/**
* 求有权图的最小生成树
* @param nums 表示各节点之间是否有连线
* -1表示不能到达、0表示到自己
*
* @param startIndex 指定起始节点
* @return
*/
public static void getMinTree(int[][] nums,int startIndex) {
boolean[] sign = new boolean[nums.length];
//储存临时起始节点的
Stack stack = new Stack<>();
//栈里面装的是前几次选的起始节点,后面找最近距离的时候需要翻翻前面的
stack.push(startIndex);
sign[startIndex] = true;
while (!stack.empty()) {
int[] index = getToIndex(nums,sign,(Stack) stack.clone());
int formIndex = index[0];
int toIndex = index[1];
if(toIndex == -1) {
stack.pop();
}else {
// ============注意====================
if(sign[formIndex]) {
sign[toIndex] = true;
stack.push(toIndex);
}else {
sign[formIndex] = true;
stack.push(formIndex);
}
System.out.print(formIndex+"-->"+toIndex+"\t");
}
}
}
/**
* 相当于从优先队列里面找最短的那个,并返回最短距离对应的起始、终止节点
* @param nums
* @param sign
* @param stack
* @return
*/
private static int[] getToIndex(int[][] nums, boolean[] sign,Stack stack) {
int formIndex = stack.peek(); //记录起点
int maxVlaue = Integer.MAX_VALUE;
int index = -1; //记录对应的终点
//在前面所有选过的节点对应的边里面挑最短的
while (!stack.empty()) {
int tempStart = stack.pop(); //取出一个作为临时起点
for (int i = 0; i < nums.length; i++) {
if(tempStart == i) {
continue; //跳过自己
}
// ==================注意=======================
//没有被访问、并且和起点之间有连线的(两个方向能通就可以)、且连线是最短的
if(!sign[i]) {
if(nums[tempStart][i] != -1 && nums[tempStart][i] < maxVlaue) {
formIndex = tempStart;
maxVlaue = nums[tempStart][i];
index = i;
}
if(nums[i][tempStart] != -1 && nums[i][tempStart] < maxVlaue) {
formIndex = i;
maxVlaue = nums[i][tempStart];
index = tempStart;
}
}
}
}
return new int[] {formIndex,index}; //返回结果
}
然后更改一下数组的输入,我们写测试代码吧:
public static void main(String[] args) {
int[][] nums = {{0,5,-1,8,-1},
{-1,0,6,9,-1},
{-1,-1,0,-1,4},
{-1,-1,2,0,7},
{-1,5,-1,-1,0},};
getMinTree(nums,0);
}
二、克鲁斯卡尔
求最小生成树有两种算法,一种是普利姆算法,我用的就是,还有一种是克鲁斯卡尔算法,有兴趣的可以自己写一下,这是资料链接 → 最小生成树之java实现
最小生成树的起点不一样的话,一般不会影响最小生成树的结果,(如果所有边的权值都不相等的话,以任何不同的节点为起始节点,他们的最小生成树肯定是一样的,如果有那么几条边的权值相等,这就可能会造成最小生成树路径不同,但路径和肯定是一样的);
接着再来试一下有向有权图的:
public static void main(String[] args) {
int[][] nums = {{0,5,-1,8,-1},
{5,0,6,9,5},
{-1,6,0,2,4},
{8,9,2,0,7},
{-1,5,4,7,0},};
for (int i = 0; i < nums.length; i++) {
getMinTree(nums,i);
System.out.println();
}
}

可以看到,除过方向和位置的改变(因为无向图本就不涉及方向),选择的边几乎没变,我们再来试试有向图的吧:
测试代码:
public static void main(String[] args) {
int[][] nums = {{0,5,-1,8,-1},
{-1,0,6,9,-1},
{-1,-1,0,-1,4},
{-1,-1,2,0,7},
{-1,5,-1,-1,0},};
for (int i = 0; i < nums.length; i++) {
getMinTree(nums,i);
System.out.println();
}
}
运行结果:

可以看到,基本变得也就是顺序,下面采用克鲁斯卡尔算法,结果都是一样的,因为它会自己从最短的那条边开始找最小生成树:
算法思想:
- 将图中全部顶点放入生成树中
- 选择联结不同连通分量边权最小的边,将边添加至生成树当中
- 继续执行步骤2,直至生成树上含有n-1条边为止
注:如果图中两个顶点之间存在拓展的边则称这两个顶点为同一连通分量。
代码:
public static void getMinTree(int[][] nums) {
nums = nums.clone();
int i = 1;
while (i < nums.length) { //找n-1次就找完了
int[] path = getToIndex(nums);
int fromIndex = path[0]; //起点
int toIndex = path[1]; //终点
nums[fromIndex][toIndex] = -2; //表示走过了
i++;
System.out.print(fromIndex+"-->"+toIndex+"\t");
}
}
private static int[] getToIndex(int[][] nums) {
int maxVlaue = Integer.MAX_VALUE; //最小距离
int fromIndex = -1; //起点
int toIndex = -1; //终点
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < nums[i].length; j++) {
//如果是自己到自己、或者两点之间无法到达、或者走过了直接跳过
if(i == j || nums[i][j] <= -1) {
continue;
}
if(nums[i][j] < maxVlaue) {
maxVlaue = nums[i][j];
fromIndex = i;
toIndex = j;
}
}
}
return new int[] {fromIndex,toIndex};
}
public static void main(String[] args) {
int[][] nums = {{0, 5, -1, 8, -1},
{-1, 0, 6, 9, -1},
{-1, -1, 0, -1, 4},
{-1, -1, 2, 0, 7},
{-1, 5, -1, -1, 0},};
getMinTree(nums);
}