数据科学家应知必会的6种常见概率分布

CSDN：http://blog.csdn.net/kicilove/article/

前言

假设你是个大学老师。 在检查了一周的作业后，对学生进行了打分。 让录分员创建一个包含所有学生成绩的电子表格，要求是只含分数不含学生姓名等信息。

于是乎，录分员一个大粗心，漏录了好几个分数，介个时候不知道把谁给漏录了。来看看怎么解决这个问题吧。

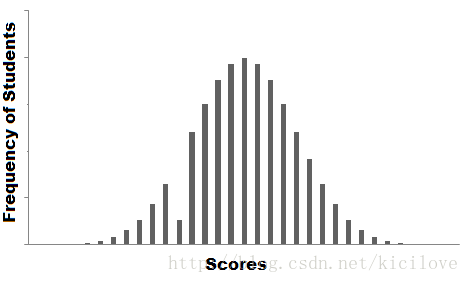
一种方法是可视化已录数据，并从中发现某些数据中的趋势。

上面这个图就是画出来的数据的频率分布图。 可以从图的边缘隐约看到一条光滑的曲线可以用来定义我们的数据，但是我们也得注意到一个异常，有个段的柱条缺半截似的，也就是这一段分数范围内的频率异常低。所以最好是能有些值来把这个短半截给补上。

这就是一个现实生活中用数据分析解决问题的一个例子。对任何科学家而言，不管你是个学生或者是专家，分布是一个必知的概念。因为这是分析和统计推断的基础。

概率概念给了我们计算它的方法，分布才是帮我们看清数据背后的暗泉涌动。

目录：

1. 常见数据类型
2. 分布类型
   
   1. 伯努利分布（Bernoulli Distribution）
   2. 均匀分布（Uniform Distribution）
   3. 二项分布（Binomial Distribution）
   4. 正态分布（Normal Distribution）
   5. 泊松分布（Poisson Distribution）
   6. 指数分布（Exponential Distribution）
3. 分布之间的关系
4. 测一测

一、常见数据类型

在正式的解释分布之前，我们先来看一看平时遇到的数据。数据可大致分为离散型数据和连续型数据。

离散型数据

离散型数据顾名思义就是只取几个特定的值。例如：当你掷骰子的时候，结果只有1,2,3,4,5,6，不会出现类似1.5,2.5。

连续型数据

在一个给定的范围内，连续型数据可以取任意值。这个范围可以是有限的或者是无穷的。例如：一个人的体重或者身高，可以取值54kg,54.4kg,54.33333kg等等都没有问题。

下面就开始介绍分布的类型。

二、分布类型

伯努利分布（Bernoulli Distribution）

首先从最简单的分布开始，伯努利分布实际上是一个听起来最容易理解的分布。

伯努利分布一次实验有两个可能的结果，比如1代表success及0代表failure。随机变量 X 一个取值为1并代表成功，成功概率为 p ，一个取值为0表示失败，失败概率为 q 或者说 1−p 。

这里，概率分布函数为 px(1−p)1−x ，其中 x∈(0,1) ，我们也可以写成如下形式：

P(x)={1−p，p，x=0x=1

成功和失败的概率没必要相同，也就是没必要都是0.5，但是这俩概率加和应该为1，比如可以是下面的图：

这个图就是 p(success)=0.15，p(failure)=0.85 。

下面说一下随机变量的期望，一个分布的期望就是这个分布的均值。服从伯努利分布的随机变量 X 的期望值就是：

E(X)=1∗p+0∗(1−p)=p

服从伯努利分布的随机变量的方差是：

V(X)=E(X2)−[E(X)]2=p−p2=p(1−p)

还有许多伯努利分布的例子，比如说明天是否会下雨，今天会不会去健身，明天乒乓球比赛是不是会赢。

均匀分布（Uniform Distribution）

当你掷骰子的时候，结果出现1到6中的任何一个，而任何一个结果出现的概率都是相同的，这就是均匀分布最原始的雏形。你可能看出来了，与伯努利分布不同的是，这 n 个出现的结果的概率都是相同的。

一个随机变量 X 为均匀分布是指密度函数如下：

f(x)=1b−a−∞<a≤b<∞

下图为均匀分布的密度图的样子：

咱们可以看出来均匀分布的密度图是个矩形，这也就是为啥均匀分布的昵称是矩形分布。

对于均匀分布来说 a 和 b 都是参数，分布的参数。

例子：假如花店每日销售的花束数量均匀分布，最多40只，最少10只。

我们来尝试计算每日卖花数量在15到30之间的概率。由于随机变量所有可能发生的事件的概率和为1，并且卖花数量是均匀分布，所有在15到30之间的概率为 (30−15)∗1(40−10)=0.5 。类似的对于每日卖花数量大于20发生的概率就是 1−(20−10)∗1(40−10)=23 。

若随机变量 X 服从均匀分布，那么它的均值和方差分别为：

Mean-> E(X)=(a+b)2

Variance-> V(X)=(b−a)212

标准的均匀分布的密度参数为 a=0 和 b=0 ，所以对于标准的均匀分布的密度函数为：

f(x)={1，0，0≤x≤1otherwise

二项分布（Binomial Distribution）

我们假定一个随机变量，比如 X ，表示你赢得比赛的次数。 X 可能的值是什么？ 它可以是任何数字，赢得比赛的次数。

如果就两个可能的结果。 成功，失败。 因此，成功概率= 0.5，失败的概率可以容易地计算为： q=p−1=0.5 。

只有两种结果是可能的分布，如成功或失败，以及所有试验的成功和失败概率相同的情况称为二项分布。

发生结果的可能性不同时， 前面的例子如果实验成功的概率是0.2，那么失败的概率可以很容易地计算出来， q=1−0.2=0.8 。

每次试验都是独立的，因为之前的结果并不决定或影响当前的结果。 只有两次重复n次的可能结果的实验称为二项式。 二项分布的参数是 n 和 p ，其中 n 是试验的总数， p 是每个试验中成功的概率。

基于上述解释，二项分布的性质是：

1. 每次实验独立
2. 试验中只有两种可能的结果 - 成功或失败。
3. 共进行了 n 次相同的试验。
4. 所有试验的成功和失败的概率是相同的。 （试验是相同的。）

二项分布的数学表达式由下式给出：

P(x)=n!(n−x)!x!pxqn−x

一个二项分布图，其中成功的概率不等于失败的概率长这样：

成功概率与失败概率相等，长这样：

二项分布均值和方差：

Mean -> μ=n∗p

Variance -> Var(X)=n∗p∗q

正态分布（Normal Distribution）

正态分布可以表示宇宙中大多数的事件发生情况。 如果任何分布具有以下特征，则称为正态分布：

1. 均值、中位数、众数在一个分布中取相同的值；
2. 分布曲线关于 x=μ 对称；
3. 曲线下面的面积总和为；
4. 中心位置的左半边和右半边对应位置的概率取值相同。

正态分布与二项分布有很大的不同。 但是，如果试验次数接近无穷大，则形状将非常相似。

服从正态分布的随机变量 X 的密度函数为：

f(x)=12πσ−−−√e{−12(x−μσ)2}−∞<x<∞

服从均匀分布的随机变量 X 的均值和方差，如下：

Mean -> E(X)=μ
Variance -> Var(X)=σ2

这里 μ (mean)和 σ (standard deviation)是两个参数，随机变量 X∼N(μ,σ) 的不同取值的变化图如下：

标准正态分布的均值为0，方差为1，密度图如下：

f(x)=12π−−√e−x22∞<x<∞

泊松分布（Poisson Distribution）

假设你在一个呼叫中心工作，大概一天能接收到多少个电话？ 它可以是任何数字。 呼叫数量就可以用泊松分布建模，下面是别的例子：
1. 每天在医院记录的紧急呼叫数量。
2. 每天在一个地区报告的盗窃数量。
3. 一小时内到达沙龙的客户数量。
4. 一个特定城市报告的自杀人数。
5. 书每页的打印错误数量。

泊松分布适用于事件发生在任意随机时间点或者空间的情况，其中我们的兴趣仅在于事件的发生次数。 当以下假设有效时，分布称为泊松分布：

• 任何成功的事件都不应该影响另一个成功事件的结果。
• 在较短的时间间隔内成功的概率必须等于在较长的时间间隔内成功的概率。
• 随着间隔变小，间隔内成功的概率接近零。 现在，如果任何分布满足上述假设，那么它是一个泊松分布。

泊松分布中使用的一些符号是：

• λ 是事件发生的速率
• t 是时间间隔的长度
• X 是在时间间隔 t 内事件发生的次数

这里 X 叫做泊松随机变量，同时 X 的概率分布就叫做泊松分布。

我们用 μ 表示时间 t 内时间发生的平均次数也就是均值，所以 μ=λ∗t 。

服从泊松分布的随机变量 X 的PMF为：

P(X=x)=e−uμxx!x=0,1,2,......

均值 μ 是分布的参数， μ 也被定义为在一个时间段内发生 λ 次。泊松分布图如下：

下图显示了均值增加而导致的曲线移动：

可以感觉到，随着平均值的增加，曲线向右移动。
服从泊松分布的随机变量 X 的均值和方差：

Mean -> E(X)=μ

Variance -> Var(X)=μ

指数分布（Exponential Distribution）

我们再来考虑一下呼叫中心的例子。 想想通话间的时间间隔是多少？ 指数分布来解决我们的问题。 指数分布对呼叫之间的时间间隔建模。

其他例子：
1. 两站地铁到达之间的时间长度
2. 到达加油站的时间长度
3. 空调的使用寿命

指数分布广泛用于生存分析。 从机器的预期寿命到人的预期寿命，指数分布可用来传递这些结果。

随机变量 X 服从指数分布，它的PDF 为：

f(x)=λeλx,x≥0

参数 λ>0 也叫做速率。

对于生存分析， λ 被称为设备在任何时间 t 的故障率，假设它存活到t。

服从指数分布的随机变量 X 的均值和方差：

Mean -> E(X)=1λ

Variance -> Var(X)=(1λ)2

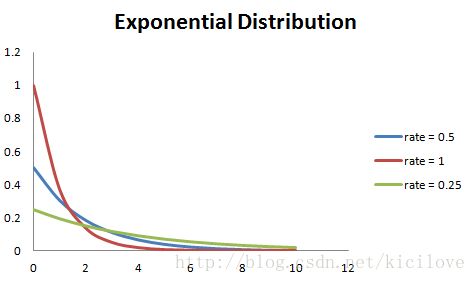
此外，速率越大，曲线越下降快，速率越低，曲线越平滑。 下图显示了这一点：

为了简化计算，下面给出了一些公式。 P{X≤x}=1−e−λx 对应于 x 左边密度曲线下的面积。

P{X>x}=1−e−λx 对应于 x 右侧密度曲线下的面积。

P{x1<X≤x2}=e−λx1−e−λx2 对应于 x1 和 x2 之间密度曲线下的面积。

三、分布之间的关系

伯努利分布和二项分布

1. 伯努利分布是二项分布的一个特例，只有一次试验。

2. 伯努利和二项分布只有两种可能的结果，即成功和失败。

泊松分布和二项分布

泊松分布是二项分布的极限分布，条件如下：
1. 试验次数足够多或者说 n -> ∞
2. 每次试验成功的概率相同，无穷小或者 p ->0
3. np=λ ，有限。

正态分布和二项分布 & 正态分布和泊松分布

正态分布是在以下条件下二项分布的另一种极限形式，条件如下：
1. 试验次数无限大 n -> ∞
2. p 和 q 都不是无限小的。

正态分布也是参数 λ -> ∞ 的泊松分布的一个极限情况。

指数分布和泊松分布

如果随机事件之间的时间遵循速率为 λ 的指数分布，那么长度为 t 的时间段内的事件总数遵循具有参数 λt 的泊松分布。

总结

概率分布在许多领域都很普遍，即保险学，物理学，工程学，计算机科学甚至社会科学，其中心理学和医学学生广泛使用概率分布。 它有一个简单的应用程序和广泛的使用。 这篇文章强调了在日常生活中观察到的六个重要分布，并解释了它们的应用。 现在你将能够识别，关联和区分这些分布。

CSDN：http://blog.csdn.net/kicilove/article/