神经网络剖析激活函数优缺点（Undetanding the difficulty of training deep feedforward neural networks）

摘要：在2006年以前，似乎深度多层的神经网络没有被成功训练过。自那以后少数几种算法显示成功地训练了它们，实验结果表明了深度多层的架构的优越性。所有这些实验结果都是通过新的初始化或训练机制获得的。我们的目标是更好地理解为什么随机初始化的标准梯度下降法在深度神经网络下表现如此糟糕，为了更好地理解最近的相对成功并帮助设计未来更好的算法。我们首先观察了非线性激活函数的影响。我们发现logistic sigmoid激活不适用于随机初始化的深度网络，因为它的平均值，特别是顶部隐藏层进入饱和状态。令人惊讶的是，我们发现饱和单位可以移出自我饱和，尽管低，并且在训练神经网络时解释有时会出现高原。我们发现饱和度较低的新非线性通常是有益的。最后，我们研究层和训练过程中激活和梯度如何变化，当训练可能更加困难时，与每层相关联的雅可比矩阵的奇异值远不等于1。基于这些考虑，我们提出了一种新的初始化方案，其带来显着更快的收敛。

介绍这篇论文的主要内容就是尝试更好的理解为什么使用“标准随机初始化”来计算使用标准梯度下降的网络效果通常来讲都不是很好。

首先研究了不同的非线性激活函数的影响，发现 sigmoid 函数它的均值会导致在隐层中很容易到达函数的饱和区域，因此sigmoid
激活函数在随机初始化的深度网络中并不合适。但同时惊喜的发现，处于饱和的神经元能够自己“逃脱出”饱和状态。

最后研究了激活值和梯度值如何在训练过程中的各层次里发生变化，其中，当与每个层相关联的雅可比矩阵的奇异值远远大于1时，训练可能会变得更加困难。基于这些考虑，提出了一种新的初始化方法，可以带来更快的收敛速度。

为什么使用非线性的激活函数？而不是线性的函数：
因为非线性的激活函数可以拟合非线性的曲面，而不是一条直线，分离边界更加灵活。

这边论文模型采用了多个激活函数：
使用softsign是因为他不会过快的接近饱和，三次多项的非线性，而不是指数级别的非线性
饱和的速度会慢一点。

饱和的时候，梯度接近于0，什么都学习不到了。
接近于两边也不好，接近于0出也不好，太过于线性了
softsign非线性的部分范围更大

每一层的均值和标准差：
可以看到后面的曲线很快就达到饱和了
所以bp神经网络如果你的层数非常多，就很容易达到饱和值

1 深度神经网络

深度学习方法的目标是通过低层次特征的组合形成更高层次的特征层次结构。它们包括用于各种深层架构的学习方法，包括具有许多隐藏层的神经网络（Vincentet al。，2008）和具有多层隐变量的图形模型（Hinton等，2006）等（Zhuet al。， 2009; Weston等，2008）。由于它们的理论吸引力，来自生物学和人类认知的灵感以及由于视觉的经验成功（Ranzato等人，2007; Larochelle等人，2007），因此他们最近注意到了它们（参见（Bengio，2009） 2007; Vincent等，2008）和自然语言处理（NLP）（Collobert＆Weston，2008; Mnih＆Hinton，2009） 的联系。Bengio（2009）回顾和讨论的理论结果表明，为了学习能够代表高级抽象的复杂功能（例如，在视觉，语言和其他AI级任务中），可能需要深层架构。最近的深层结构实验结果是通过模型得到的，这些模型可以转化为中间监督神经网络，但初始化方法不同于经典的前向神经网络（Rumelhart et al。，1986）。为什么这些新算法比标准随机初始化和基于梯度的无监督训练准则优化工作得更好？部分答案可能在最近对无监督预训练效果的分析中发现（Erhan等人，2009），表明它起着规范化的作用，在优化过程的“更好”盆地中初始化参数，对应于明显的局部但与早期的工作（Bengio等人，2007）相比，即使是纯粹的监督但贪婪的分层过程也会带来更好的结果。因此，在这里，我们不是专注于无监督的预培训或半监督标准给深层架构带来什么，而是专注于分析好的旧（但深度）多层神经网络可能出现的问题。我们的分析是由调查实验驱动到monitrogen激活（注意饱和我们还评估了这些激活函数选择（以及它可能影响饱和度的思想）和初始化过程（由于无监督预训练是一种特殊形式的初始化，并且它具有隐含单位） adrastic影响）。

2 实验设置和数据集

生成本节介绍的新数据集的代码可从以下网址获得

http://www.iro.umontreal.ca/˜lisa/twiki/bin/view.cgi/Public/DeepGradientsAISTATS2010

2.1无限数据集的在线学习：

Shapeset-3 × 2：总共3种类型的图（椭圆，方框，三角），每张图片从里面随机选两个

我们将这个数据集称为Shapeset-3×2数据集，图1中的示例图像（顶部）。 Shapeset-3×2包含1或2个二维物体的图像，每个物体取自3个形状类别（三角形，平行四边形，椭圆形），并放置有随机形状参数（相对长度和/或角度），缩放，旋转，平移和灰度。

我们注意到，图像中只有一个形状，识别它的任务太简单了。因此，我们决定对两个物体的图像进行取样，限制第二个物体与第一个物体不超过其面积的百分之五十，以避免完全隐藏它。（不大于50%的覆盖）

任务是预测存在的物体（例如三角形+椭圆，平行四边形+平行四边形，单独三角形等），而不必区分前景形状和背景形状。这因此定义了九个配置类。

该任务相当困难，因为我们需要发现旋转，平移，缩放，对象颜色，遮挡和形状的相对位置等方面的不变性。同时，我们需要提取预测哪些物体形状存在的可变性因素。

图像的大小是任意的，但我们将其固定为32×32，以便有效地处理高密度网络。

2.2 有限数据集

MNIST数字（LeCun等人，1998a）数据集有50,000个训练图像，10,000个验证图像（用于超参数选择）和10,000个测试图像，每个图像显示10个像素之一的28×28灰度像素图像数字。 CIFAR-10（Krizhevsky＆Hinton，2009）是微型图像数据集的标记子集，其中包含50,000个训练样例（我们从中提取10,000个作为验证数据）和10,000个测试样例。每个图像中对应于主要对象的有10个类别：飞机，汽车，鸟，猫，鹿，狗，青蛙，马，船或卡车。这些课程是平衡的。每个图像都是彩色的，但尺寸仅为32×32像素，因此输入是32×32×3 = 3072个实际值的向量。 Small-ImageNet，它是一套微小的37×37灰度级图像数据集，由http://www.image-net.org上的高分辨率和更大集合计算得出，带有来自WordNet名词层次结构的标签。我们已经使用了90,000个示例进行培训，10,000个用于验证组，10,000个用于测试。有10个平衡类：爬行动物，车辆，鸟类，哺乳动物，鱼类，家具，仪器，工具，鲜花和水果图1（底部）显示随机选择的例子。

2.3实验设置

使用的是一个具有 1-5 层深度的，每层具有1000个神经元节点，输出层使用一个 softmax logistic regression，代价函数是 −logP(y|x) 。

我们优化了具有一至五层隐藏层的前馈神经网络，每层有一千个隐藏单元，并对输出层进行了softmax逻辑回归。代价函数是负对数似然-log P（y | x），其中（x，y）是（输入图像，目标类）对。神经网络在10个小批量的随机反向传播上进行了优化，即@ -log P（y | x）训练对（x，y）的平均g并用于更新参数？在那个方向，与？ ？ - ？g。学习率？是在大量更新（500万）后基于验证集错误进行优化的超参数。我们改变了隐藏层中非线性激活函数的类型：sigmoid 1 /（1 + e-x），双曲正切tanh（x）和一个新提出的激活函数（Bergstra等人，2009年） softsign，x /（1 + | x |）。软标志类似于双曲正切（它的范围是-1到1），但它的尾部是二次多项式而不是指数，即它接近它的渐近线要慢得多。在比较中，我们分别为每个模型搜索最佳超参数（学习速率和深度）。请注意，Shapeset-3×2的最佳深度总是5，除了S形，它是四个。我们使用以下常用启发式将偏差初始化为0和各层的权重Wij：

3 激活功能的影响与训练期间的饱和度

3.1 Sigmoid实验

在选择激活函数时，我们总要避免两点：
1、避免激活函数处于过饱和状态，在这种状态，梯度就不能很好的得到传递。
2、激活函数过度线性化，因为只有非线性才能拟合更多的函数。

避免激活函数处于过饱和状态，在这种状态，梯度就不能很好的得到传递。
激活函数过度线性化，因为只有非线性才能拟合更多的函数。

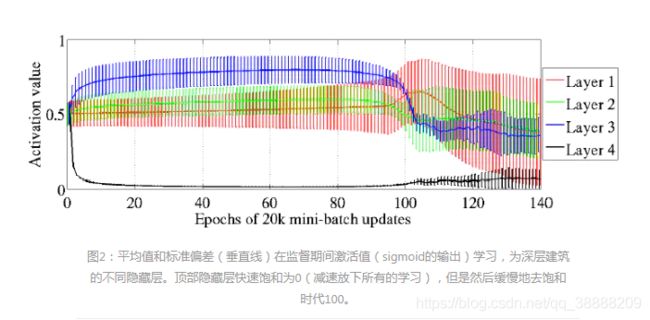
Sigmoid非线性已经被证明可以减慢学习，因为它的非零均值在Hessian中引入了重要的奇异值（LeCun et al。，1998b）。在本节中，我们将看到由于深度前馈网络中的激活功能导致的另一个症状行为。我们希望通过查看训练过程中激活的演变来研究可能的饱和度，本节中的数字显示了Shapeset-3×2数据的结果，但在其他数据集中观察到类似的行为。图2显示了在用S形激活函数训练深层结构期间，每个隐藏层激活值（在非线性之后）的演变。第1层是指第一个隐藏层的输出，并且有四个隐藏层。该图显示了这些激活的平均值和标准偏差。这些统计数据和直方图是在学习期间的不同时间计算的，通过查看300个固定测试示例的激活值。

图说明：竖直方向表示激活值，其中实线表示的是均值，上下的浮动表示上下标准差，水平方向表示迭代的次数

第四层的输出会过于饱和，可以看到在100次迭代之后，所有的输出都接近饱和了

我们看到在开始时非常快速地，最后一个隐藏层的所有S形激活值被推到其较低的饱和度值0.相反，其他层的平均激活值大于0.5，并且随着我们从 输出层到输入层, 我们发现这种饱和在具有S形激活的更深网络中可以持续很长时间. 例如，在训练期间，深度模型从未逃脱这种制度。 令人惊讶的是，对于中间数量的隐藏层（这里是四层），饱和状态可能会逃脱。 在顶层隐藏层移出饱和的同时，第一个隐藏层开始饱和并因此趋于稳定。

我们可以看到，对于第 1~4 层，其均值都在 0.5 左右，且按照输出到输入方向激活值依次降低，但这个位置处于 Sigmoid 函数的线性区附近，而第 5 层在迭代的过程中很快就到达了饱和区，而且这种饱和状态会持续很长的时间，很可能在整个训练过程中这一层都处于饱和状态。但是，令人惊奇的是，随着迭代次数的增加，第 5 层隐层有 “逃离” 饱和状态的趋势，而前面的 4 层有逐渐趋于饱和的趋势，因此会逐渐趋于稳定。

我们假设这种行为是由于随机初始化和隐藏单元输出为0对应于饱和S形的事实相结合。注意，具有S形但是从无监督预训练（例如从RBM受限的玻尔兹曼机）初始化的深网络不会受到这种饱和行为的影响。我们提出的解释依赖于这样一个假设：随机初始化网络的低层计算最初对分类任务没有用处，与从无监督预训练获得的变换不同。逻辑层输出softmax（b + Wh）最初可能更多地依赖于它的偏差b（其被快速学习）而不是依赖于从输入图像导出的最高隐藏激活h . 因为h将以不能预测y ，可能主要与x的其他可能更主要的变化相关。因此，误差梯度倾向于将Wh推向0，这可以通过将h推向0来实现。在对称激活函数（如双曲线正切和软标志）的情况下，坐在0附近是好的，因为它允许梯度向后流动。然而，将S形输出推到0会使它们进入饱和状态，这将防止梯度向后流动，并防止较低层学习有用的特征。最终但是慢慢地，较低层向更有用的特征移动，并且顶端隐藏层然后移出饱和区域。但请注意，即使在此之后，网络也会转变为质量较差的解决方案（也就是泛化）那么发现具有对称激活功能的那些， 可以在图11中看到。

对于上面这种情况，文中假设是由于 采用随机初始化和对于饱和的 Sigmoid 函数输出接近为 0 共同造成的。同时也应该注意到，对于经过 pre-training 的深度网络并不会出现这种饱和情况。所以，前面几层的输出对于最后输出的各类的预测是基本没有作用的，或者说直到第三层为止，前几层的输出都是随机的，而非像经过了 pre-training 得到的初始化参数，预训练得到的初始化参数是有意义的。第四层的输出加权后的值直接影响到的最后的代价函数的，因为它后面接的是 softmax 的输出层的，因此，输出层的 softmax(b+Wh) 的最终正确性可能更依赖于偏置 b 而非由前几层共同作用得到的 h，因此为了在一开始让 h 的值不至于影响到 b+Wh 值，网络自己就在代价函数的作用下学习了，学习的结果就是：反向梯度算法导致 Wh 的结果趋向于0，而这可以通过让 h 趋向于 0 来完成，偏置 b 迅速学习，并支撑起了整个预测结果。但是同时，将 h 推向 0 会导致处于 Sigmoid 函数的饱和区，使得反向梯度学习缓慢。最终 (但会经过很长时间 )，前面的隐层会向提取更有意义的特征方向移动，而最后层也会逐渐移出饱和区，但是即便是在这样之后，网络最终也无法得到很好的训练效果 (以及泛化能力)。

3.2 双曲正切的实验
如上所述，双曲正切网络没有遭受顶级隐藏的那种饱和行为因为它的S形网络观察到的层对称度在0.左右。但是，用我们的标准重量

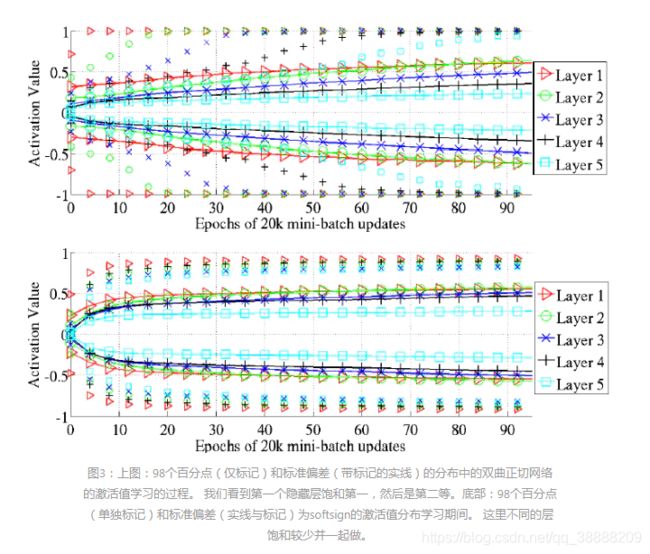
初始化，我们观察到一个连续发生饱和现象从第1层开始在网络中传播，如图3所示。为什么会发生这种情况仍有待了解。

上面提到了 Sigmoid 函数在 0 附近会到达饱和区域，但是 tanh 函数在 0 附近则不会达到饱和，因为 tanh 函数在 0 附近呈现对称线性特征，但是，使用标准权重分布来初始化权重，我们会发现同样会很快达到饱和状态，正如下图中所示，为什么会出现这种情况还需要进一步讨论。

图片说明：上面两张图分别是 tanh 作为激活函数的激活值情况和 softsign 函数作为激活函数的激活值情况。其中实线表示上下标准差，而没有实线的点则表示 98% 的数据分布。首先看上面的图像，可以看出从第一层到第五层，在标准均匀初始化权值的前提下，逐渐每层都慢慢到了饱和区， 对于这个现象，文中也没有给出合理的解释。再观察下面的图像，可以看出 softsign 函数的激活值比 tanh 函数的激活值区域饱和区的速度慢，因此效果也就更好。

3.3 Softsign的实验

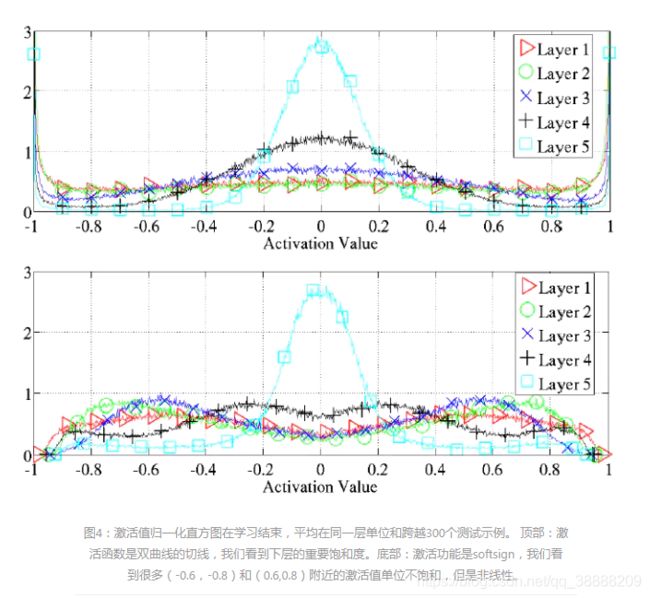
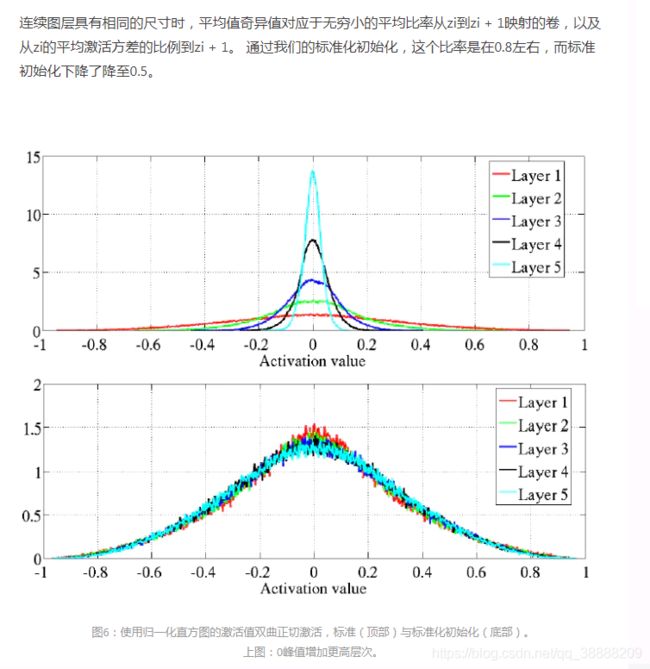
Softsign x /（1 + | x |）类似于双曲正切，但由于它的渐近线（多项式而不是指数），可能在饱和度方面表现不同。 我们在图3上看到饱和不会像双曲线正切那样发生在另一层之后。 它在开始时更快，然后缓慢，并且所有层一起朝着更大的权重移动。 我们还可以在训练结束时看到激活值的直方图与双曲线切线的直方图有很大不同（图4）。 而后者产生激活分布的模式主要在极端（渐近线-1和1）或大约0处，软标志网络在其膝盖周围具有激活模式（在0和-1之间的平坦状态和1）。 这些区域存在非常大的非线性，但梯度将流动良好。

图像说明：上面两图示激活值在学习结束时归一化的直方图，分布在同一层上的所有神经元和300个测试示例。两幅图中上面的表示的是激活函数为 tanh ，下面表示的是激活函数为 softsign，处在 0 附近的激活值是线性区，而 (-0.8, -0.6) 和 (0.6, 0.8) 区域处于非线性区。

Softsign 函数在形状上与 tanh 函数具有一定的相似性，但是在前面也有提到，在趋近渐近线的速度上，tanh 是指数级趋近，而 softsign 则是二次趋近。图 3 给出的是 tanh 激活函数与 softsign 激活函数在训练完成以后的激活值的分布图。

我们可以看到对于 tanh 激活函数，它的激活值大多分布在 -1 和 +1 处，而这两个位置都是出于饱和区的位置，第 5 层还有许多出于 0 附近的激活值，但是对于 tanh 激活函数，0 附近具有良好的线性性质，而不具有良好的非线性性质，因此对于拟合函数来说整体并不理想。

对于 softsign 函数，我们可以看到处于饱和取得值并不占数据的大多数，除了第 5 层有相当数量的激活值处于0附近，其余隐层的激活值在 (-0.8, -0.6) 和 (0.6, 0.8) 这两个非线性区也有大量的分布，因此具有良好的非线性拟合能力，对于拟合函数来说比较理想。

4 梯度及其传播的 研究

4.1成本函数的影响

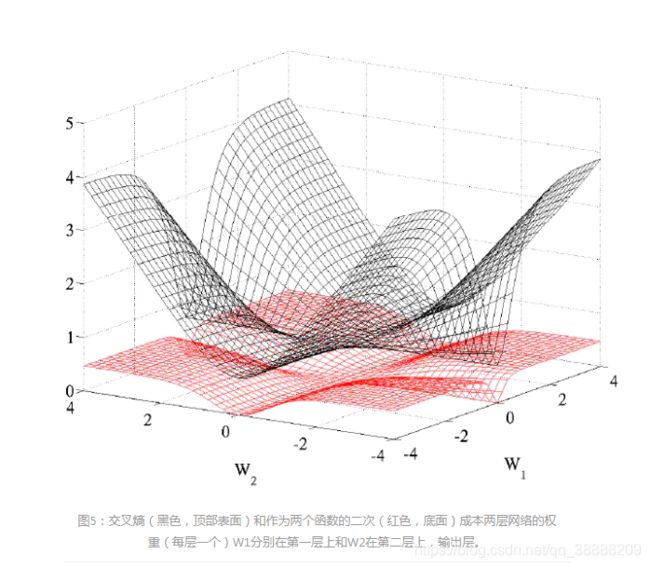
我们发现逻辑回归或条件对数似然成本函数（-log P（y | x）加上softmax输出）比传统上用于训练前馈神经网络的二次成本（分类问题）好得多 Rumelhart等，1986）。 这不是一个新的观察结果（Solla et al。，1988），但我们发现在这里强调这一点很重要。 我们发现训练准则中的平稳（作为参数的函数）较少出现在对数似然成本函数中。 我们可以在图5中看到这一点，该图将训练准则描绘为具有双曲正切单位的双层网络（一个隐藏层）以及随机输入和目标信号的两个权重的函数。 平均成本显然更严重。

4.2初始化时的梯度

4.2.1理论考虑和新的规范化初始化

我们研究反向传播的梯度，或等价的投影偏差在每一层的成本函数的梯度。 布拉德利（Bradley，2009）发现，在初始化之后，随着从输出层向输入层移动，反向传播梯度变小。 他研究了在每一层都具有线性激活的网络，发现随着我们在网络中倒退，反向传播梯度的方差减小。 我们也将从研究线性状态开始。

在1986年 Rumelhart 已经发现：logistic function 或者叫 conditional log-likelihood function: -log P（y|x) 的效果比 quadratic cost function（平方代价函数）的效果好很多的，原因在于 quadratic cost function（平方代价函数）在训练过程中会出现更多的 plateaus（平坦区域）。文章给出了一个两个参数下的图，图中采用的是具有单隐层的神经网络，激活函数使用的是 tanh 函数，对于输入信号进行随机初始化，可以看到二次代价函数具有更多的 plateaus （平坦区域）。

说明：图中上面的曲面表示的是交叉熵代价函数，下面的曲面表示的是二次代价函数，W₁ 和 W₂ 分别表示层与层之间的连接权值。

4.2 Gradient at initialization

说明，这部分是这篇论文的重点内容，提出了一种新的权重初始化方法。

4.2.1 Theoretical Considerations and a New Normalized Initialization

对于使用对称激活的稠密人工神经网络函数f的单位导数为0（即f0（0）= 1），如果我们为第i层的激活矢量写si和si层i的激活函数的参数向量，

这部分基于 Bradley 在 2009 年的理论分析 the variance of the back-progated gradients，并提出一种新的权值初始化的方法。

进行翻译：
我们研究反向传播的梯度，或是代价函数对于每一层输入偏置的梯度。Bradley 在 2009 年发现在初始化权重后反向梯度从输出层到输入层逐渐减小。它使用线性的激活函数，发现了反向传播的梯度的方差随网络的向后而逐渐减小，在这部分的开始，我们在线性领域进行研究。

对于一个密集连接的使用线性激活函数的 ANN，且激活函数在 0 处的导数值为 1，即有 f’(0) = 1，这里我们设 zⁱ 是第 i 层的激活向量，sⁱ 表示输入第 i 层激活函数的向量，所以有 si=ziWi+bisi=ziWi+bi 和 zi+1=f(si)zi+1=f(si)，从这些定义中可以得到下面这两个式子：


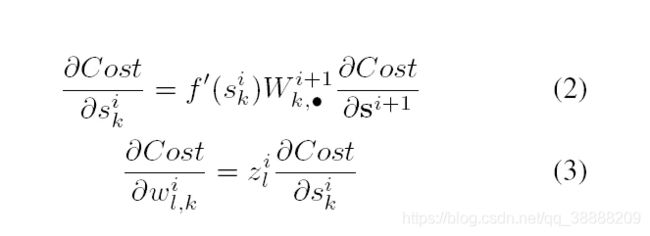
下面这部分是这篇论文的重点，但是觉得这部分的推导部分比较繁琐，查阅资料发现了这两篇博客

http://blog.csdn.net/kangroger/article/details/61414426

http://blog.csdn.net/u011534057/article/details/51673458

这两部分的推导比较容易理解。这里不再赘述。

Ps. 重点是记住这种初始化权值的方法，这在以后的深层网络中也会经常用到。

方差可以用输入，输出和随机权重初始化推导得出，考虑考虑我们在初始化时处于线性状态的假设，权重是独立初始化的，输入特征差异是相同的 ( = Var[x] )，然后我们就可以得出，对于第 i 层共有 n_i 个神经元和网络的输入向量为 x ，有下面的公式：

我们为第i层的所有权重的共享标量方差写入Var[W^i’]，因此，对于一个有 d 层的神经网络：

对于一个前向网络来说，为了保持信息的流动，我们希望有：
而对于一个误差反向传播的网络来说，我们希望有：

从上面这两个条件我们就可以推断出：
由上面这两个公式可以推出下面的式子：

需要说明的是，当着两个条件都同时满足时，需要满足所有层的宽度都是相同的，如果我们使用同样的初始化方法对权重进行初始化，就能够得到下面这两个很有意思的结论：
可以看出，对于每一层上的权重的方差都是相等的，但是随着我们考虑更深入的网络，反向传播梯度的方差可能会消失或爆炸。 注意，在研究递归神经网络时，在时间上可以看出是非常深入的网络。

我们使用的标准初始化（eq.1）产生了以下属性的差异：

这里 n 表示的是每一层网络的神经元个数 (假设所有层具有所有相同的神经元数)，而这就会导致 BP 算法的梯度的方差取决于层数。

因此，由于通过层次间的乘法效应来初始化深层网络，归一化因子可能很重要，我们建议使用以下初始化过程大致满足维护激活方差和反向传播梯度方差的目标，考虑到网络向上或向下移动。


剩下的分析可参考：https://blog.csdn.net/qq_34784753/article/details/78668884

4.3 学习过程中的后向传播梯度

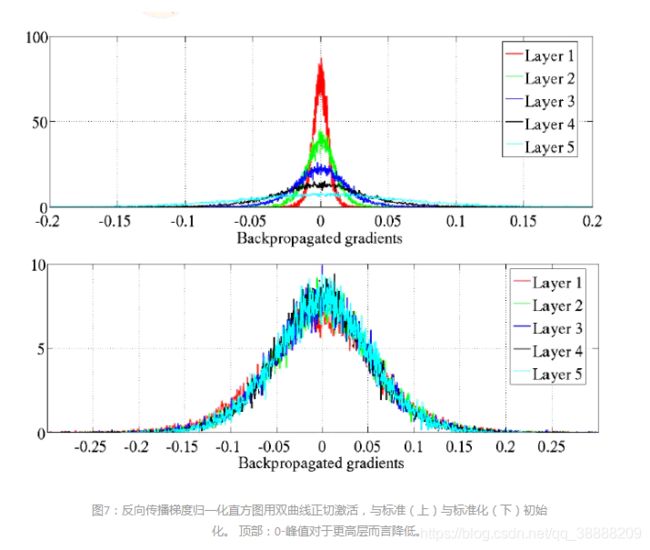
这种网络中的学习动态非常复杂，我们希望开发更好的工具来分析和跟踪它们。 特别是，我们不能在理论分析中使用简单的方差计算，因为权值不再与激活值无关，并且线性假设也被违反。 正如Bradley（2009）首先指出的那样，我们观察到（图7），在训练开始时，在标准初始化（方程1）之后，向后传播的向后传播梯度的方差变小。 然而，我们发现这种趋势在学习期间很快就会逆转。 使用我们的标准化初始化，我们看不到如此递减的反向传播梯度（图7的底部）。

最初令人惊讶的是，即使当后向传播梯度变小（标准初始化）时，如图8所示，各层间权重梯度的方差大致保持不变。然而，这可以通过我们上面的理论分析来解释等式14）。有趣的是，如图9所示，这些关于标准和规范化初始化权重梯度的观察结果在训练期间发生了变化（这里为tanh网络）。事实上，尽管梯度起初大致相同，但随着训练的进行，它们彼此不同（在较低层中梯度较大），特别是在标准初始化时。请注意，这可能是归一化初始化的优点之一，因为在不同层次上具有非常不同幅度的梯度可能会导致病态调节和较慢的训练。最后，我们观察到softsign网络与标准化初始化的tanh网络有相似之处，这可以通过比较两种情况下的激活演变来看出（参见图3-底部和图10）。

5 误差曲线和结论

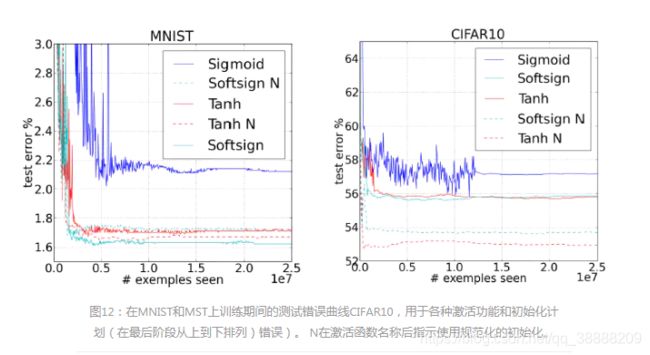
我们关心的最后一点是使用不同策略进行培训的成功，并且最好用错误曲线来说明，这些错误曲线显示随着培训进程和渐近线的发展，测试错误的演变。 图11显示了在Shapeset-3×2上进行在线培训的曲线，而表1给出了所有研究数据集（Shapeset-3×2，MNIST，CIFAR-10和Small-ImageNet）的最终测试误差。 作为基准，我们对10万个Shapeset样例优化了RBF支持向量机模型，并获得了59.47％的测试误差，而在同一组中，我们获得了50.47％的具有标准化初始化的深度为5的双曲正切网络。

这些结果说明了选择激活和初始化的效果。 作为一个参考，我们在图11中包括了在无监督预训练和去噪自动编码器之后从初始化获得的监督微调的误差曲线（Vincent等，2008）。 对于每个网络，分别选择学习率来最小化验证集上的错误。 我们可以指出，在Shapeset-3×2上，由于任务的困难，我们在学习过程中观察到重要的饱和度，这可能解释了归一化初始化或软标记效果更明显。

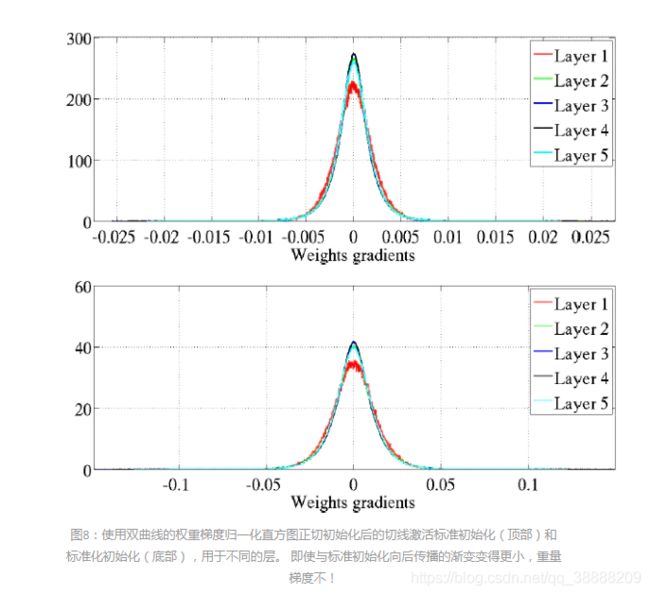
表1：具有不同激活功能和测试错误的测试错误，具有5个隐藏层的深度网络的初始化方案。N在激活功能名称之后指示使用的标准化初始化。 粗体结果是统计学上的与零假设检验下的非粗体不同与p = 0.005。‘

训练后的自动编码器进行无监督预训练（Vincent et al。，2008），从初始化获得监督微调的误差曲线。对于每个网络，分别选择学习率来最小化验证集上的错误。我们可以指出，在Shapeset-3×2上，由于任务的困难，我们在学习过程中观察到重要的饱和度，这可能解释了归一化初始化或软标记效果更明显。从这些误差曲线中可以得出几点结论：•更经典的具有S形或双曲线正切单位的经典神经网络和标准初始化费用相当差，收敛速度更慢，并且显然趋向于最终较差的局部最小值。 •softsign网络似乎比初始化过程更稳健，可能是因为它们的温和非线性。 •对于tanh网络，建议的标准化初始化可能非常有用，大概是因为层到层转换保持了大小的

其他方法可以缓解学习期间图层之间的差异，例如利用二阶信息为每个参数单独设置学习速率。例如，我们可以利用Hessian的对角线（LeCun et al。，1998b）或梯度方差估计。这两种方法都已经应用于具有双曲正切和标准初始化的Shapeset-3×2。我们观察到性能有所增加，但没有达到标准化初始化的结果。另外，通过将归一化初始化与二阶方法相结合，我们观察到进一步的收益：估计的Hessian可能会关注单元之间的差异，而不必纠正层之间的重要初始差异。在所有报道的实验中，我们使用了每层相同数量的单位。但是，我们验证了当层大小随层编号增加（或减小）时，我们获得相同的增益。本研究的其他结论如下：训练迭代是理解深网训练困难的有力调查工具。 •当从小随机权重初始化时，应避免Sigmoid激活（不对称于0左右），因为它们产生较差的学习动态，并且最初的隐藏层饱和。 •保持层到层的转换，使得激活和梯度都能很好地流动（即雅可比矩在1左右）似乎很有帮助，并且允许纯监督的深层网络与预监督的无监督学习之间的差异的很大一部分。 •我们的许多观察结果仍未得到解释，表明进一步调查以更好地理解深层架构中的梯度和训练动态。