UCF Local Programming Contest 2015 计蒜客重现 解(补)题报告
前言
比赛时状态不是很好,差不多七道可以做的题,但是总是被一些低级失误卡很长时间(比如某处double错写成int),还有就是总会被能做出来的题目卡主,然后后面的就做不下去。所以基本功好,才能披荆斩棘一道一道AC。总的来说是自己编码水平亟待提高,有几道题超出知识范围没有补。
A - Find the Twins
题目链接
签到题
#include <iostream>
using namespace std;
int t;
int a[15];
int main()
{
int kase=0;
scanf("%d",&t);
while(t--){
int flag1=0,flag2=0;
for(int i=1;i<=10;i++){
scanf("%d",&a[i]);
if(a[i]==18) flag1=1;
if(a[i]==17) flag2=1;
}
for(int i=1;i<=10;i++) printf("%d%c",a[i],i==10?'\n':' ');
if(flag1 && flag2) printf("both\n");
else if(flag1) printf("mack\n");
else if(flag2) printf("zack\n");
else printf("none\n");
//if(t!=1)
printf("\n");
}
return 0;
}
B-
题目链接
签到题
#include <iostream>
using namespace std;
int t,a,b,c,x,y,z;
int main()
{
scanf("%d",&t);
while(t--){
int flag1=0,flag2=0;
scanf("%d%d%d%d%d%d",&a,&b,&c,&x,&y,&z);
int tot1=a+b+c,tot2=x+y+z;
if(tot1>tot2) flag1=1;
if(a>x) flag2=1;
else if(a==x){
if(b>y) flag2=1;
else if(b==y){
if(c>z) flag2=1;
}
}
printf("%d %d %d %d %d %d\n",a,b,c,x,y,z);
if(flag1 && flag2) printf("both\n");
else if(flag1) printf("count\n");
else if(flag2) printf("color\n");
else printf("none\n");
printf("\n");
}
return 0;
}
C -
题目链接
简单模拟,蛋糕数量小于等于人数时不断乘2直到大于人数,否则直接分
#include <iostream>
using namespace std;
int t,num,m,n;
int a[10000];
int main()
{
int kase=1;
scanf("%d",&t);
while(t--){
scanf("%d%d",&num,&m);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
printf("Practice #%d: %d %d\n",kase++,num,m);
for(int i=1;i<=n;i++){
while(m<=a[i]) m*=2;
printf("%d %d\n",a[i],m-a[i]);
m-=a[i];
}
printf("\n");
}
return 0;
}
D - Lemonade Stand (贪心)
题目链接
You are running a lemonade stand and have the good fortune of knowing exactly how many cups of lemonade customers are going to want to buy on each day that you run the lemonade stand. You hate to turn any customer away, so you would like to make sure that you always have enough lemons and sugar to make the appropriate number of cups of lemonade on each day. Unfortunately, the cost of lemons and sugar change daily, so you have to choose on which days you buy each, and how much of each to buy. You can buy individual lemons and five pound bags of sugar. (Note that there are 16 ounces in one pound.) On the days you choose to buy ingredients, you buy them in the morning, before any sales are made. (You’re an early riser, so you can always get to the store and back before any customers would come.) Note that you can buy as little or as much as you wish on any day to minimize your overall cost, i.e., you have enough startup money (capital) to buy as much as you wish on any day.
The Problem:
Given that you always want to have enough lemons and sugar to serve each customer, determine the minimum cost of buying those lemons and sugar.
The Input:
The first input line will have a single integer, n (1 \le n \le 100)n(1≤n≤100), the number of cases to process. The first line of each test case will have three space-separated positive integers: d (1 \le d \le 1000)d(1≤d≤1000), the number of days you’ll run the lemonade stand, x (1 \le x \le 10)x(1≤x≤10), the number of lemons needed to make a single cup of lemonade, and s (1 \le s \le10)s(1≤s≤10), the number of ounces of sugar needed to make a single cup of lemonade. The following d lines will contain data for days 1 through d, respectively. Each of these lines will have three integers separated by spaces: c (1 \le c \le 1000 ) c (1≤c≤1000), the number of cups sold for that day, pl (1 \le pl \le 50)pl(1≤pl≤50), the price of a single lemon in cents for that day, and ps (1 \le ps \le 500 ) ps (1≤ps≤500), the price of a five pound bag of sugar in cents for that day. Note that the extra sugar and lemon from each day carry over to the next day.
The Output:
For each test case, print the minimum cost of supplies (in cents) necessary to make sure that no customer who wants a cup of lemonade gets turned away.
1.题目大意:每天都要卖出一定数量的柠檬水,现在要购买柠檬和糖,每次可以买以80单位的若干糖或若干个柠檬,糖可以剩下后面接着用。接下来每天的柠檬或糖的价格可能会变化,求接下来d天每天卖出规定数量的饮料的最小进货价格
2.第一次我想到了给柠檬和糖的价格分别排序分开求,每次都买当前最小价格的那天并把后面所有天的都买掉,但是我忘记了糖如果剩余量够后面用,后面是不用买当天的糖的
3.正解就是每次记录下糖和柠檬的已出现的最小价格,柠檬直接当天的按这个价格买。但是糖要记录一个剩余量,因为是以80为单位买的,如果够就不买当天的,但是价格一定要更新
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
int x,s,d,t;
int c,pl,ps;
int main()
{
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&d,&x,&s);
ll ans=0;
int remain=0;
int min1=INF,min2=INF;
for(int i=1;i<=d;i++){
scanf("%d%d%d",&c,&pl,&ps);
min1=min(pl,min1);
min2=min(ps,min2);
ans+=x*c*min1;
int need=c*s;
if(need>remain){
need-=remain;
remain=need%80;
if(remain){
need/=80;
need++;
remain=80-remain;
}else need/=80;
ans+=need*min2;
}else remain-=need;
}
printf("%lld\n",ans);
}
return 0;
}
E - Rain Gauge(简单计算几何)
题目链接
When going to your internship you got a nice apartment with a skylight. However, one crazy party later and you now have a square-shaped hole where your skylight used to be. Rather than telling the landlord, you decided you would “fix” it by putting a circular pot to collect the water but, as the saying goes, round peg square hole. You need to determine how much of the square the circle covers to help you determine if you should buy a larger pot. Don’t worry about the area not covered; you can do multiplication and subtraction easily in your head.
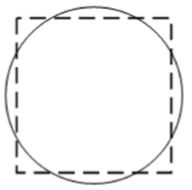
The Problem:
Given the radius of a circular pot and the length of the square skylight, calculate the amount of skylight rain area covered by the pot assuming the two shapes have the same center (i.e., are coaxial) with respect to the direction rain falls from (up). In other words, the center of the square will be directly above the center of the circle. See the picture for an example; let up be the direction from above the page, while the dotted square is the skylight and the solid circle is the pot to collect water.
The Input:
The first input line contains a positive integer, n, indicating the number of scenarios to check. Each of the following n lines contains a pair of integers, s, r (1 \le s \le 100, 1 \le r \le 100)s,r(1≤s≤100,1≤r≤100), which represents the length of the side of the skylight and the radius of the pot, respectively.
The Output:
For each scenario, output a single decimal representing the area under the skylight that is covered by the pot. Round the answers to two decimal places (e.g., 1.234 rounds to 1.23 and 1.235 rounds to 1.24). For this problem, use 3.14159265358979 as the value of pi.
1.题目大意:给出了如图所示的一个圆形和一个方形,求圆覆盖方形的面积
2.如果圆形能够覆盖方形,那么面积就是方形的面积。如果方形恰好能覆盖圆形,那么就是圆形的面积。否则就是如下图所示,我们作一条垂线,可以发现已知直角三角形的两条边,那么求出夹角θ(arccos求出的直接就是弧度),接着用扇形面积公式求扇形面积,接下来减去三角形面积就是露在外面的四个相等部分之一(下图红色部分),圆的面积减去四倍即可

#include <iostream>
#include <math.h>
using namespace std;
const double PI=3.14159265358979;
const double esp=1e-8;
int t;
double a,r;
double f(double a,double b){
return sqrt(a*a-b*b);
}
int main()
{
scanf("%d",&t);
while(t--){
scanf("%lf %lf",&a,&r);
if(r*r>=a*a/2){
printf("%.2lf\n",a*a);
}else if(r<=a/2){
printf("%.2lf\n",PI*r*r);
}else{
double o=2.0*fabs(acos((a/2)/r));
double s1=(o*r*r)/2;
double s2=f(r,a/2)*(a/2);
s1-=s2;
printf("%.2lf\n",PI*r*r-4*s1);
}
}
return 0;
}
F - Balanced Strings(字符串模拟)
题目链接
Being an individual obsessed with balancing and trying to find strings that meet that criteria, you have begun a new endeavor to study the curious structure of what we will call balanced strings. Balanced strings are strings that maintain an equal ratio of consonants to vowels in all of their substrings. What? You don’t know the difference between a consonant and a vowel? Vowels are the characters ‘a’, ‘e’, ‘i’, ‘o’, ‘u’ and sometimes ‘y’. Actually, you don’t like the character ‘y’ because this makes the problem much harder. What was the difficulty level of this problem again? Oh yeah Medium! We can’t have a problem about consonants and vowels that makes ‘y’ sometimes a vowel! That would make the problem a Hard and too many hard problems is a very bad thing. Being obsessed with balance, you have decided that ‘y’ will be included with the vowels. That way, there are 6 vowels and 20 consonants. A nice balanced even number of both! Oh! I almost forgot! A consonant is any letter that is not a vowel. Also to simplify things (this is a medium problem after all!), we will consider strings composed of lowercase letters only. Now you are ready to understand balanced strings! A balanced string is a string that has an equal number of consonants and vowels in all of its substrings. Well… not all of its substrings. Just the substrings of even length! For example, the string “orooji” has the following set of even- length substrings: {“or”, “ro”, “oo”, “oj”, “ji”, “oroo”, “rooj”, “ooji”, “orooji”}. In that set the following substrings are unbalanced: {“oo”, “oroo”, “ooji”, “orooji”}. That is, the substrings do not contain an equal number of vowels and consonants. So, the string “orooji” is not balanced. But a string like “arup” is balanced. The requisite even-length substrings are: {“ar”, “ru”, “up”, “arup”} and all these substrings are balanced (have the same number of vowels and consonants), thus the string “arup” is balanced. Note that a balanced string may contain an odd number of characters, e.g., the string “ali” is balanced since all its even-length substrings ({“al”, “li”}) are balanced. Now you want to take words and erase some of the letters and replace them with new letters to form balanced strings. Since this is a medium problem, we’ve taken the liberty of erasing some of the letters for you and replaced them with ‘?’ characters. See! The problem is already halfway solved!
The Problem:
Given a string of lowercase letters and ‘?’ characters, count the number of ways to replace all the ‘?’ with lowercase letters such that the string results in a balanced string. Two ways are considered different if there exists some i such that the i th character in one string differs from the i th character of the other string. Note that all the ‘?’ do not have to be replaced by the same letter.
The Input:
The first input line contains a positive integer, n, indicating the number of strings to balance. The strings are on the following n input lines, one string per line. Each string contains only lowercase letters and/or ‘?’ characters. Assume each input string has at least one character and at most 100 characters.
The Output:
For each string, output “String #d: v” where v is the number of ways to replace the questions marks with lower case letters. It is guaranteed that v will fit in a signed 64-bit integer for the strings we provide. Leave a blank line after the output for each string.
1.题目大意:定义一个“平衡串”:任意偶数长度的字串都既含有元音字母(比正常的a,e,i,o,u多了个y)和辅音字母,如果是?代表可以变成任意字母,求输入串可变为平衡串的个数
2.不难发现所谓平衡串就是一个元音一个辅音那样交替的字符串。那么显然分为三种情况:如果不含有?,那么之间判断是1还是0。如果都是?,那么直接判断元音个数x和辅音个数y,答案就是6x*20y+6y*20x。否则,就找到第一个非?字符的位置分别向两端扩展判断种数即可
3.自己写的时候由于用了char数组导致输入时崩溃了。但是基本思路一致,下面直接拿题解的答案敷衍
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
#define LL long long
string S;
int T,Num=0;
LL EXP(LL b,LL n){
if(n==0LL) return 1LL;
LL x=1,Power=b;
while(n){
if(n&1) x*=Power;
Power*=Power;
n>>=1;
}
return x;
}
int main(){
ios::sync_with_stdio(false);
cin>>T;
while(T--){
cin>>S;++Num;
cout<<"String #"<<Num<<": ";
int Case=-1,Len=S.size();;
for(int i=0;i<Len;++i){
if(S[i]=='?') continue;
else if(S[i]=='a' || S[i]=='e' || S[i]=='i'|| S[i]=='o' || S[i]=='u' || S[i]=='y'){
Case=i%2;
break;
}else{
Case=1-i%2;break;
}
}
if(Case==-1){
cout<<EXP(6,Len/2)*EXP(20,Len-Len/2)+EXP(20,Len/2)*EXP(6,Len-Len/2)<<endl<<endl;
continue;
}
bool flag=false;
int Count0=0,Count1=0;
for(register int i=0;i<Len;++i){
if(S[i]=='?'){
if(i%2==0) ++Count0;
else ++Count1;
}else if(S[i]=='a' || S[i]=='e' || S[i]=='i'|| S[i]=='o' || S[i]=='u' || S[i]=='y'){
if(i%2!=Case) {
flag=true;
break;
}
}else if(i%2!=1-Case){
flag=true;
break;
}
}
if(flag){
cout<<0<<endl<<endl;
continue;
}
if(Case==0) cout<<EXP(6,Count0)*EXP(20,Count1)<<endl;
else cout<<EXP(20,Count0)*EXP(6,Count1)<<endl;
cout<<endl;
}
return 0;
}
G - Towers of Hanoi Grid(棋盘规律)
题目链接
Towers of Hanoi is a rather famous problem for computer scientists as it is an excellent exercise in recursion. For those of you unfamiliar, here is the classic problem. You are given three pegs. On the first peg, there are d disks placed in decreasing order of size (as placed on the peg). The objective of the game is to move the entire tower from the first peg to the last peg. In each move, you are only allowed to move a single disk from the top of one stack to another stack. For the entire game, no disk of larger size is ever allowed to be placed on top of a disk of smaller size. The goal of the puzzle is to move the tower in the minimum number of moves.
In our problem, we will instead have an n \times nn×n grid of pegs. The rows are numbered top to bottom from 1 to n, while the columns are similarly labeled, from left to right, 1 to n. The original tower is placed on the top left peg(1,1)peg(1,1). The goal is to move the tower to the bottom right peg(n,n)peg(n,n) in the minimum number of moves possible.

Our game will have some different but related rules:For a peg(r,c)peg(r,c) at row r and column c, you may only move the top-most disk from peg (r,c)(r,c) to peg(r+1,c)peg(r+1,c) or peg(r,c+1)peg(r,c+1), in a single move and only if such a pair of pegs exists. Only pegs (1,1)(1,1) and/or (n,n)(n,n) may have more than one disk at any time; all other pegs may contain at most one disk. You can choose any peg for each move. You still may never place a larger disk on a smaller disk.
The Problem:
Given the number of disks on the starting peg and the number ndescribed above, determine the minimum number of moves to solve our Tower of Hanoi Grid puzzle.
The Input:
he first input line contains a positive integer, g, indicating the number of grids to solve. The grids are on the following ginput lines, one grid per line. Each grid is described by two integers dd and n(2 \le d \le 100, 2 \le n \le 100)n(2≤d≤100,2≤n≤100), representing the number of disks and the dimensions of the grid, respectively.
1.题目大意:有一种 Hanoi 网格游戏,游戏规则是这样的:柱子排列成棋盘,棋盘大小是 × (2 ≤ ≤ 100)。左上角的柱子上一开始有(2 ≤ ≤ 100)个圆盘,圆盘的大小从上往下依次递增。每次只能把一个圆盘移动到该柱子左边或下边的柱子,且除了左上角的柱子和右下角的柱子,每个柱子上最多同时只能有一个圆盘。右下角的柱子,大圆盘只能放在小圆盘的下面。求把左上角柱子上的圆盘全部移动到右下角的柱子上的最少移动步数
2.比赛时想到了搜索,但是没想到找规律,实际上很简单的规律题。最终肯定是中间的柱子都放上圆盘,然后依次按圆盘从大到小的顺序移动到右下角的柱子上。又因为中间的柱子上同时只能放一个圆盘,而最大的圆盘是最后一个离开左上角的柱子,第一个移动到右下角的柱子,所以中间的柱子不可能全部都放满圆盘,一定要给最大的圆盘留下一条通往右下角的路(如下图绿色部分,这些位置不能放圆盘)。容易发现,一定存在一种移动方式,使得左上角的圆盘能够从小到大地移动到灰色区域,灰色区域的圆盘又能够从大到小地移动到右下角。而且,因为只能向左和向下移动圆盘,所以每个圆盘移动到右下角的距离一定是2 × ( − 1)。所以当 ≥ × − 2 × ( − 1)时,无解。否则,答案为 × 2 ×( − 1)
#include <iostream>
using namespace std;
int n,m,t;
int main()
{
int kase=1;
scanf("%d",&t);
while(t--){
scanf("%d%d",&m,&n);
if(m>n*n-2*(n-1)) printf("Grid #%d: impossible\n",kase++);
else printf("Grid #%d: %d\n",kase++,2*m*(n-1));
printf("\n");
}
return 0;
}
I - Longest Path (哈密顿路径)
https://blog.csdn.net/qq_44691917/article/details/104562398