2020 7.30 Multi-University Training Contest 4
2020 Multi-University Training Contest 4
Blow up the Enemy
http://acm.hdu.edu.cn/showproblem.php?pid=6803
思路:儿子选择最优的策略就是用时最少的那个情况,老子等概率随机选择策略,,如果儿子与老子选的都是最优的策略则概率要乘1/2
code:
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
int ans[1100];
int main()
{
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int a,d;
for(int i=1;i<=n;i++){
cin>>a>>d;
int temp=100-a;
if(temp%a==0) ans[i]=temp/a*d;
else ans[i]=(temp/a+1)*d;
}
sort(ans+1,ans+n+1);
int num1=0,num2=0;
int x=ans[1];
for(int i=1;i<=n;i++){
if(x==ans[i]) num1++;
else num2++;
}
double res=num2*1.0/n+num1*1.0/(2*n);
printf("%.7f\n",res);
}
return 0;
}
Kindergarten Physics
http://acm.hdu.edu.cn/showproblem.php?pid=6812
思路:因为数据比较小,相当于没有里的作用,估算一下误差大约为10^-11次方,所以直接输出d即可
code:
#include
#include
#include
#define INF 0x3f3f3f3f
using namespace std;
int ans[1100];
int main()
{
int T;
cin>>T;
while(T--){
int a,b,d,t;
cin>>a>>b>>d>>t;
printf("%.7f\n",d*1.0);
}
return 0;
} Equal Sentences
思路:
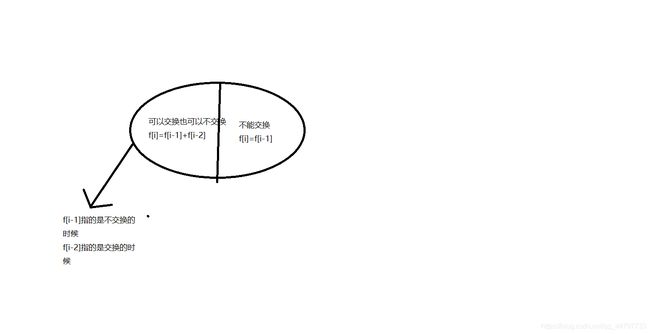
先介绍一下f[i]的含义:f[i]表示前i个单词构成的句子有多少个不同的几乎相等的句子数
这里给大家一个图
code:
#include
#include
#include
#define INF 0x3f3f3f3f
#include
using namespace std;
typedef long long ll;
//int ans[1100];
const int N=1e5+10;
const int mod=1e9+7;
ll f[N];
string s[N];
int main()
{
int t;
cin>>t;
while(t--){
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>s[i];
f[0]=f[1]=1;
for(int i=2;i<=n;i++){
if(s[i]==s[i-1]) f[i]=f[i-1];
else f[i]=(f[i-1]+f[i-2])%mod;
}
cout< Deliver the Cake
思路:建立分层图,这里是俩层,上一层L,下一层是R
然后我们开始建图:
输入边:a b c分别表示a 到b 长度为c
x为额外的代价
这里建图的时候有九种情况
1.ss[a]=='L' ss[b]=='‘R' a和b+n之间的长度为c+x(b在下层图)
2. ss[a]=='L' ss[b]=='M' 这里需要连接俩条边分别是 a与b+n之间长度是c+x(b在下层图) a与b之间的长度是c(b在上层图)
剩下情况类似
然后直接对优化dijkstra即可
code:
#include
#include
#include
#define INF 0x3f3f3f3f3f3f3f3f
#include
#include
#include
using namespace std;
typedef long long ll;
typedef pair PII;
const int N=1e5+10;
const int M=2e6+10;
int n,m,s,t,x;
char ss[N];
int head[2*N],w[M],ne[M],e[M];
int cnt;
int st[2*N];
ll dis[2*N];
void add(int a,int b,int c){
e[cnt]=b,w[cnt]=c,ne[cnt]=head[a],head[a]=cnt++;
}
void dijkstra()
{
for(int i=0;i<=2*n+1;i++) dis[i]=INF,st[i]=0;
priority_queue,greater >heap;
dis[0]=0;
heap.push({0,0});
while(heap.size()){
auto tmp=heap.top();
heap.pop();
ll ver=tmp.second,distance=tmp.first;
if(st[ver]) continue;
st[ver]=1;
for(int i=head[ver];i!=-1;i=ne[i]){
int v=e[i];
if(dis[v]>distance+w[i]){
dis[v]=distance+w[i];
heap.push({dis[v],v});
}
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--){
scanf("%d%d%d%d%d",&n,&m,&s,&t,&x);
scanf("%s",ss+1);
for(int i=0;i<=2*n+1;i++) head[i]=-1;
for(int i=0;i<=8*m+4;i++) ne[i]=w[i]=e[i]=0;
cnt=0;
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(ss[a]=='L'&&ss[b]=='R') add(a,b+n,x+c),add(b+n,a,x+c);
else if(ss[a]=='R'&&ss[b]=='L') add(a+n,b,c+x),add(b,a+n,c+x);
else if(ss[a]=='L'&&ss[b]=='M') add(a,b,c),add(b,a,c),add(a,b+n,c+x),add(b+n,a,c+x);
else if(ss[a]=='R'&&ss[b]=='M') add(a+n,b,c+x),add(b,a+n,c+x),add(a+n,b+n,c),add(b+n,a+n,c);
else if(ss[a]=='M'&&ss[b]=='L') add(a,b,c),add(b,a,c),add(a+n,b,c+x),add(b,a+n,c+x);
else if(ss[a]=='M'&&ss[b]=='R') add(a,b+n,c+x),add(b+n,a,c+x),add(a+n,b+n,c),add(b+n,a+n,c);
else if(ss[a]=='L'&&ss[b]=='L') add(a,b,c),add(b,a,c);
else if(ss[a]=='R'&&ss[b]=='R') add(a+n,b+n,c),add(b+n,a+n,c);
else if(ss[a]=='M'&&ss[b]=='M') add(a,b,c),add(b,a,c),add(a,b+n,x+c),add(b+n,a,c+x),add(a+n,b+n,c),add(b+n,a+n,c),add(a+n,b,x+c),add(b,a+n,x+c);
}
if(ss[s]=='L') add(0,s,0);
else if(ss[s]=='R') add(0,s+n,0);
else add(0,s,0),add(0,s+n,0);
if(ss[t]=='L') add(t,2*n+1,0);
else if(ss[t]=='R') add(t+n,2*n+1,0);
else add(t,2*n+1,0),add(t+n,2*n+1,0);
dijkstra();
printf("%lld\n",dis[2*n+1]);
}
return 0;
}