多层感知机与神经网络学习总结

这篇博客主要总结多层感知机（MLP）的一些知识要点，MLP也就是DNN（深度神经网络），是深度学习的基础。（原创 https://blog.csdn.net/baidu_33718858/article/details/84972537）

主要的参考文献来自于： https://machinelearningmastery.com/neural-networks-crash-course/ Jason的博客
https://www.cnblogs.com/pinard/p/6418668.html 刘建平大牛的博客，以及《深度学习》花书。

这篇博客主要包括的内容有：
0.概述
1.神经元
2.MLP的基本结构
3.前向传播算法
4.反向传播算法
5.损失函数和激活函数的选择
6.正则化

概述

人工神经网络领域通常被称为神经网络或多层感知机，可能是最有用的神经网络类型。感知机是单个神经元模型，是较大神经网络的前身。

神经网络的强大之处在于它们能够学习训练数据中的表示，以及如何将其与想要预测的输出变量联系起来。从数学上讲，它们能够学习任何映射函数，并且已经被证明是一种通用的近似算法。

神经网络的预测能力来自网络的分层或多层结构。数据结构可以选择（学会表示）不同比例或分辨率的特征，并将它们组合成更高阶的特征。例如，从线条到线条到形状的集合。

神经元

神经网络的构建块是人工神经元。

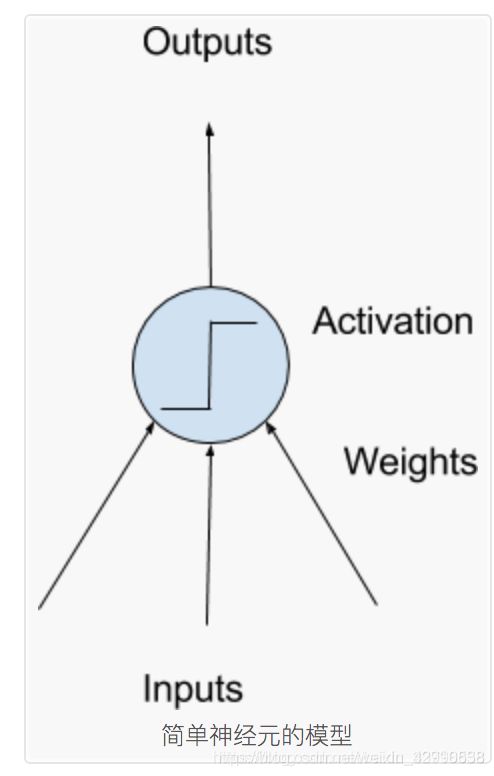
这些是具有加权输入信号并使用激活功能产生输出信号的简单计算单元。

输出和输入之间学习到一个线性关系，得到中间输出结果：

接着是一个神经元激活函数:

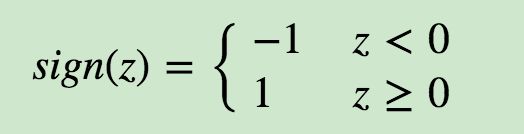
激活函数是输入加权和与神经元输出的简单映射。它被称为激活函数，因为它控制神经元被激活的阈值和输出信号的强度。
从而得到我们想要的输出结果1或者-1。

这个模型只能用于二元分类，且无法学习比较复杂的非线性模型，因此在工业界无法使用。

MLP的基本结构

神经元被排列成神经元网络，神经网络的结构是在上述的感知机结构上做了三点改进：

1）加入了隐藏层，隐藏层可以有多层，增强模型的表达能力。但同时也增加了模型的复杂度。

MLP可以理解为有很多隐藏层的神经网络，层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样。

2）输出层的神经元也可以不止一个输出，可以有多个输出，这样模型可以灵活的应用于分类回归，以及其他的机器学习领域比如降维和聚类等。

输出层中激活函数的选择受到您正在建模的问题类型的强烈约束。例如：

回归问题可能具有单个输出神经元，并且神经元可能没有激活功能。
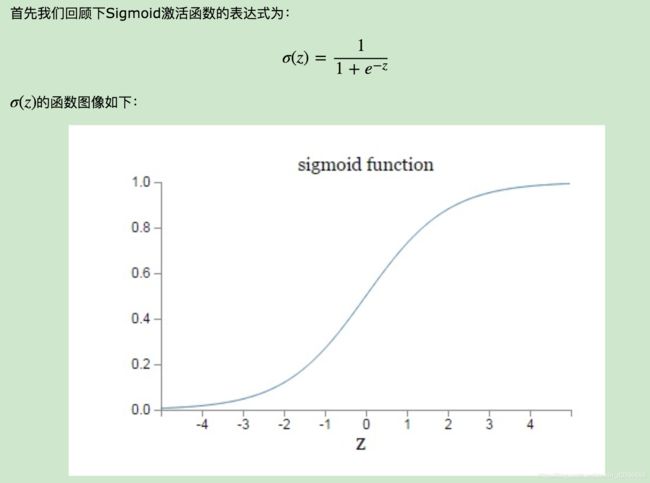
二进制分类问题可能有一个输出神经元，并使用sigmoid激活函数输出0到1之间的值，以表示预测类1的值的概率。可以通过使用阈值将其转换为清晰的类值0.5和小于阈值的捕捉值为0，否则为1。
多类分类问题可能在输出层中具有多个神经元，每个类一个（例如，在着名的虹膜花分类问题中三个类的三个神经元）。在这种情况下，softmax激活函数可用于输出网络预测每个类值的概率。选择具有最高概率的输出可用于产生清晰的类别分类值。
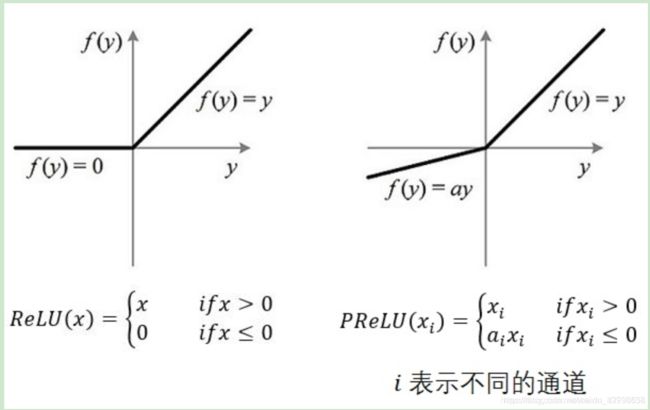
3）对激活函数做扩展，感知机的激活函数是sign(z),虽然简单但是处理能力有限，因此神经网络中一般使用的其他的激活函数。通过使用不同的激活函数，神经网络的表达能力进一步增强。

前向传播算法

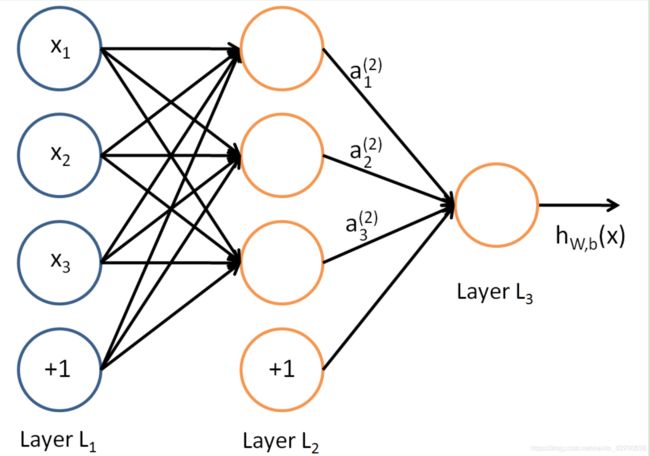
假设我们选择的激活函数是σ(z)，隐藏层和输出层的输出值为a，则对于下图的三层DNN,利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。

假设第l−1层共有m个神经元，而第l层共有n个神经元，则第l层的线性系数w组成了一个n×m的矩阵W^l, 第l层的偏倚b组成了一个n×1的向量b^l , 第l−1层的的输出a组成了一个m×1的向量a^{(l−1)，第l层的的未激活前线性输出z组成了一个n×1的向量z}l, 第l层的的输出a组成了一个n×1的向量a^l。则用矩阵法表示，第l层的输出为：

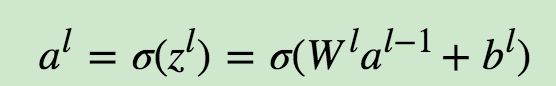
DNN的前向传播算法也就是利用我们的若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。

它是在训练网络之后使用的传递类型，以便对新数据进行预测。

反向传播算法

将网络输出与预期输出进行比较，并计算误差。然后，该错误通过网络传播回来，一次一层，并根据它们对错误的贡献量来更新权重。这个聪明的数学运算称为反向传播算法。

https://machinelearningmastery.com/implement-backpropagation-algorithm-scratch-python/ Jason的博客，讲了如何用Python 从头实现反向传播算法。https://www.cnblogs.com/pinard/p/6422831.html 刘建平的博客，重点讲了BP算法原理方面的内容。

在进行DNN反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。训练样本计算出的输出是怎么得来的？这 个输出是随机选择一系列W,b用我们上一节的前向传播算法计算出来的。因为神经网络初始化时权重和偏倚的选择随机，所以神经网络的模型是不稳定的。

使用最常见的均方差来度量损失：

算法总结如下：
损失函数和激活函数的选择

https://www.cnblogs.com/pinard/p/6437495.html 对DNN如何选择损失函数和激活函数做了总结。

均方差损失函数+Sigmoid激活函数的问题




正则化

正则化主要是针对于权重系数矩阵，可以使用常见的L1/L2正则化，通过集成学习的思想（主要是bagging的思想，训练多个DNN网络进行正则化），通过Dropout。

用得比较多的应该是Dropout，所谓的Dropout指的是在用前向传播算法和反向传播算法训练DNN模型时，一批数据迭代时，随机的从全连接DNN网络中去掉一部分隐藏层的神经元。当然，dropout并不意味着这些神经元永远的消失了。在下一批数据迭代前，我们会把DNN模型恢复成最初的全连接模型，然后再用随机的方法去掉部分隐藏层的神经元，接着去迭代更新W,b。当然，这次用随机的方法去掉部分隐藏层后的残缺DNN网络和上次的残缺DNN网络并不相同。

从上面的描述可以看出dropout和Bagging的正则化思路还是很不相同的。dropout模型中的W,b是一套，共享的。所有的残缺DNN迭代时，更新的是同一组W,b；而Bagging正则化时每个DNN模型有自己独有的一套W,b参数，相互之间是独立的。当然他们每次使用基于原始数据集得到的分批的数据集来训练模型，这点是类似的。

作者：婶婶world_peace
来源：CSDN
原文：https://blog.csdn.net/baidu_33718858/article/details/84972537
版权声明：本文为博主原创文章，转载请附上博文链接！