Codeforces 1237C2 【几何】

C2. Balanced Removals (Harder)

This is a harder version of the problem. In this version, n≤50000.

There are n distinct points in three-dimensional space numbered from 1 to n. The i-th point has coordinates (xi,yi,zi). The number of points n is even.

You’d like to remove all n points using a sequence of n2 snaps. In one snap, you can remove any two points a and b that have not been removed yet and form a perfectly balanced pair. A pair of points a and b is perfectly balanced if no other point c (that has not been removed yet) lies within the axis-aligned minimum bounding box of points a and b.

Formally, point c lies within the axis-aligned minimum bounding box of points a and b if and only if min(xa,xb)≤xc≤max(xa,xb), min(ya,yb)≤yc≤max(ya,yb), and min(za,zb)≤zc≤max(za,zb). Note that the bounding box might be degenerate.

Find a way to remove all points in n2 snaps.

Input

The first line contains a single integer n (2≤n≤50000; n is even), denoting the number of points.

Each of the next n lines contains three integers xi, yi, zi (−108≤xi,yi,zi≤108), denoting the coordinates of the i-th point.

No two points coincide.

Output

Output n2 pairs of integers ai,bi (1≤ai,bi≤n), denoting the indices of points removed on snap i. Every integer between 1 and n, inclusive, must appear in your output exactly once.

We can show that it is always possible to remove all points. If there are many solutions, output any of them.

Examples

input
6
3 1 0
0 3 0
2 2 0
1 0 0
1 3 0
0 1 0
output
3 6
5 1
2 4

input
8
0 1 1
1 0 1
1 1 0
1 1 1
2 2 2
3 2 2
2 3 2
2 2 3
output
4 5
1 6
2 7
3 8

Note

In the first example, here is what points and their corresponding bounding boxes look like (drawn in two dimensions for simplicity, as all points lie on z=0 plane). Note that order of removing matters: for example, points 5 and 1 don’t form a perfectly balanced pair initially, but they do after point 3 is removed.

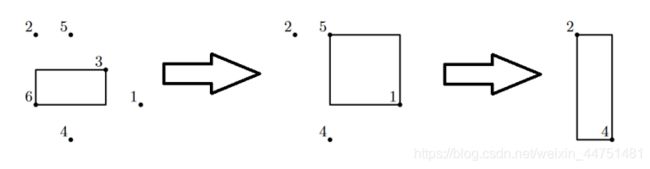
Solution

在一个三维空间上，有n个点，每次可以删两个点，前提是这两个点组成的最小区域当前已经没有别的点了。求删点的顺序。先把所有的点，根据z，y，x的优先级从小到大排序，排完序之后的点应该遵循的是，先从低到高，再从前到后，最后从左到右。先找在同一条线上最近的点，然后再找在同一个平面最近的点，最后处理完剩下的点都不在同一个平面上，找最近的即可。

Code

#include
#include
#include
using namespace std;
const int maxn = 5e4+5;

int n;
struct node {
	int x,y,z,id;
} a[maxn];
bool cmp(node a, node b) {
	if(a.z == b.z) {
		if(a.y == b.y) {
			return a.x < b.x;
		}
		return a.y < b.y;
	}
	return a.z < b.z;
}
vector<node> v;
vector<pair<int, int> > ans;

int main() {
	cin >> n;
	for(int i=1; i<=n; i++) {
		cin >> a[i].x >> a[i].y >> a[i].z;
		a[i].id = i;
	}
	sort(a+1,a+n+1,cmp);
	for(int i=1; i<=n; i++) {
		if(a[i].z == a[i+1].z && a[i].y == a[i+1].y) {
			ans.push_back(make_pair(a[i].id,a[i+1].id));
			i++;
		}
		else if(v.size() && v[v.size()-1].z == a[i].z) {
			ans.push_back(make_pair(v[v.size()-1].id,a[i].id));
			v.erase(v.end()-1);
		}
		else {
			v.push_back(a[i]);
		}
	}
	for(int i=0; i<v.size(); i+=2) {
		ans.push_back(make_pair(v[i].id,v[i+1].id));
	}
	for(int i=0; i<ans.size(); i++) {
		cout << ans[i].first << " " << ans[i].second << endl;
	}
}

Source

Codeforces 1237C2 Balanced Removals (Harder)