ACM算法总结 prufer序列

prufer序列就是一一对应一棵无根树的一个序列。

对于一棵 n 个结点的无根树，它的 prufer序列有 n-2 个数，它们之间相互转换关系如下：

• 无根树 转换为 prufer序列： 每次选择编号最小的叶子结点，然后把与它相连的结点加入 prufer序列中，然后删掉这个结点，直到剩下两个结点为止。
• prufer序列 转换为 无根树： 定义未选择的结点集合 S，一开始 S 是一个 1-n 的全集，然后遍历prufer序列，每次选择不在 prufer序列里面的最小编号的结点，与当前遍历到的结点连边，然后把当前遍历的结点从 prufer序列中删除，最后 S 中剩下的两个结点连边。

例如对于如下的一棵树：

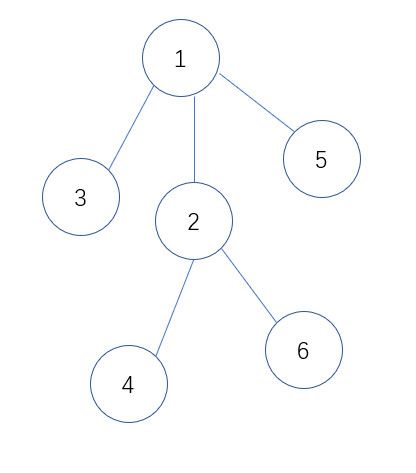
它的 prufer序列就是 1 2 1 2 。

prufer序列主要用于涉及到树的度数时的一些计数问题，它有一些重要的性质：

• 树中度数为 $d_i$ 的结点会在 prufer序列中出现 $d_i-1$ 次；
• 一棵 n 个结点的无根树（或者说一个 n 个结点的完全图的生成树）可能的数目有 $n^{n-2}$ 种，相当于 prufer序列中每个位置（总共 n-2 个位置）都由 n 中可能性；
• 对于每个结点规定度数为 $d_i$ 的树可能有 $\frac{(n-2)!}{\prod _{i=1}^n(d_i-1)!}$ 种情况，这相当于，给定 n-2 个可以重复的数，进行可重排列的方案数；

用 prufer序列处理树的计数问题时，要始终明白 prufer序列和无根树是一一对应的，可以用 prufer序列唯一地表示一棵树。

比如这道例题 Valuable Forests ：一棵无根树的 value 为它所有结点的度数的平方和，一个森林的 value 为它所有树的 value 之和。现在给出 N 个结点，要求所有可能组成森林的 value 之和。

定义四个数组 f，g，F，G，它们的意义如下：

• $f(n)$ ：n 个结点组成的无根树有多少种；
• $g(n)$ ：n 个结点组成的森林有多少种；
• $F(n)$ ：n 个结点组成的无根树的 value 之和；
• $G(n)$ ：n 个结点组成的森林的 value 之和

那么有如下四个式子成立：

• $f(n)=n^{n-2}$ ，这个是由 prufer 序列可以得知的；
• $g(n)=\sum _{i=0}^{n-1}{C}_{n-1}^{i}f(i+1)g(k-i-1)$ ，它的意义是，取 i+1 个结点组成一棵无根树，剩下的组成森林；
• $F(n)=n\sum _{d=1}^{n-1}{d}^2{C}_{n-2}^{d-1}(n-1{)}^{n-d-1}$ ，它的意义是，因为每个结点的贡献都是一样的，所以前面乘 n 之后就只用考虑其中一个结点的贡献，然后枚举这个结点的度，对于度 d，它的贡献为 $d^2\times 树的数目$ ，这个结点在 prufer 序列中应该占据 $d-1$ 个位置，然后后面那一块就是其它位置的可能数目；
• $G(n)=\sum _{i=0}^{n-1}{C}_{n-1}^i(F(i+1)g(n-i-1)+G(n-i-1)f(i+1))$ ，它的意义是，取 i+1 个结点组成一棵无根树，然后剩下的组成森林，括号中的两部分分别是无根树和森林的贡献。

这样就可以计算出来了。

代码：

#define DIN freopen("input.txt","r",stdin);
#define DOUT freopen("output.txt","w",stdout);
#include 
#include 
#define mem(a,b) memset(a,b,sizeof(a))
#define REP(i,a,b) for(int i=(a);i<=(int)(b);i++)
#define REP_(i,a,b) for(int i=(a);i>=(b);i--)
#define pb push_back
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<LL,LL> P;
int read()
{
    int x=0,flag=1; char c=getchar();
    while((c>'9' || c<'0') && c!='-') c=getchar();
    if(c=='-') flag=0,c=getchar();
    while(c<='9' && c>='0') {x=(x<<3)+(x<<1)+c-'0';c=getchar();}
    return flag?x:-x;
}

const int maxn=5005,N=5000;
LL M;
LL f[maxn],g[maxn],F[maxn],G[maxn];
LL jie[maxn],jie_[maxn];

LL ksm(LL x,LL n)
{
    LL ret=1;
    while(n)
    {
        if(n&1) ret=ret*x%M;
        x=x*x%M;
        n>>=1;
    }
    return ret;
}

LL C(LL n,LL m)
{
    if(n<m) return 1;
    return jie[n]*jie_[m]%M*jie_[n-m]%M;
}

int main()
{
    int T=read(); M=read();
    jie[0]=1;
    REP(i,1,N) jie[i]=jie[i-1]*i%M;
    REP(i,0,N) jie_[i]=ksm(jie[i],M-2);
    f[0]=0; f[1]=1; f[2]=1;
    REP(i,3,N) f[i]=ksm(i,i-2);
    g[0]=g[1]=1;
    REP(k,2,N)
    {
        REP(i,0,k-1) g[k]+=C(k-1,i)*f[i+1]%M*g[k-i-1]%M;
        g[k]%=M;
    }
    REP(k,1,N)
    {
        REP(d,1,k-1)
            F[k]+=1ll*d*d%M*C(k-2,d-1)%M*ksm(k-1,k-d-1)%M,F[k]%=M;
        F[k]%=M; F[k]*=k; F[k]%=M;
    }
    //G[0]=G[1]=1;
    REP(k,1,N)
    {
        REP(i,0,k-1)
            G[k]+=C(k-1,i)*(F[i+1]*g[k-i-1]%M+G[k-i-1]*f[i+1]%M)%M,G[k]%=M;
    }

    while(T--)
    {
        int n=read();
        printf("%d\n",G[n]);
    }

    return 0;
}