TFHE：环面上全同态加密方案学习笔记1

全同态加密

首先简要介绍一下什么是全同态加密：同态加密是上世纪80年代提出来的一种密码学技术：对经过同态加密的数据进行处理得到一个输出，将这一输出进行解密，其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。
传统加密大致有密钥生成、加密、解密三个关键步骤：

同态加密相比传统加密最核心的部分在于它的 评估操作(Evaluation) 使得对加密的密文进的运算相当于对对应的明文进行了运算。

如果这个函数 f 是加法，则称这个同态加密是加同态，如果这个函数 f 是乘法，则称这个同态加密是乘同态。加同态和乘同态都是半同态。如果一个算法能够同时满足加法同态和乘法同态，那么我们称之为全同态算法。2009年Gentry首次提出了基于理想格的全同态加密算法，称之为[Gentry09]或[Ge09]。

全同态算法应用之一：外包计算。

全同态加密允许在不知道数据（加密）的情况下对数据进行计算，这使得用户可以将自己需要计算的数据同态加密后加密发送给云，云能够在同态加密的数据上进行计算，随后将结果（密文）返回给用户，用户解密得到计算结果。

TFHE与全同态

全同态算法在2013年左右大致分为两个大类，一类为 BGV方案，另一类为 GSW方案，而TFHE属于类GSW分支，并且是FHEW方案的一个改进，TFHE方案是目前最快的全同态加密方案。

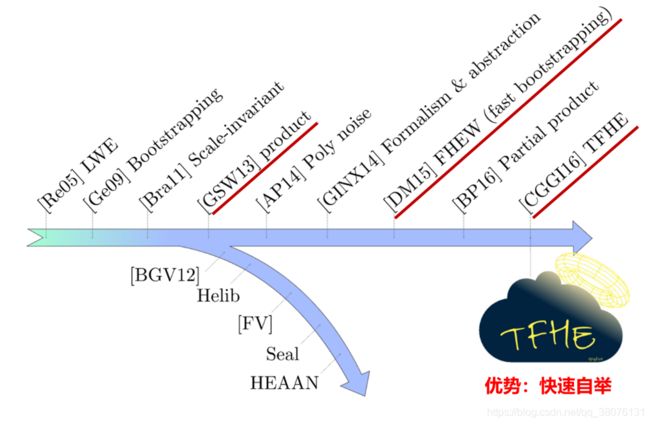
全同态加密中的噪声

众所周知，全同态加密是有噪声(error)的。假设有一布尔电路如下图：

在明文状态下评估该布尔电路，没有任何问题：
然而，在若要在全同态加密的密文状态下评估该布尔电路(这里给你一个神奇的透视镜，让你能够看到加密密文里面加密的明文，越清晰说明噪声越小，越模糊说明噪声越大)，不但评估时间变得十分漫长，噪声也随着经过的门电路的数量增加而增长，如果经过过多的门电路，则很可能导致最终的解密错误(解密后无法分辨0和1)。

想要解决同态加密中的噪声问题，目前有如下两种途径：

1. LHE 层级全同态
   通过设置LHE中的安全参数，使之足够大从而支持一定深度(depth)的布尔电路的评估。
   想象上图中最左端的密文全都有3个level，密文每通过一个 与/或门 就会消耗一个level(取非操作相比于 与/或门 产生可忽略的噪声)，如果最终的level小于0则密文不能够正确解密，如下图所示：
   
2. Bootstrapping 自举
   2009年Gentry提出了自举的最naïve的设想。整个自举过程如下：
   
   1.现有一明文m。
   2.使用$p{k}_1$对该明文进行加密，得到一个密文，此时密文新鲜(fresh)，噪声较小。假设如果噪声不超过框中的红线，就可以正确地进行解密。
   3.经过一系列的评估操作之后，噪声不断增大，现在噪声已经达到红线，必须将噪声减小才能继续进行计算。最直观地方法就是对其进行解密，因为解密之后噪声会消失，但是解密需要密钥，如果这个过程在云服务器上执行的话客户端是不可能给出自己的私钥的。
   4.于是Gentry想了一个办法，他将解密函数Dec作为评估函数中的f，再用一个新的公钥$p{k}_2$将整个密文加密，用户的私钥$s{k}_1$(对应公钥$p{k}_1$)也使用$p{k}_2$进行加密后给云服务器。
   5.这时候云服务器就可以在$p{k}_2$加密下进行同态解密，从而得到$p{k}_2$加密的f(m)，此时噪声比之前少了许多，能够支持至少一次的乘法运算。
   通过这样的自举步骤，同态加密的运算便能够不断地持续地进行。

LHE 和 Bootstrapping 两种方案各有优缺点：

层次全同态(LHE)	层次全同态(LHE)	自举(Bootstrapping)	自举(Bootstrapping)
优点	缺点	优点	缺点
在深度(depth)小的电路上很快	在很深的电路中不现实	深度没有限制	非常非常非常慢
	不能实现不事先知道电路深度的电路		密钥很大

TFHE在 LHE 方案和 Bootstrapping 方案中都实现了一定的改进，接下来详细介绍TFHE。

TFHE

Torus 环面

TFHE全称为：Fully Homomorphic Encryption over the Torus。FHE代表全同态加密，而T代表环面(Torus)。因此，想了解TFHE，在了解什么是FHE后，还要了解什么是环面。
环面大概长下面这张图的样子，像一个甜甜圈(by Ilaria Chillotti)：

实数环面 The real torus $\mathbb{T}=\mathbb{R}/\mathbb{Z}=\mathbb{R}mod1$
我们把一个实数环面记为($\mathbb{T},+,\cdot )$的形式$(\cdot :\mathbb{Z}\times \mathbb{T}\to \mathbb{T}$ a valid external product)。括号中的$\mathbb{T}$表示数据是环面里面的结构，$+$和$\cdot$两种运算(或者说两种映射)。其中$+$(加法)类似我们平时用的加法，$\cdot$(数乘)是一个从$\mathbb{Z}$和$\mathbb{T}$到$\mathbb{T}$的映射(外积)，这里的$\mathbb{Z}$表示整数集。
下面我用蓝色表示环面$\mathbb{T}$里面的元素，用红色表示整数域$\mathbb{Z}$里面的元素。
实数环面有三条性质：

1. 它是一个阿贝尔群(环面上的加法是有定义的)。
2. 它拥有 $\mathbb{Z}$-module 结构。
3. 它不是一个环(环面上的元素之间的乘法没有定义)。

我们可以把实数的环面扩展到n维向量或矩阵空间：(${\mathbb{T}}^n,+,\cdot$)，它同样拥有 Z-module 结构。

我们还可以定义多项式环面：(${\mathbb{T}}_N[X],+,\cdot$)，它有 $\mathfrak{R}$-module 的结构(其中$\mathfrak{R}=\mathbb{Z}[X]/(X^N+1),{\mathbb{T}}_N[X]=\mathbb{T}[X]mod(X^N+1)$)。下面用红色表示$\mathfrak{R}$中元素：

TLWE密文的对称加密

加密步骤：

1. 假设消息空间 $M=\{0,1/3,2/3\}$ 是实数环面上逆时针三元消息空间。
2. 假设现在要加密明文消息 $\mu =1/3mod1\in M$。
3. 现在给消息添加一个高斯噪声：计算phase：$\phi =\mu +Gaussianerror$。
4. 然后在环面上随机选择一个$a$作为mask(当$a=0$时为平凡(trivial)的情况，此时明文与密钥相互独立，没有加密的效果)。
   
5. 随后可以使用密钥s进行加密，得到密文：$b=s\cdot a+\phi$(LWE形式，安全性基于LWE问题的困难性)。加密后的密文$b$看起来像一个随机数。
6. 同样也可以使用密钥s进行解密，得到phase：$\phi =b-s\cdot a$，再对phase进行取整(round)到最近的消息空间中的元素(也可以求期望)，最终可得到消息$\mu$。
   

这虽然是LWE困难问题，却没有LWE中的 mod $q$ 操作(实数环中 mod 1)。
TLWE密文具有同态性质，在密文上进行线性组合，其对应明文也会做相应的线性组合，噪声也随之增加。换句话说，我们对TLWE上的元素做一个线性组合，那它们的$a$和$b$也会有相应的线性关系，如果我们把它解密，$\phi$也会有同样的关系。因为我们添加的噪声是高斯噪声，我们对$\phi$求平均得到消息$\mu$，也会满足这个关系。这是环面上自带的加同态的性质，对于全同态加密的设计来说是一个很好的性质。

TFHE的三种密文形式

除TLWE密文外，TFHE方案中还有两种密文：TRLWE密文与TGSW密文。将TLWE拓展到多项式环面，可得TRLWE密文，将GSW方案拓展至环面，可得TGSW密文。接下来给出TFHE三种密文格式的定义：

• TLWE 密文：$c=(a,b)\in {\mathbb{T}}^{n+1}$
  其中 $b=s\cdot a+\phi ,\phi =e+\mu$
• TRLWE 密文：$c=(a,b)\in {\mathbb{T}}_N[X{]}^2$
  其中 $b=s\cdot a+e+\mu ,e\in {\mathbb{T}}_N[X]Gaussian$
• TRGSW 密文：$C=Z+m\cdot G_2\in {\mathbb{T}}_n[X{]}^{2l\times 2}$
  其中 $Z$ 为长 $2l$ 的一列0的RLWE加密，$G_2$为 gadget 矩阵。

给一个直观的感受：

下面给出三种密文的明文、密文和密钥的形式，以及可以进行的运算：

名称	明文	密文	线性组合	product	密钥
TLWE	$\mathbb{T}$	${\mathbb{T}}^{n+1}$	$\surd$	$\times$	${\mathbb{B}}^n$
TRLWE	${\mathbb{T}}_N[X]$	${\mathbb{T}}_N[X{]}^2$	$\surd$	$\times$	${\mathbb{B}}_N[X]$
TRGSW	$\mathbb{Z}[X]/(X^n+1)$	${\mathbb{T}}_N[X{]}^{2l\times 2}$	$\surd$	$\surd$	${\mathbb{B}}_N[X]$

TFHE的外积加速

我们发现TLWE密文和TRLWE密文只能进行线性组合，不能进行Product(积)的操作，即只能做加法不能做乘法。TFHE的研究者在定义了TLWE密文和TRLWE密文后，觉得好像离全同态加密还差一点，于是他们从GSW方案中找到了灵感。GSW方案中有一个ring product(内积)的操作：
输入是两个TGSW samples，$\mathbb{Z}[X]$是整数多项式，输出是一个TGSW sample，解密后得到两个消息的乘积，噪声小于等于 $\Vert {\mu }_A\Vert {\eta }_B+O({\eta }_A)$。这里观察到，尽管运算是对称的，但是它产生的噪声是不对称的。TFHE的研究者基于这个特性研究出了TFHE：把其中一个输入换成TLWE类型，然后输出也变成了TLWE类型，计算变成了点乘(外积)。

噪声本来就不对称，现在更不对称了(更小了)。然后便可以用分解的方法，把原来TGSW的每行拆开，在并行计算，将原来的叉乘(内积)都变成了点乘(外积)，得到一个很大的提速。

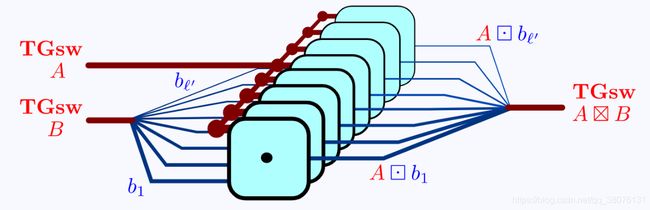
下面给出内积和外积的具体表达式以及直观的感受：

层次TFHE(TFHE IN LEVELED MODE)

这一部分使用层次TFHE实现一个确定型自动机的评估。使用上面所说的同态外积构造门：

设TGSW密文的消息空间为 $\{0,1\}\in \mathbb{Z}[X]$，TLWE密文的消息空间为$\{0,1/2\}\in \mathbb{T}[X]$，这样噪声中的$||{\mu }_A|{|}_1$就没有了(为1)。
接下来为TFHE选择门电路，这里给出四种图灵完备的门电路组合：

1. Or, And, Not
   DNF logic
2. Xor, And, 1
   Multivariate polynomials
3. Nand
   minimal indeed
4. Mux, 0, 1
   Because we get binary decision diagrams for free

在LHE里面通常选择Xor这一组，FHEW选择了与非门，而(level)TFHE选择的是Mux电路，因为它可以几乎没有消耗的做二进制选择(噪声呈线性增长)。
Mux门电路的选择逻辑很简单，如果c为0则输出b，如果c为1则输出a：
$$CMux(c,a,b)=b+c⊡(a-b)$$

在(level)TFHE的Mux门电路中有不同的线：图中深红色的线成为控制线(Control line)，传输TGSW密文，蓝色的先称为数据线(data line)，传输TLWE密文。
随后，我们便可以使用Mux门电路构造和评估任意的 查找表/布尔函数(噪声随电路深度的增加线性增长)：

进而可以评估(输入长度已知并固定的)任意确定型(有穷)自动机：

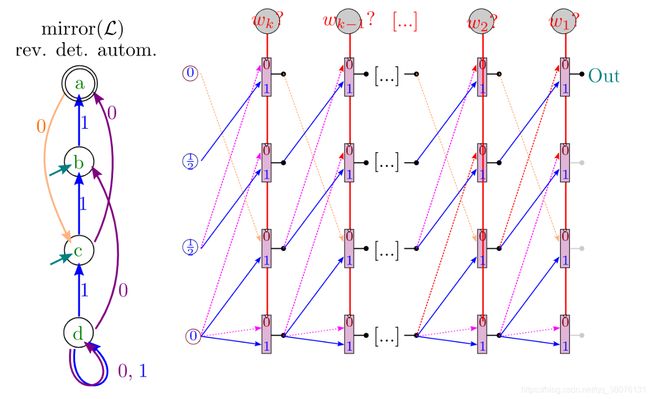
全同态TFHE(TFHE IN FHE MODE)

为实现任意深度电路的同态评估，需要为TFHE引入自举(bootstrapping)操作。
自Gentry于2009年提出自举以来，自举从同态解密(Gentry09)，到重加密，到压缩解密函数，再到密钥交换&模交换(FHEW&TFHE使用)。在Gentry09的自举(前面有写)中，自举是一个单独的函数，仅用于减小噪声；而在TFHE中，自举可以改变消息内容。接下来介绍TFHE中的自举门(gate bootstrapping)。
我们现在有一个二进制的消息空间，消息只有false和true。设false是$-1/8(-1/8=7/8)$，噪声小于$1/16$，设true是$1/8true($1/8)$，噪声也小于$1/16$。现在再给你一副神奇的眼镜，让你能够看到LWE加密下的明文。

然后我们把两个环面相加。它们的值可能是真或假。如果他们都是假，那会得到$3/4$(红色)，如果他们一真一假，会得0(黄色)，如果他们都是真，得到$1/4$(绿色)。：

在能够看到明文的条件下，如何进行自举的与非操作呢？非常简单，我们把这个环面画一条线，落在线的左边就输出true，落在右边就输出false：

难点在于我们如何在密文(摘掉你的神奇眼镜)下进行操作。TFHE给出了这样的答案：

1. 首先从一个(平凡的)TLWE$(v_0+v_{1}X+\dots +v_{(}N-1)X^{(}N-1){)}^a$开始
2. 将其旋转$p=-{\phi }_s(a,b)$个位置
3. 取出常数项constant term(其加密$v_p$)

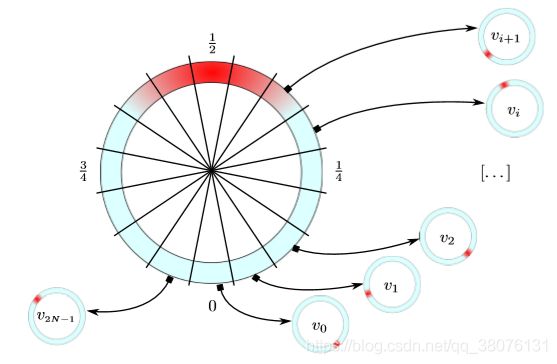
最困难的部分在第2步。将环面旋转$p$个位置有两种情况：
在$p$已知的情况下，旋转操作为$(X^p\cdot c)$。
在$p$未知的情况下，旋转操作为$(TGSW(X^p)⊡c)$。
那么，如何在未知s(私钥)的情况下，旋转$-{\phi }_s(a,b)=-b+{\sum }_{i=1}^n{a}_i{s}_i$个位置呢？

1. 首先反方向旋转$b$个位置，即Multiply by $X^{-b}$，$b$为密文，事先知道可以直接计算。
2. For $i\in [1,n]$ multiply by $TGSW(X^{-a_i{s}_i})$
   $X^{a_i{s}_i}=1+(X^{a_i}-1)\cdot s_i,s_i\in \{0,1\}$
   $TGSW(X^{a_i{s}_i})=h+(X^{a_i}-1)\cdot TGSW(s_i),BK=TGSW(s_i)$
   私钥$s$事先未知，将其变为公钥$BK$(Bootstrapping Key)。

完成这两部就能够完成这个旋转的任务。正确性和安全性本文不作证明。
总结自举算法：
Input:

• Anticyclical parameters $v_0,...,v_{2N-1}\in \mathbb{T}$
• A LWE sample $(a,b)$ rescaled on $\mathbb{Z}/2N\mathbb{Z}$
• {\color{red}Some encryptions} of its secret key $s\in \{0,1{\}}^n$

Output:

• An encryption of $v_{\phi }$ where $\phi =b-{\sum }_{a_i{s}_i}mod2N$

Algorithm:

1. Setup($v$)
2. PlainRotate by $X^{-b}$ positions
3. for i = 1 to n
   EncRotate by $TGSW(X^{a_i{s}_i})$ positions
4. Extract

主要参考论文：

• Chillotti I, Gama N, Georgieva M, et al. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds[C]//international conference on the theory and application of cryptology and information security. Springer, Berlin, Heidelberg, 2016: 3-33.
• Chillotti I, Gama N, Georgieva M, et al. Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 377-408.

本文仅供个人学习使用