目标检测之Yolov4

从2018年Yolov3年提出的两年后，在原作者声名放弃更新Yolo算法后，俄罗斯的Alexey大神扛起了Yolov4的大旗。（2020年提出）
Yolov4: Optimal Speed and Accuracy of Object Detection
参考链接

YOLOV 3 回顾

Yolov3是2018年发明提出的，这成为了目标检测one-stage中非常经典的算法，包含Darknet-53网络结构、anchor锚框、FPN等非常优秀的结构。

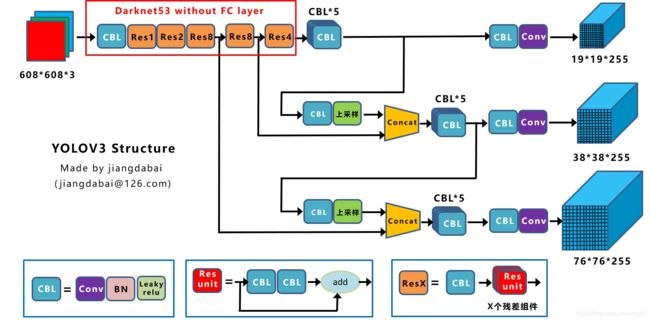
网络结构可视化

基本组件

上图三个蓝色方框内表示Yolov3的三个基本组件：

• CBL：Yolov3网络结构中的最小组件，由Conv+Bn+Leaky_relu激活函数三者组成。
• Res unit：借鉴Resnet网络中的残差结构，让网络可以构建的更深。
• ResX：由一个CBL和X个残差组件构成，是Yolov3中的大组件。每个Res模块前面的CBL都起到下采样的作用，因此经过5次Res模块后，得到的特征图是608->304->152->76->38->19大小。

其他基础操作

• Concat：张量拼接，会扩充两个张量的维度，例如2626256和2626512两个张量拼接，结果是2626768。Concat和cfg文件中的route功能一样。
• add：张量相加，张量直接相加，不会扩充维度，例如104104128和104104128相加，结果还是104104128。add和cfg文件中的shortcut功能一样。

Backbone中卷积层的数量

每个ResX中包含1+2xX个卷积层，因此整个主干网络Backbone中一共包含1+（1+2x1）+（1+2x2）+（1+2x8）+（1+2x8）+（1+2x4）=52，再加上一个FC全连接层，即可以组成一个Darknet53分类网络。不过在目标检测Yolov3中，去掉FC层，不过为了方便称呼，仍然把Yolov3的主干网络叫做Darknet53结构。

网络结构详细可视化

如下图以416x416x3输入为例

YOLOV 4

网络结构

Yolov4的结构图和Yolov3相比，多了CSP结构，PAN结构

yolov4的五个基本组件：

• CBM：Yolov4网络结构中的最小组件，由Conv+Bn+Mish激活函数三者组成。
• CBL：由Conv+Bn+Leaky_relu激活函数三者组成。
• Res unit：借鉴Resnet网络中的残差结构，让网络可以构建的更深。
• CSPX：借鉴CSPNet网络结构，由三个卷积层和X个Res unint模块Concate组成。
• SPP：采用1×1，5×5，9×9，13×13的最大池化的方式，进行多尺度融合。

其他基础操作

• Concat：张量拼接，维度会扩充，和Yolov3中的解释一样，对应于cfg文件中的route操作。
• add：张量相加，不会扩充维度，对应于cfg文件中的shortcut操作。

Backbone中卷积层的数量

和Yolov3一样，再来数一下Backbone里面的卷积层数量。
每个CSPX中包含3+2X个卷积层，因此整个主干网络Backbone中一共包含2+（3+21）+2+（3+22）+2+（3+28）+2+（3+28）+2+（3+24）+1=72。

核心内容

YoloV4的4个创新部分总述

• 输入端：这里指的创新主要是训练时对输入端的改进，主要包括Mosaic数据增强、cmBN、SAT自对抗训练
• BackBone主干网络：将各种新的方式结合起来，包括：CSPDarknet53、Mish激活函数、Dropblock
• Neck：目标检测网络在BackBone和最后的输出层之间往往会插入一些层，比如Yolov4中的SPP模块、FPN+PAN结构
• Prediction：输出层的锚框机制和Yolov3相同，主要改进的是训练时的损失函数CIOU_Loss，以及预测框筛选的nms变为DIOU_nms

输入端创新

感觉cmBN和SAT影响并不是很大，所以这里主要讲解Mosaic数据增强
Mosaic数据增强
Yolov4中使用的Mosaic是参考2019年底提出的CutMix数据增强的方式，但CutMix只使用了两张图片进行拼接，而Mosaic数据增强则采用了4张图片，随机缩放、随机裁剪、随机排布的方式进行拼接。

为什么要进行Mosaic数据增强呢？
在平时项目训练时，小目标的AP一般比中目标和大目标低很多。而Coco数据集中也包含大量的小目标，但比较麻烦的是小目标的分布并不均匀。

在整体的数据集中，小、中、大目标的占比并不均衡。
如上表所示，Coco数据集中小目标占比达到41.4%，数量比中目标和大目标都要多。
但在所有的训练集图片中，只有52.3%的图片有小目标，而中目标和大目标的分布相对来说更加均匀一些。

主要有几个优点：

• 丰富数据集：随机使用4张图片，随机缩放，再随机分布进行拼接，大大丰富了检测数据集，特别是随机缩放增加了很多小目标，让网络的鲁棒性更好。
• 减少GPU：可能会有人说，随机缩放，普通的数据增强也可以做，但作者考虑到很多人可能只有一个GPU，因此Mosaic增强训练时，可以直接计算4张图片的数据，使得Mini-batch大小并不需要很大，一个GPU就可以达到比较好的效果。

此外，发现另一研究者的训练方式也值得借鉴，采用的数据增强和Mosaic比较类似，也是使用4张图片（不是随机分布），但训练计算loss时，采用“缺啥补啥”的思路：
如果上一个iteration中，小物体产生的loss不足（比如小于某一个阈值），则下一个iteration就用拼接图；否则就用正常图片训练，也很有意思。

BackBone创新

1.CSPDarknet53
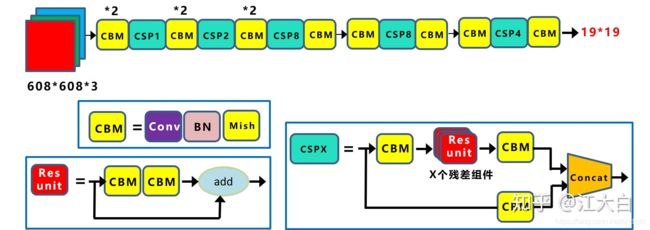
CSPDarknet53是在Yolov3主干网络Darknet53的基础上，借鉴2019年CSPNet(Cross Stage Paritial Network)的经验，产生的Backbone结构，其中包含了5个CSP模块。

**
每个CSP模块前面的卷积核的大小都是3x3，stride=2，因此可以起到下采样的作用。
因为Backbone有5个CSP模块，输入图像是608x608，所以特征图变化的规律是：608->304->152->76->38->19
经过5次CSP模块后得到19*19大小的特征图。

只在Backbone中采用了Mish激活函数，网络后面仍然采用Leaky_relu激活函数

为啥要参考2019年的CSPNet，采用CSP模块？

CSPNet全称是Cross Stage Paritial Network，主要从网络结构设计的角度解决推理中从计算量很大的问题。
CSPNet的作者认为推理计算过高的问题是由于网络优化中的梯度信息重复导致的。
因此采用CSP模块先将基础层的特征映射划分为两部分，然后通过跨阶段层次结构将它们合并，在减少了计算量的同时可以保证准确率。
因此Yolov4在主干网络Backbone采用CSPDarknet53网络结构，主要有三个方面的优点：

• 优点一：增强CNN的学习能力，使得在轻量化的同时保持准确性。
• 优点二：降低计算瓶颈
• 优点三：降低内存成本

2.Mish激活函数
Mish激活函数是2019年下半年提出的激活函数

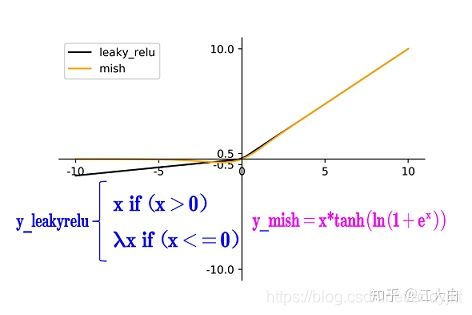
3.Dropblock

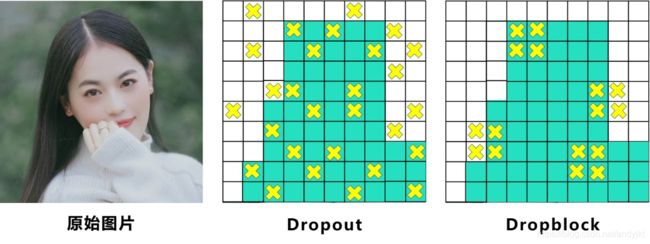
中间Dropout的方式会随机的删减丢弃一些信息，但Dropblock的研究者认为，卷积层对于这种随机丢弃并不敏感，因为卷积层通常是三层连用：卷积+激活+池化层，池化层本身就是对相邻单元起作用。而且即使随机丢弃，卷积层仍然可以从相邻的激活单元学习到相同的信息。
因此，在全连接层上效果很好的Dropout在卷积层上效果并不好。

这种方式其实是借鉴2017年的cutout数据增强的方式，cutout是将输入图像的部分区域清零，而Dropblock则是将Cutout应用到每一个特征图。而且并不是用固定的归零比率，而是在训练时以一个小的比率开始，随着训练过程线性的增加这个比率。
Dropblock的研究者与Cutout进行对比验证时，发现有几个特点：

• 优点一：Dropblock的效果优于Cutout
• 优点二：Cutout只能作用于输入层，而Dropblock则是将Cutout应用到网络中的每一个特征图上
• 优点三：Dropblock可以定制各种组合，在训练的不同阶段可以修改删减的概率，从空间层面和时间层面，和Cutout相比都有更精细的改进。

Yolov4中直接采用了更优的Dropblock，对网络的正则化过程进行了全面的升级改进。

Neck创新

1.SPP模块

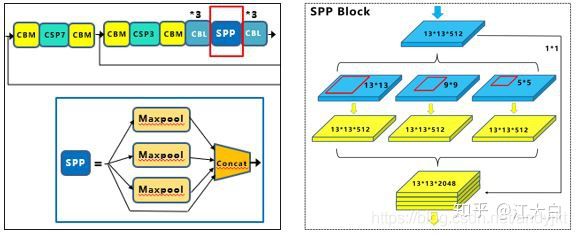
作者在SPP模块中，使用k={11,55,99,1313}的最大池化的方式，再将不同尺度的特征图进行Concat操作。
注意：这里最大池化采用padding操作，移动的步长为1，比如13×13的输入特征图，使用5×5大小的池化核池化，padding=2，因此池化后的特征图仍然是13×13大小。
采用SPP模块的方式，比单纯的使用kxk最大池化的方式，更有效的增加主干特征的接收范围，显著的分离了最重要的上下文特征。
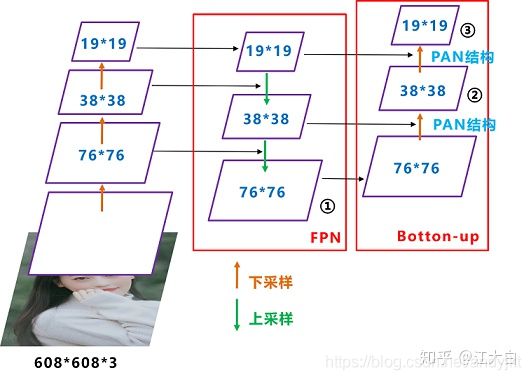
2.FPN+PAN

可以看到经过几次下采样，三个紫色箭头指向的地方，输出分别是76x76、38x38、19x19。
以及最后的Prediction中用于预测的三个特征图①19x19x255、②38x38x255、③76x76x255。[注：255表示80类别(1+4+80)×3=255]
我们将Neck部分用立体图画出来，更直观的看下两部分之间是如何通过FPN结构融合的。

FPN是自顶向下的，将高层的特征信息通过上采样的方式进行传递融合，得到进行预测的特征图。
FPN+PAN结构进行融合

其中包含两个PAN结构。

这样结合操作，FPN层自顶向下传达强语义特征，而特征金字塔则自底向上传达强定位特征，两两联手，从不同的主干层对不同的检测层进行参数聚合,这样的操作确实很皮。

FPN+PAN借鉴的是18年CVPR的PANet，当时主要应用于图像分割领域，但Alexey将其拆分应用到Yolov4中，进一步提高特征提取的能力。

注意一：
Yolov3的FPN层输出的三个大小不一的特征图①②③直接进行预测
①19x19,②38x38,③76x76
但Yolov4的FPN层，只使用最后的一个76*76特征图①，而经过两次PAN结构，输出预测的特征图②和③。
①76x76,②38x38,③19x19
输出顺序不同
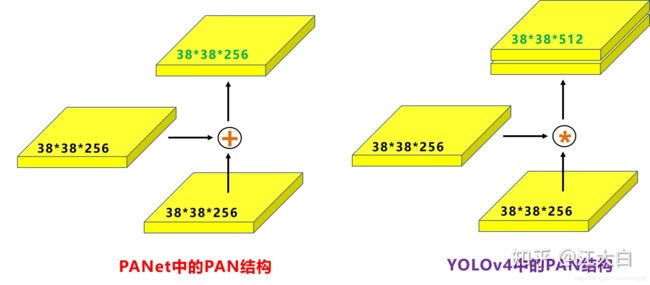
注意点二：
原本的PANet网络的PAN结构中，两个特征图结合是采用shortcut操作，而Yolov4中则采用**concat（route）**操作，特征图融合后的尺寸发生了变化。

Prediction创新

1.CIOU_loss
目标检测任务的损失函数一般由**Classificition Loss（分类损失函数）和Bounding Box Regeression Loss（回归损失函数）**两部分构成。
Bounding Box Regeression的Loss近些年的发展过程是：Smooth L1 Loss-> IoU Loss（2016）-> GIoU Loss（2019）-> DIoU Loss（2020）->CIoU Loss（2020）

我们从最常用的IOU_Loss开始，进行对比拆解分析，看下Yolov4为啥要选择CIOU_Loss。
a.IOU_Loss

可以看到IOU的loss其实很简单，主要是交集/并集，但其实也存在两个问题。

问题1：即状态1的情况，当预测框和目标框不相交时，IOU=0，无法反应两个框距离的远近，此时损失函数不可导，IOU_Loss无法优化两个框不相交的情况。

问题2：即状态2和状态3的情况，当两个预测框大小相同，两个IOU也相同，IOU_Loss 无法区分两者相交情况的不同。

因此2019年出现了GIOU_Loss来进行改进。
b.GIOU_Loss

可以看到右图GIOU_Loss中，增加了相交尺度的衡量方式，缓解了单纯IOU_Loss时的尴尬。
但为什么仅仅说缓解呢？
因为还存在一种不足：

问题：状态1、2、3都是预测框在目标框内部且预测框大小一致的情况，这时预测框和目标框的差集都是相同的，因此这三种状态的GIOU值也都是相同的，这时GIOU退化成了IOU，无法区分相对位置关系。
基于这个问题，2020年的AAAI又提出了DIOU_Loss。
c.DIOU_Loss
好的目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比。
针对IOU和GIOU存在的问题，作者从两个方面进行考虑
一：如何最小化预测框和目标框之间的归一化距离？
二：如何在预测框和目标框重叠时，回归的更准确？
针对第一个问题，提出了DIOU_Loss（Distance_IOU_Loss）

DIOU_Loss 考虑了重叠面积和中心点距离，当目标框包裹预测框的时候，直接度量2个框的距离，因此DIOU_Loss收敛的更快。

但就像前面好的目标框回归函数所说的，没有考虑到长宽比。

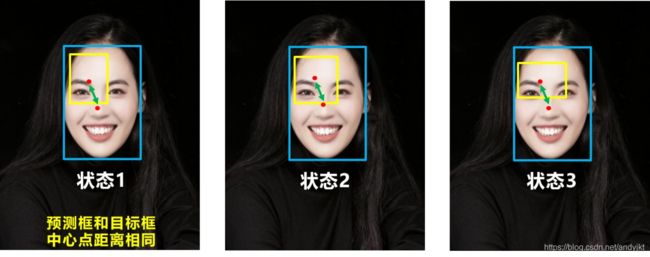
比如上面三种情况，目标框包裹预测框，本来DIOU_Loss可以起作用。
但预测框的中心点的位置都是一样的，因此按照DIOU_Loss的计算公式，三者的值都是相同的。
针对这个问题，又提出了CIOU_Loss，不对不说，科学总是在解决问题中，不断进步！！
d.CIOU_Loss
CIOU_Loss和DIOU_Loss前面的公式都是一样的，不过在此基础上还增加了一个影响因子，将预测框和目标框的长宽比都考虑了进去。

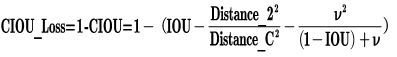
其中v是衡量长宽比一致性的参数，我们也可以定义为：

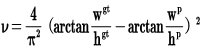
这样CIOU_Loss就将目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比全都考虑进去了。

再来综合的看下各个Loss函数的不同点：

IOU_Loss：主要考虑检测框和目标框重叠面积。

GIOU_Loss：在IOU的基础上，解决边界框不重合时的问题。

DIOU_Loss：在IOU和GIOU的基础上，考虑边界框中心点距离的信息。

CIOU_Loss：在DIOU的基础上，考虑边界框宽高比的尺度信息。

Yolov4中采用了CIOU_Loss的回归方式，使得预测框回归的速度和精度更高一些。

2.DIOU_nms
Nms主要用于预测框的筛选，常用的目标检测算法中，一般采用普通的nms的方式，Yolov4则借鉴上面D/CIOU loss的论文：https://arxiv.org/pdf/1911.08287.pdf

将其中计算IOU的部分替换成DIOU的方式：

在上图重叠的摩托车检测中，中间的摩托车因为考虑边界框中心点的位置信息，也可以回归出来。

因此在重叠目标的检测中，DIOU_nms的效果优于传统的nms。

为什么不用CIOU_nms，而用DIOU_nms?
答：因为前面讲到的CIOU_loss，是在DIOU_loss的基础上，添加的影响因子，包含groundtruth标注框的信息，在训练时用于回归。
但在测试过程中，并没有groundtruth的信息，不用考虑影响因子，因此直接用DIOU_nms即可。