双线性插值bilinear interpolation

 

线性插值，双线性插值Bilinear Interpolation算法

https://blog.csdn.net/xbinworld/article/details/65660665

https://blog.csdn.net/xjz18298268521/article/details/51220576

图像处理常用插值方法总结

https://cloud.tencent.com/developer/article/1082360

http://www.1zlab.com/wiki/python-opencv-tutorial/opencv-interpolation-algrithm/

1前言

关于中心对齐，网上找到的资料都是错的，只好参考一下自己写吧。

 

2线性插值

线性插值，即已知两点(x0,y0)，(x1,y1)和之间某点的一维坐标x，求该点的另一维y。

例如:

(x0,y0)=(2,6)，

(x1,y1)=(5,15)

求：

(x, y)=(3, ?)

公式1：斜率方式

公式2：距离比例方式

小结

两个公式结果相同，实际上两者是等价的。

 

3双线性插值法

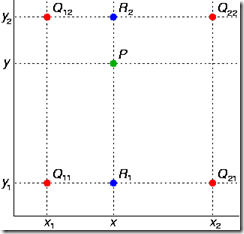
原理

双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插，如下图所示：

已知点四个：f(i,j), f(i+1,j),  f(i,j+1), f(i+1,j+1)

待求点一个：f(i+u,j+v)

图示四点是相邻的，实际上四点不相邻也没有关系。下面推导。

公式

已知：四点(x1,y1,z11)，(x2,y1,z21)，(x1,y2,z12)，(x2,y2,z22)，和之间某点的一维坐标（x，y），

求：该点的灰度z。

首先在 x 方向进行线性插值，得到

然后在 y 方向进行线性插值，得到

这样就得到所要的结果 f(x, y)，

理解

这个式子怎么理解呢？

拿第一项说。

分母实际是计算了四点围成的矩形面积。

第一项中的实际上是计算点对平均单位面积的贡献

乘数是计算了点(x,y)到的距离加权。由于越近，贡献越大，因此使用了衡量。

到这一步，是不是可以直接写出表达式了？

 

单元格内的简化

如果四点正好是单元格上的四点，则公式如下：

这种插值方法的结果通常是线性的，线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

 

4中心对齐

在成熟库中，例如opencv和matlab，通常会有中心对齐等精操作和整数计算代替float等加速。

假如要将5×5的图片resize成3×3。

   

此处参考：含python代码，只是原文是3×3转5×5

https://zhuanlan.zhihu.com/p/49832888

要通过双线性插值的方法算出dst中每一个像素点的像素值，是通过dst像素点的坐标对应到src图像当中的坐标；然后通过双线性插值的方法算出src中相应坐标的像素值。

原点对齐方法不可行

坐标对应关系：

➢按比例对应：

SrcX=(dstX)* (srcWidth/dstWidth)

SrcY=(dstY) * (srcHeight/dstHeight)

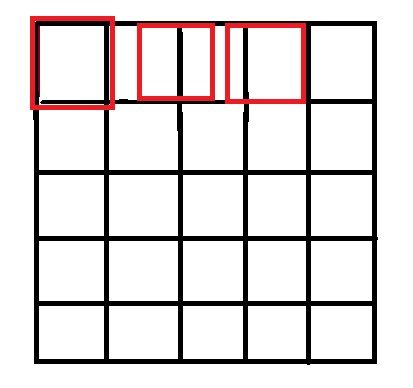
按照网上一些博客上写的，源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：

只画了一行，用做示意，从图中可以很明显的看到，如果选择右上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。

那么，让坐标加1或者选择右下角为原点怎么样呢？很不幸，还是一样的效果，不过这次得到的图像将偏右偏下。

最好的方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。

 

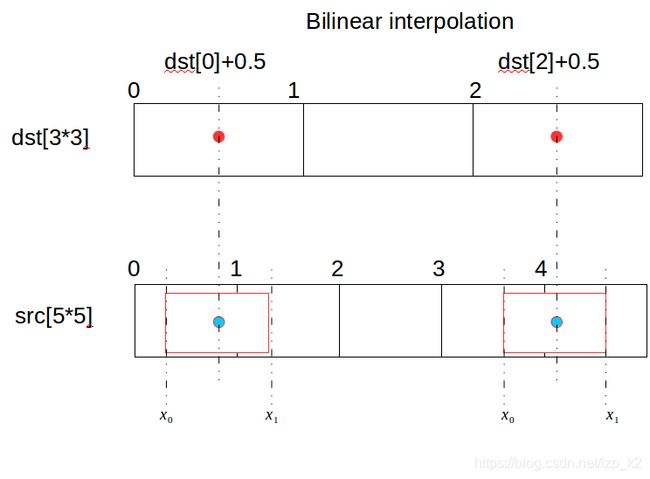
几何中心对齐：浮点坐标

计算目标图像像素的单元格的几何中心在原图上的浮点坐标。

图像双线性插值只会用相邻的4个点，只需要确定x0,x1,y0,y1即可。

下面公式以计算x0，x1为例。

src_x = (dstX+0.5)* (srcWidth/dstWidth)  # 找到目标图上像素格的几何中心在原图的浮点坐标

x0 = src_x - 0.5 # 计算中心点的左边的浮点坐标

x1 = src_x + 0.5 # 计算中心点的右边的浮点坐标

几何中心对应原理如下图所示。只画出一行示意。

左侧的红色框表示像素dst[0]的中心在src图上的左边和右边的。是浮点数。

（同理，右侧的红色框表示像素dst[2]的中心在src图上的左边和右边的。是浮点数。）

同理，按列，可以计算出上下边界y0, y1。

 

找原图上的坐标：整形坐标

以左侧边框为例，找到浮点数边界后，由于像素坐标都是整数存在的，如何找到相邻的四个坐标呢？

就是取整。

(np.floor(x0), np.floor(y0))就是点1的坐标

(np.floor(x0)+1, np.floor(y1)+1)就是点2的坐标

对应原理图，dst[0]的int[x0]即原图像素0。

但是不能超过src的边界同时坐标必须是整型，综合起来有：

src_x_0 = int(np.floor(srcX))
src_y_0 = int(np.floor(srcY))
src_x_1 = min(src_x_0 + 1, src_w - 1)
src_y_1 = min(src_y_0 + 1, src_h - 1)

即找到了四个点：(x0,y0),(x1,y0),(x0,y1),(x1,y1)。然后就可以双线性插值了。

============================================================

代码示例：

按channel循环遍历每一个坐标点：

其中

scale_x=src_x/dst_x

完整代码：

# use bilinear
def bilinear(src, dst_h, dst_w):
    src_h, src_w = src.shape[:2]
    scale_x = src_w/dst_w
    scale_y = src_h/dst_h

    channel = src.shape[2]
    dst = np.zeros([dst_h, dst_w, channel])
    for c in range(channel):
        for dst_y in range(dst_h):  # 对height循环
            for dst_x in range(dst_w):  # 对width循环
                if dst_x == dst_w-1:
                    a = 1
                # 目标在源上的坐标
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5

                # 计算在源图上四个近邻点的位置
                src_x_0 = max(int(np.floor(src_x)), 0)
                src_y_0 = max(int(np.floor(src_y)), 0)
                src_x_1 = min(src_x_0 + 1, src_w - 1)
                src_y_1 = min(src_y_0 + 1, src_h - 1)

                # 双线性插值
                value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, c] + \
                         (src_x - src_x_0) * src[src_y_0, src_x_1, c]
                value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, c] + \
                         (src_x - src_x_0) * src[src_y_1, src_x_1, c]
                dst[dst_y, dst_x, c] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)

    return dst

但是，这样处理会有黑边。

改进代码如下：

# use bilinear
def bilinear(src, dst_h, dst_w):
    src_h, src_w = src.shape[:2]
    scale_x = src_w/dst_w
    scale_y = src_h/dst_h

    channel = src.shape[2]
    dst = np.zeros([dst_h, dst_w, channel])
    for c in range(channel):
        for dst_y in range(dst_h):  # 对height循环
            for dst_x in range(dst_w):  # 对width循环
                if dst_x == dst_w-1:
                    a = 1
                # 目标在源上的坐标
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5

                # 计算在源图上四个近邻点的位置
                src_x_0 = max(int(np.floor(src_x)), 0)
                src_y_0 = max(int(np.floor(src_y)), 0)
                src_x_1 = min(src_x_0 + 1, src_w - 1)
                src_y_1 = min(src_y_0 + 1, src_h - 1)

                # 处理黑边问题(插值后边界值为0或近0)
                # 处理方式是复制边界值
                # x_0和x_1一定不能相等，同理y_0和y_1一定不能相等，否则会出现黑边
                if src_x_0 == src_x_1 and src_x_0 == src_w - 1:
                    src_x_0 = max(src_x_0-1, 0)
                if src_y_0 == src_y_1 and src_y_0 == src_h - 1:
                    src_y_0 = max(src_y_0-1, 0)

                # 双线性插值
                value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, c] + \
                         (src_x - src_x_0) * src[src_y_0, src_x_1, c]
                value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, c] + \
                         (src_x - src_x_0) * src[src_y_1, src_x_1, c]
                dst[dst_y, dst_x, c] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)

    return dst