动态规划算法--斐波拉契数列、钢条切割、小朋友过桥、01背包问题
文章目录
- 动态规划
- 1.求斐波拉契数列Fibonacci 。
- 2.钢条切割
- 3.小朋友过桥问题
- 4.01背包问题
- 购物单:有依赖的01背包问题
- 5. 最多路径数
- 6. 编辑距离
- 7. 4 键键盘问题
- 8. leetcode322. 零钱兑换
- 9. leetcode983. 最低票价
- 10. 经典算法题:高楼扔鸡蛋
- 11. leetcode 221. 最大正方形
- 12.leetcode 10. 正则表达式匹配
- 13. 最长递增子序列
动态规划
第一个基本特点:所求解的问题满足最优子结构,问题可以分解为规模更小的子问题,问题的最优解依赖于子问题的最优解。
第二个基本特点:相同的子问题只需要求解一次,如果子问题的解会被多次引用,可以将子问题的解保存起来。
*动态规划算法的核心是 一个小故事。
A * “1+1+1+1+1+1+1+1 =?” *
A : “上面等式的值是多少”
B : 计算 “8!”
A 在上面等式的左边写上 “1+” *
A : “此时等式的值为多少”
B : quickly “9!”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”
由上面 小故事可以知道动态规划算法的核心就是记住已经解决过的子问题的解。
动态规划算法的两种形式
①自顶向下的备忘录法
②自底向上。
1.求斐波拉契数列Fibonacci 。
先看一下这个问题:
Fibonacci (n) = 0; n = 0
Fibonacci (n) = 1; n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)
先使用递归版本来实现这个算法:
int fib(int n)
{
if(n<=0)
return 0;
if(n==1)
return 1;
return fib( n-1)+fib(n-2);
}
//输入6
//输出:8
先来分析一下递归算法的执行流程,假如输入6,那么执行的递归树如下:
上面的递归树中的每一个子节点都会执行一次,很多重复的节点被执行,fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文,所以空间上开销也不小。这么多的子节点被重复执行,如果在执行的时候把执行过的子节点保存起来,后面要用到的时候直接查表调用的话可以节约大量的时间。
下面就看看动态规划的两种方法怎样来解决斐波拉契数列Fibonacci 数列问题。
①自顶向下的备忘录法
i#include <iostream>
#include 备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值,在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在Memo数组中,下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会在递归fib(4)的子树了,因为fib(4)的值已经保存在Memo[4]中。
②自底向上的动态规划
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还是要计算出fib(1),fib(2),fib(3)……,那么何不先计算出fib(1),fib(2),fib(3)……,呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
#include 自底向上方法也是利用数组保存了先计算的值,为后面的调用服务。观察参与循环的只有 i,i-1 , i-2三项,因此该方法的空间可以进一步的压缩如下。
#include 一般来说由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
另外,时间复杂度为二叉树的节点个数:(2^h)-1=O(2 ^N) ,空间复杂度为树的高度:h即O(N)。
分析:递归实现的代码简洁易懂,但是需要注意的是,递归由于是函数调用自身,而函数调用是有时间和空间的消耗的,每一次函数调用,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,而往栈里压入数据和弹出数据都需要时间,因而递归实现的效率不如循环。
2.钢条切割
公司购买长钢条,将其切割为短钢条出售。为简化分析,假设切割过程本身没有成本,并且切割下来的短钢条长度都为一英寸的整数倍。下表给出了不同长度的钢条的价格。

钢条切割问题:给定一根长度为n英寸的长钢条,求最优切割方案,使得销售收益最大。注意,最优方案也有可能是完全不用切割。
长度为n英寸的钢条有2^(n-1)种切割方案,因为在距离钢条左端i (i = 1, 2, … , n-1)英寸处,我们总是可以选择切割或不切割。但是在实际求解过程中,可以不用遍历所有的切割方案,而采用某种方法可以将该问题分解为规模更小的子问题,以下是求解该问题的方法:
我们将钢条从左端切下长度为 i 的一段,其中i =1, 2, … , n,有n种切法,我们对这一段不再进行切割,该段的销售收益为Pi;
而右端剩下的长度为n-i,对这一段再进行切割,这是一个规模更小的子问题,其销售收益为Rn-i。
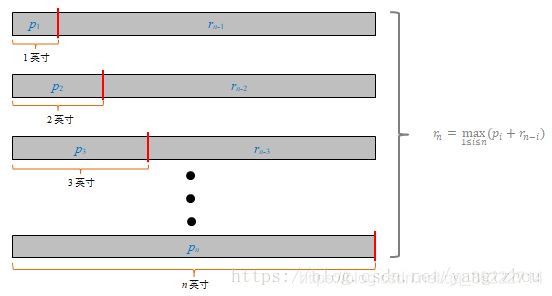
上图比较直观地展示了求解方法。显然,我们可以得到最优收益
![]()
现在使用一下前面讲到三种方法来来实现一下。
①递归版本
#include 递归很好理解,如果不懂可以看上面的讲解,递归的思路其实和回溯法是一样的,遍历所有解空间但这里和上面斐波拉契数列的不同之处在于,在每一层上都进行了一次最优解的选择,q=max(q, p[i-1]+cut(p, n-i));这个段语句就是最优解选择,这里上一层的最优解与下一层的最优解相关。
②带备忘的版本
#include有了上面求斐波拉契数列的基础,理解备忘录方法也就不难了。备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。
③自底向上的动态规划
#include动态规划原理
虽然已经用动态规划方法解决了上面两个问题,但什么时候要用到动态规划?总结一下上面的斐波拉契数列和钢条切割问题,发现两个问题都涉及到了重叠子问题,和最优子结构。
①最优子结构
用动态规划求解最优化问题的第一步就是刻画最优解的结构,如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时,用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。
②重叠子问题
在斐波拉契数列和钢条切割结构图中,可以看到大量的重叠子问题,比如说在求fib(6)的时候,fib(2)被调用了5次,在求cut(4)的时候cut(0)被调用了4次。如果使用递归算法的时候会反复的求解相同的子问题,不停的调用函数,而不是生成新的子问题。如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。在动态规划算法中使用数组来保存子问题的解,这样子问题多次求解的时候可以直接查表不用调用函数递归。
3.小朋友过桥问题
题目:在一个夜黑风高的晚上,有n(n <= 50)个小朋友在桥的这边,现在他们需要过桥,但是由于桥很窄,每次只允许不大于两人通过,他们只有一个手电筒,所以每次过桥的两个人需要把手电筒带回来,i号小朋友过桥的时间为T[i],两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。
输入:
两行数据:
第一行为小朋友个数n
第二行有n个数,用空格隔开,分别是每个小朋友过桥的时间。
输出:
一行数据:所有小朋友过桥花费的最少时间。
样例:
输入
4
1 2 5 10
输出
17
解题思路:
我们先将所有人按花费时间递增进行排序,假设前i个人过河花费的最少时间为opt[i],那么考虑前i-1个人过河的情况,即河这边还有1个人,河那边有i-1个人,并且这时候手电筒肯定在对岸,所以opt[i] = opt[i-1] + a[1] + a[i] (让花费时间最少的人把手电筒送过来,然后和第i个人一起过河)
如果河这边还有两个人,一个是第i号,另外一个无所谓,河那边有i-2个人,并且手电筒肯定在对岸,所以opt[i] = opt[i-2] + a[1] + a[i] + 2*a[2] (让花费时间最少的人把电筒送过来,然后第i个人和另外一个人一起过河,由于花费时间最少的人在这边,所以下一次送手电筒过来的一定是花费次少的,送过来后花费最少的和花费次少的一起过河,解决问题)
所以 opt[i] = min{opt[i-1] + a[1] + a[i] , opt[i-2] + a[1] + a[i] + 2*a[2] }
来看一组数据 四个人过桥花费的时间分别为 1 2 5 10
具体步骤是这样的:
第一步:1和2过去,花费时间2,然后1回来(花费时间1);
第二歩:3和4过去,花费时间10,然后2回来(花费时间2);
第三部:1和2过去,花费时间2,总耗时17。
#include 参考文章中没有考虑到边界,比如只有一个小朋友,输入1 1,应该输出1,上述代码考虑到边界。
4.01背包问题
动态规划就是一个填表的过程。该表记录了已解决的子问题的答案。求解下一个子问题时会用到上一个子问题的答案。
给定 n 种物品和一个容量为 C 的背包,物品 i 的重量是 w[i],其价值为 v[j] 。
问:应该如何选择装入背包的物品,使得装入背包中的物品的总价值最大?
算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和val[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设val[i]、 w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在面对第 i 件物品,且背包容量为 j 时所能获得的最大价值
则我们有下面的结果:
(1) v[i][0]=v[0][j]=0;//表示填入表第一行和第一列是0
(2)当w[i]>j时: v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于当前背包的容量时,就直接使用上一个单元格的装入策略
(3)当j>=w[i]时: v[i][j]=max{v[i-1][j], val[i]+v[i-1][j-w[i]]})
//当准备加入的新增的商品的容量小于等于当前背包的容量,
//装入的方式:
v[i-1][j] 就是上一个单元格的装入的最大值
val[i]:表示当前商品的价值
v[i-1][j-w[i]]:剩余空间[j-w[i]]装入i-1商品的最大值
当j>=w[i]时,取二者最大值
算法的时间复杂度分析: 优化前:O(nc)
上述算法有两个明显的缺点:其一是算法要求所给物品的重量w[i]是整数.
例:0-1背包问题。在使用动态规划算法求解0-1背包问题时,使用二维数组m[i][j]存储背包剩余容量为j,可选物品为i、i+1、……、n时0-1背包问题的最优值。绘制
价值数组v = {8, 10, 6, 3, 7, 2},
重量数组w = {4, 6, 2, 2, 5, 1},
背包容量C = 12时对应的m[i][j]数组。
如m[2][6],在面对第二件物品,背包容量为6时我们可以选择不拿,那么获得价值仅为第一件物品的价值8,如果拿,就要把第一件物品拿出来,放第二件物品,价值10,那我们当然是选择拿。m[2][6]=m[1][0]+10=0+10=10;依次类推,得到m[6][12]就是考虑所有物品,背包容量为C时的最大价值。
#include 到这一步,可以确定的是可能获得的最大价值,但是我们并不清楚具体选择哪几样物品能获得最大价值。
另起一个 x[ ] 数组,x[i]=0表示不拿,x[i]=1表示拿。
m[n][c]为最优值,如果m[n][c]=m[n-1][c] ,说明有没有第n件物品都一样,则x[n]=0 ; 否则 x[n]=1。当x[n]=0时,由x[n-1][c]继续构造最优解;当x[n]=1时,则由x[n-1][c-w[i]]继续构造最优解。以此类推,可构造出所有的最优解。
最后查看数组x,为1就表示放了
void traceback()
{
for(int i=n;i>1;i--)
{
if(m[i][c]==m[i-1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
}
x[1]=(m[1][c]>0)?1:0;
}
例,某工厂预计明年有A、B、C、D四个新建项目,每个项目的投资额Wk及其投资后的收益Vk如下表所示,投资总额为30万元,如何选择项目才能使总收益最大?
#include 购物单:有依赖的01背包问题
题目描述
王强今天很开心,公司发给N元的年终奖。王强决定把年终奖用于购物,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
主件 附件
电脑 打印机,扫描仪
书柜 图书
书桌 台灯,文具
工作椅 无
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 0 个、 1 个或 2 个附件。附件不再有从属于自己的附件。王强想买的东西很多,为了不超出预算,他把每件物品规定了一个重要度,分为 5 等:用整数 1 ~ 5 表示,第 5 等最重要。他还从因特网上查到了每件物品的价格(都是 10 元的整数倍)。他希望在不超过 N 元(可以等于 N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j 件物品的价格为 v[j] ,重要度为 w[j] ,共选中了 k 件物品,编号依次为 j 1 , j 2 ,……, j k ,则所求的总和为:
v[j 1 ]*w[j 1 ]+v[j 2 ]*w[j 2 ]+ … +v[j k ]*w[j k ] 。(其中 * 为乘号)
请你帮助王强设计一个满足要求的购物单。
输入描述:
输入的第 1 行,为两个正整数,用一个空格隔开:N m
(其中 N ( <32000 )表示总钱数, m ( <60 )为希望购买物品的个数。)
从第 2 行到第 m+1 行,第 j 行给出了编号为 j-1 的物品的基本数据,每行有 3 个非负整数 v p q
(其中 v 表示该物品的价格( v<10000 ), p 表示该物品的重要度( 1 ~ 5 ), q 表示该物品是主件还是附件。如果 q=0 ,表示该物品为主件,如果 q>0 ,表示该物品为附件, q 是所属主件的编号)
输出描述:
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值( <200000 )。
示例1
输入
复制
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出
复制
2200
考虑到每个主件最多只有两个附件,因此我们可以通过转化,把原问题转化为01背包问题来解决,在用01背包之前我们需要对输入数据进行处理,把每一种物品归类,即:把每一个主件和它的附件看作一类物品。处理好之后,我们就可以使用01背包算法了。在取某件物品时,我们只需要从以下四种方案中取最大的那种方案:只取主件、取主件+附件1、取主件+附件2、既主件+附件1+附件2。很容易得到如下状态转移方程:
f[i,j]=max{f[i-1,j],
f[i-1,j-a[i,0]]+a[i,0]*b[i,0],
f[i-1,j-a[i,0]-a[i,1]]+a[i,0]*b[i,0]+a[i,1]*b[i,1],
f[i-1,j-a[i,0]-a[i,2]]+a[i,0]*b[i,0]+a[i,2]*b[i,2],
f[i-1,j-a[i,0]-a[i,1]-a[i,2]]+a[i,0]*b[i,0]+a[i,1]*b[i,1]+a[i,2]*b[i,2]}
其中,f[i,j]表示用j元钱,买前i类物品,所得的最大值,a[i,0]表示第i类物品主件的价格,a[i,1]表示第i类物品第1个附件的价格,a[i,2]表示第i类物品第2个附件的价格,b[i,0],b[i,1],b[i,2]分别表示主件、第1个附件和第2个附件的重要度。
#include 5. 最多路径数
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
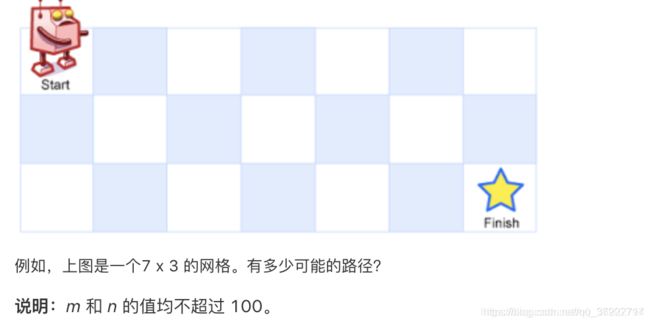
这是 leetcode 的 62 号题:https://leetcode-cn.com/problems/unique-paths/
详细解说看
https://www.cnblogs.com/kubidemanong/p/11854724.html
下面是记录一下自己的代码,方便日后查看
最初的写法
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> a1;
vector<vector<int>> a;
a1.resize(n);
a.resize(m, a1);
for (int i = 0; i < n; i++) {
a[0][i] = 1;
}
for (int i = 0; i < m; i++) {
a[i][0] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
a[i][j] = a[i - 1][j] + a[i][j - 1];
}
}
return a[m-1][n-1];
}
};
可以优化空间,因为前面计算得到的结果可以丢弃了。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n,0);
for (int i = 0; i < n; i++) {
dp[i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j]=dp[j-1]+dp[j];
}
}
return dp[n-1];
}
};
还想起另一种方式,滚动数组,就保存前一次的结果,达到压缩空间的效果。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp1(n,0);
vector<vector<int>> dp(2,dp1);
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
dp[i%2][0]=1; //这是因为每一行的第一个值都是1,实际是初始化
for (int j = 1; j < n; j++) {
dp[i%2][j]=dp[i%2][j-1]+dp[(i-1)%2][j];
}
}
return dp[(m-1)%2][n-1];
}
};
《滚动数组》—滚动数组思想,运用在动态规划当中
6. 编辑距离
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
步骤一、定义数组元素的含义
由于我们的目的求将 word1 转换成 word2 所使用的最少操作数 。那我们就定义 dp[i] [j]的含义为:当字符串 word1 的长度为 i,字符串 word2 的长度为 j 时,将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]。
步骤二:找出关系数组元素间的关系式
接下来我们就要找 dp[i] [j] 元素之间的关系了,这道题相对比较难找一点,但是,不管多难找,大部分情况下,dp[i] [j] 和 dp[i-1] [j]、dp[i] [j-1]、dp[i-1] [j-1] 肯定存在某种关系。因为我们的目标就是,从规模小的,通过一些操作,推导出规模大的。
下面分析
1、如果我们 word1[i] 与 word2 [j] 相等,这个时候不需要进行任何操作,显然有 dp[i] [j] = dp[i-1] [j-1]。(别忘了 dp[i] [j] 的含义哈)。
比如 hors--->ros,即从字符串长度4转到字符串长度3,发现word1[4] 与 word2 [3] 相等,
那么从字符串长度4转到字符串长度3不需要操作次数,实际等于从字符串长度3转到字符串长度2,所以dp[i] [j] = dp[i-1] [j-1]
2、如果word1[i] 与 word2 [j] 不相等,这个时候我们就必须进行调整,而调整的操作有 3 种,我们要选择一种。三种操作对应的关系试如下(注意字符串与字符的区别):
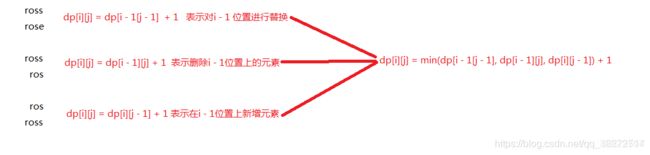
(1)、如果把字符 word1[i] 替换成与 word2[j] 相等,则有 dp[i] [j] = dp[i-1] [j-1] + 1;
比如ross-->rose,word1[4] 与 word2 [4] 不相等,
把word1[4]替换成与word2[4]相等的,就有 dp[4] [4] = dp[3] [3] + 1
(2)、如果把字符 word1[i] 删除,则有 dp[i] [j] = dp[i-1] [j] + 1;
比如ross--->ros,就等于ros--->ros再加一个删除操作
i=4 j=3 i-1=3 j=3
(3)、如果在字符串 word1末尾插入一个与 word2[j] 相等的字符,则有 dp[i] [j] = dp[i] [j-1] + 1;
比如ros--->ross,就等于ros--->ros再加一个添加操作
i=3 j=4 i=3 j-1=3
那么我们应该选择一种操作,使得 dp[i] [j] 的值最小,显然有
dp[i] [j] = min(dp[i-1] [j-1],dp[i] [j-1],dp[[i-1] [j]]) + 1;
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0]。这个还是非常容易计算的,因为当有一个字符串的长度为 0 时,转化为另外一个字符串,那就只能一直进行插入或者删除该字符串的长度。
class Solution {
public:
int minDistance(string word1, string word2) {
int m=word1.size();
int n=word2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int i=0;i<=n;i++){
dp[0][i]=i; //当一个x字符串为0时,最小编辑距离为y字符串的长度
}
for(int j=0;j<=m;j++){
dp[j][0]=j;//当一个y字符串为0时,最小编辑距离为x字符串的长度
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(word1[i-1]==word2[j-1]){
//如果 word1[i] 与 word2[j] 相等, 第 i 个字符对应字符串的下标是 i-1
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j] = min(min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1])+1;
}
}
}
return dp[m][n];
}
};
通过滚动数组来优化,一般看需要用到前的多少行,再加上当前行,1+1=2,所以%2
class Solution {
public:
int minDistance(string word1, string word2) {
int m=word1.size();
int n=word2.size();
vector<vector<int>> dp(2,vector<int>(n+1,0));
for(int i=0;i<=n;i++){
dp[0][i]=i; //当一个x字符串为0时,最小编辑距离为y字符串的长度
}
for(int i=1;i<=m;i++){
dp[i%2][0]=i; //这里也是设初值
for(int j=1;j<=n;j++){
if(word1[i-1]==word2[j-1]){
//如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
dp[i%2][j]=dp[(i-1)%2][j-1];
}else{
dp[i%2][j] = min(min(dp[(i-1)%2][j-1],dp[(i-1)%2][j]),dp[i%2][(j-1)])+1;
}
}
}
return dp[m%2][n];
}
};
参考下面
告别动态规划,连刷40道动规算法题,我总结了动规的套路
https://blog.csdn.net/shaojunbo24/article/details/47273791
7. 4 键键盘问题

如何在 N 次敲击按钮后得到最多的 A?我们穷举呗,对于每次按键,我们可以穷举四种可能,很明显就是一个动态规划问题。
这个算法基于这样一个事实,最优按键序列一定只有两种情况:
要么一直按A:A,A,…A(当 N 比较小时)。
要么是这么一个形式:A,A,…C-A,C-C,C-V,C-V,…,C-A,C-C,C-V,C-V(当 N 比较大时)。
因为字符数量少(N 比较小)时,C-A C-C C-V这一套操作的代价相对比较高,可能不如一个个按A;而当 N 比较大时,后期C-V的收获肯定很大。这种情况下整个操作序列大致是:开头连按几个A,然后C-A C-C组合再接若干C-V,然后再C-A C-C接着若干C-V,循环下去。
换句话说,最后一次按键要么是A要么是C-V。
对于「按A键」这种情况,就是状态i - 1的屏幕上新增了一个 A 而已,很容易得到结果:
// 按 A 键,就比上次多一个 A 而已
dp[i] = dp[i - 1] + 1;
刚才说了,最优的操作序列一定是C-A C-C接着若干C-V,所以我们用一个变量j作为若干C-V的起点那么j之前的 2 个操作就应该是C-A C-C了。
解释下面代码中的循环,其实就是遍历所有A,A,…C-A,C-C,C-V,C-V,…,C-A,C-C,C-V,C-V的情况,找出一种最大的值。
(我觉得 j 可以理解成C-C结束的点,往前减2,就是之前C-A操作所能得到的A的数量。
比如 i=4时, j=2时就可以考虑前面两步如果是C-A C-C的结果,j=2时是C-C,j=1时是C-A,那就是 dp[2-2]* (4-2+1)=0, dp [0]本身加上C-V两次,这是一种结果。
j还可以从3开始,j=3时是C-C,j=2时是C-A,那就是dp[3-2]*(4-3+1)=0,即dp[1]*2,dp[1]本身加上C-V一次)
int fourkey(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 0;
for (int i = 1; i <= n; i++) {
dp[i] = dp[i-1]+1;
for (int j = 2; j < i; j++) {
dp[i] = max(dp[i], dp[j - 2] * (i - j + 1));
}
}
return dp[n];
}
8. leetcode322. 零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
一开始自己的思路是先用最大的,再用次小的,测试不通过,这种是贪婪算法实现,其实并不是最优解,因为有的时候并不是要用足够大的面值,可以不同面值组合反而可以,所以放弃这种方法
//int coinChange(vector& coins, int amount) {
// int len = coins.size();
// vector dp(len, 0);
// sort(coins.begin(), coins.end());
// for (int i = len - 1; i >= 0; i--) {
// dp[i] = amount / coins[i];
// amount = amount - dp[i] * coins[i];
// }
// if (amount == 0) {
// int count = 0;
// for (int i = 0; i < len; i++) {
// count += dp[i];
// }
// return count;
// }
// else {
// return -1;
// }
//
//}
所以我们要考虑用动态规划的方法来实现
例子:假设
coins = [1, 2, 3], amount = 6

在上图中,可以看到:
F(3)=min(F(3−c1),F(3−c2 ),F(3−c3 ))+1
=min(F(3−1),F(3−2),F(3−3))+1
=min(F(2),F(1),F(0))+1
=min(1,1,0)+1
=1
确认状态
dp[0] - dp[amount] 表示构造金额amount需要的最小钞票数
确认边界状态(初始条件)
初始值设为 MAX
dp[0]=0;
状态转移方程
dp[i] = min(dp[i-1], dp[i-2], dp[i-5]) + 1
这个状态方程用下面代码实现,就是遍历coins,记录最小的
for (int j = 0; j < len; j++) {
if (coins[j] <= i) {
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
int coinChange(vector<int>& coins, int amount) {
int len = coins.size();
if (len == 0 || amount < 0) return -1;
if (amount == 0) return 0;
vector<int> dp(amount + 1, amount + 1);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int j = 0; j < len; j++) {
if (coins[j] <= i) {
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
9. leetcode983. 最低票价
在一个火车旅行很受欢迎的国度,你提前一年计划了一些火车旅行。在接下来的一年里,你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。
火车票有三种不同的销售方式:
一张为期一天的通行证售价为 costs[0] 美元;
一张为期七天的通行证售价为 costs[1] 美元;
一张为期三十天的通行证售价为 costs[2] 美元。
通行证允许数天无限制的旅行。 例如,如果我们在第 2 天获得一张为期 7 天的通行证,那么我们可以连着旅行 7 天:第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。
返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。
示例 1:
输入:days = [1,4,6,7,8,20], costs = [2,7,15]
输出:11
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 1 天生效。
在第 3 天,你花了 costs[1] = $7 买了一张为期 7 天的通行证,它将在第 3, 4, ..., 9 天生效。
在第 20 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 20 天生效。
你总共花了 $11,并完成了你计划的每一天旅行。
dp[i]表示第i天的最小钱数
如果 : 第i天没旅行,第i天的最小钱数 = 第i-1天的最小钱数
否则 : 第i天的最小钱数 = min ( 第i-1天的最小钱数+1天票钱costs[0] , 第i-7天的最小钱数+7天票钱costs[1] ,第i-30天的最小钱数+30天票钱costs[2])
其中如果 i-1,i-7,i-30<0 那天的最小钱数就为0
class Solution {
public:
int mincostTickets(vector<int>& days, vector<int>& costs) {
int len = days.size();
vector<int> dp(days.back() + 1, 0);
vector<bool> travel(days.back() + 1, false);
for (auto i : days) {
travel[i] = true;
}
dp[0] = 0;
for (int i = 1; i <= days.back(); i++) {
if (travel[i] == 0) {
dp[i] = dp[i - 1];
}
else {
if (i - 7 <= 0) {
dp[i] = min(min(dp[i - 1] + costs[0], costs[1]), costs[2]);
}
else if (i - 30 <= 0) {
dp[i] = min(min(dp[i - 1] + costs[0], dp[i - 7] + costs[1]), costs[2]);
}
else {
dp[i] = min(min(dp[i - 1] + costs[0], dp[i - 7] + costs[1]), dp[i - 30] + costs[2]);
}
}
}
return dp[days.back()];
}
};
10. 经典算法题:高楼扔鸡蛋
题目描述: (挑了一个比较严谨的描述。问题描述严谨很重要,不然会影响解题思路)
一幢 100 层的大楼,给你两个鸡蛋. 如果在第 k 层扔下鸡蛋,鸡蛋不碎,那么从前 k-1 层扔鸡蛋都不碎.
这两只鸡蛋一模一样,不碎的话可以扔无数次. 已知鸡蛋在0层扔不会碎.
提出一个策略, 要保证能测出鸡蛋恰好不会碎的楼层, 并使此策略在最坏情况下所扔次数最少.
最坏情况下所扔次数最少,比较绕口。想表达的意思是,在不明确知道哪一层会碎的情况下,要找到一种策略,通过最少的试验次数,得到临界楼层(恰好不会碎的楼层)。不明确知道,就需要考虑最糟糕的情况,而且这种策略与其他策略相比是最糟糕的情况下,最少的试验次数。
动态规划算法:
状态:
N个鸡蛋,M层楼,dp[N][M]
dp[i][j]表示i个鸡蛋,j层楼时在最坏情况下,能测出哪层楼鸡蛋不会碎。
初始状态:
N=1时,测试数为M;M=1,测试数为1;M=0,测试数为0;
状态转移方程:
如果我们一开始是在k层进行测试的
那么如果鸡蛋破碎了,我们的查找范围就变成k层以下的k-1层,当然此时鸡蛋数减少了,所以最终的步数应该为dp[i-1][k-1]+1(加1是因为我们已经操作了一次了);
另外一种情况是鸡蛋没有碎的情况,我们要找的范围变成了k层以上的,所以最终需要dp[i][j-k]+1步。
我们的目标就是要找到一个k,使得最坏情况达到,所以我们需要枚举k,然后再使得测试数最少。(max就找到最坏情况的那个楼层,min就是在这个楼层时,找到这个楼层所用的最少次数)代码如下:
#define INF 0x3f3f3f3f
int main() {
int N, M;
cin >> N >> M;
vector<int> vec1(M + 1, INF);
vector<vector<int>> dp(N + 1, vec1);
for (int i = 1; i <= N; i++) {
dp[i][1] = 1;
dp[i][0] = 0;
}
for (int i = 1; i <= M; i++) {
dp[1][i] = i;
}
for (int i = 2; i <= N; i++) {
for (int j = 2; j <= M; j++) {
for (int k = 1; k < j; k++) {
dp[i][j] = min(dp[i][j], max(dp[i - 1][k - 1] + 1, dp[i][j - k] + 1));
}
}
}
cout << dp[N][M] << endl;
}
复杂度时O(N*M^2)
参考
https://blog.csdn.net/lonelyrains/article/details/46428569
https://blog.csdn.net/fuyukai/article/details/46882603
https://mp.weixin.qq.com/s/vMks8ule7S5HHI54Be6v3A
11. leetcode 221. 最大正方形
https://leetcode-cn.com/problems/maximal-square/
动态规划
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() <= 0 || matrix[0].size() <= 0) return 0;
int row = matrix.size();
int col = matrix[0].size();
vector<vector<int>> dp(row + 1, vector<int>(col + 1, 0));
int largeedge = 0;
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= col; j++) {
if (matrix[i - 1][j - 1] == '1') {
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
largeedge = max(largeedge, dp[i][j]);
}
}
}
return largeedge * largeedge;
}
};
优化
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() <= 0 || matrix[0].size() <= 0) return 0;
int row = matrix.size();
int col = matrix[0].size();
vector<int> dp(col + 1, 0);
int largeedge = 0, pre = 0;
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= col; j++) {
int temp = dp[j];
if (matrix[i - 1][j - 1] == '1') {
dp[j] = min(min(dp[j], pre), dp[j - 1]) + 1;
largeedge = max(largeedge, dp[j]);
}else{
dp[j]=0;
}
pre = temp;
}
}
return largeedge * largeedge;
}
};
滚动数组实现
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() <= 0 || matrix[0].size() <= 0) return 0;
int row = matrix.size();
int col = matrix[0].size();
vector<vector<int>> dp(2, vector<int>(col + 1, 0));
int largeedge = 0;
for (int i = 1; i <= row; i++) {
if(dp[i%2][0] == '1')
dp[i%2][0] = 1;
for (int j = 1; j <= col; j++) {
if (matrix[i - 1][j - 1] == '1') {
dp[i%2][j] = min(min(dp[(i - 1)%2][j], dp[i%2][j - 1]), dp[(i - 1)%2][j - 1]) + 1;
largeedge = max(largeedge, dp[i%2][j]);
}else{
dp[i%2][j]=0;
//注意这一步很重要,如果当前位置不为1,就要更新它为0,和初始化步矛盾,因为是滚动数组,保存了前面的结果
}
}
}
return largeedge * largeedge;
}
};
12.leetcode 10. 正则表达式匹配
参考
https://www.cnblogs.com/mfrank/p/10472663.html
递归代码
class Solution {
public:
bool isMatch(string s, string p) {
if(p.size()<=0 && s.size() > 0) return false;
if(p.size()<=0 && s.size() <= 0) return true;
bool match = (s.size()>0 && (s[0]==p[0] || p[0] == '.'));
if(p.size()>1 && p[1]=='*'){
return isMatch(s,p.substr(2)) || (match && isMatch(s.substr(1),p));
}else{
return match && isMatch(s.substr(1),p.substr(1));
}
}
};
用一个mem存储计算过的值,可以降低复杂度,但是还是一个自顶向下计算的过程
class Solution {
public:
vector<vector<int>> mem;
bool isMatch(const string& s,const string& p)
{
mem = vector<vector<int>>(s.size() + 1, vector<int>(p.size() + 1, -1));
return doMatch(s, 0, p, 0);
}
bool doMatch(const string& s,int sIndex, const string& p, int pIndex)
{
if (mem[sIndex][pIndex] != -1)
{
return mem[sIndex][pIndex];
}
bool res;
if(pIndex >= p.size()) res = (sIndex >= s.size());
else
{
bool currentMatch = (sIndex < s.size() && (s[sIndex] == p[pIndex] || p[pIndex] == '.'));
if(pIndex+1 < p.size() && p[pIndex+1] =='*')
{
res = doMatch(s, sIndex, p, pIndex+2) || // 忽略x*
currentMatch&&doMatch(s, sIndex + 1, p, pIndex); // 如果*前的字符匹配,则将s前进一位
}
else
{
res = currentMatch&&doMatch(s, sIndex+1, p, pIndex + 1);
}
}
mem[sIndex][pIndex] = res;
return res;
}
};
自低向上的过程
class Solution {
public:
bool isMatch(const string& s, const string& p)
{
vector<vector<bool>> mem(s.size() + 1, vector<bool>(p.size() + 1, false));
mem[s.size()][p.size()] = true; //初始值
for (int i = s.size(); i >= 0; i--) {
for (int j = p.size() - 1; j >= 0; j--) {
bool match = (i < s.size() && (s[i] == p[j] || p[j] == '.'));
if (j + 1 < p.size() && p[j + 1] == '*') {
mem[i][j] = mem[i][j + 2] || (match && mem[i + 1][j]);
}
else {
mem[i][j] = match && mem[i + 1][j + 1];
}
}
}
return mem[0][0];
}
};
另外一种方法,这种方法比较符合之前做动态规划的思路
dp[i][j] 表示s的前i个字符能是否和p的前i个字符匹配,匹配就为true,否则为false
1.如果匹配 s[i-1]==p[j-1]
dp[i][j] = dp[i-1][j-1];
2.不匹配 s[i-1]!=p[j-1]
1)p[j-1]==’.’
'.‘是万能字符,可以直接让’.'等于s[i]处的字符
dp[i][j] = dp[i-1][j-1];
2)p[j-1]==’’
'‘可以匹配零个或多个前面的元素,而是否能取多个或1个字符要看j-2的字符是否和i-1的字符相同。因此首先要判断p[j-2]==s[i-1]
(2.1) p[j-2]s[i-1]||p[j-2]’.’
可以让* 代表0个字符或多个字符,如果p[j-2]为’.'就可以替换为s[i-1]的字符
如果p的*前边字符和s当前字符相等或者p的字符是‘.’
三种可能
匹配0个,比如aa, aaa * 也就是没有 * 和 * 之前的字符也可以匹配上(在你(a *)没来之前我们(aa)已经能匹配上了)dp[i][j]=dp[i][j-2]
匹配1个,比如aab aab* 也就是* 和 * 之前一个字符只匹配s串的当前一个字符就不看 * 号了 即 dp[i][j]=dp[i][j-1]
匹配多个,比如aabb aab* b* 匹配了bb两个b 那么看aab 和aab*是否能匹配上就行了,即dp[i][j]=dp[i-1][j]
(2.2) p[j-2]!=s[i-1] && p[j-2]!=’.’
j-2的字符不等于i-1的字符,那就只能让* 代表取0个字符。
dp[i][j] = dp[i][j-2] (相当于去掉p[j-1]和p[j-2])
3)else(j处就是个普通字符,dp[i][j]肯定不能匹配了,其实这里写不写都可以,只不过为了让大家看着思路清晰。)
dp[i][j] = false;
class Solution {
public:
bool isMatch(const string& s, const string& p)
{
int lens = s.size();
int lenp = p.size();
if (s.size() == 0 && p.size() == 0) return true;
vector<vector<bool>> dp(lens + 1, vector<bool>(lenp + 1, false));
dp[0][0] = true;
//初始化第一行
for (int j = 1; j <= lenp; j++) {
// if (j == 1) dp[0][j] = false; 这里是考虑s为空,p长度为1,这时候肯定不能匹配,其实不判断也可以,因为初始值就是false
//如果p[j-1]为*,那就看p[j-2]是否匹配,如果匹配,那当前j也匹配。
if (p[j - 1] == '*' && dp[0][j - 2]) dp[0][j] = true;
}
for (int i = 1; i <= lens; i++) {
for (int j = 1; j <= lenp; j++) {
if (s[i - 1] == p[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else if (s[i - 1] != p[j - 1]) {
if (p[j - 1] == '.') {
dp[i][j] = dp[i - 1][j - 1];
}
else if (p[j - 1] == '*') {
//p需要能前移1个。(当前p指向的是j-1,前移1位就是j-2,因此为j>=2)
if (j >= 2) {
if (p[j - 2] == s[i - 1] || p[j - 2] == '.') {
dp[i][j] = dp[i][j - 2] || dp[i][j - 1] || dp[i - 1][j];
}
else if (p[j - 2] != s[i - 1] && p[j - 2] != '.') {
dp[i][j] = dp[i][j - 2];
}
}
}
}else {
dp[i][j] = false;
}
}
}
return dp[lens][lenp];
}
};
注意,一定要小心,i和j不要写错了,思考清楚每个变量的含义,不然z找bug找的哭死。
13. 最长递增子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
动态规划思想
dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
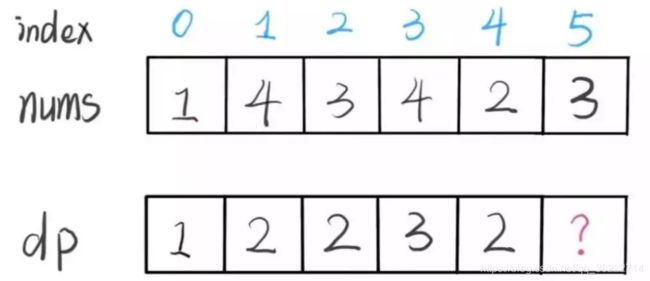
根据刚才我们对 dp 数组的定义,现在想求 dp[5] 的值,也就是想求以 nums[5] 为结尾的最长递增子序列。
nums[5] = 3,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到最后,就可以形成一个新的递增子序列,而且这个新的子序列长度加一。
当然,可能形成很多种新的子序列,但是我们只要最长的,把最长子序列的长度作为 dp[5] 的值即可。
参考
https://mp.weixin.qq.com/s/Ca5hePMiQDX9YwU8TIGQVw
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int len=nums.size();
vector<int> dp(len,1);
for(int i=0;i<len;i++){
for(int j=0;j<i;j++){
if(nums[j]<nums[i]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}
int l=0;
for(int i=0;i<len;i++){
l=max(l,dp[i]);
}
return l;
}
};
二分法思想
先保存数组第一个数,从下标1遍历数组,如果大于那个数就放到后面的堆里面,否则查找应该插入到哪个位置
例如针对上述数列A:5,2,8,6,3,6,9,7,根据算法过程可得:
| 5 | 8 | 6 | 9 | ||
|---|---|---|---|---|---|
| 2 | 6 | 7 | |||
| 3 |
参考
https://blog.csdn.net/sinat_31790817/article/details/78348722
https://mp.weixin.qq.com/s/Ca5hePMiQDX9YwU8TIGQVw
class Solution {
public:
int bserach(vector<int>& dp, int rlen, int target) {
int left = 0, right = rlen - 1;
int mid;
while (left <= right) {
mid = (left + right) / 2;
if (dp[mid] > target) {
right = mid - 1;
}
else if (dp[mid] < target) {
left = mid + 1;
}
else {
return mid;
}
}
return left;
}
int lengthOfLIS(vector<int>& nums) {
int len = nums.size();
if(len==0) return 0;
vector<int> dp(len, 0);
int rlen = 1;
dp[0] = nums[0];
for (int i = 1; i < len; i++) {
if (nums[i] > dp[rlen - 1]) {
rlen++;
dp[rlen - 1] = nums[i];
}
else {
int index = bserach(dp, rlen, nums[i]);
dp[index] = nums[i];
}
}
return rlen;
}
};