NHOI2017初中组解题报告

 

第一题 元音字母(vowel)

【题意分析】

给定一个长度小于等于10⁶且只包含字母的字符串，求元音字母（a,e,i,o,u）的个数。

【解题思路】

对于每一位字符逐一进行判断并统计，但要注意大小写字母的区别。可以统一转换为大写或小写方便判断。

【时空复杂度】

时间复杂度：O(n)

空间复杂度：O(n)

【解题反思】

此题作为比赛的第一题，难度较低，但仍要注意一些细节：

1.          若C++选手使用字符数组，考虑到数据范围较大，必须设为全局变量，否则可能引发运行时错误。

2.       C++中的string是从第0位开始储存的，如果从1开始计算可能导致答案错误。

3.       题目中已经明文提示了，要注意大小写的区别。

【参考程序】

#include

#include

#include

#include

#include

#include

 

using namespace std;

 

const int maxlen = 1e6 + 100;

 

char str[maxlen];

 

int main(void) {

    freopen("vowel.in","r", stdin);

    freopen("vowel.out","w", stdout);

    gets(str);

    int ans =0;

    for (int i= 0; str[i] != '\0'; i++) { //char数组的最后一位为'\0'

        char ch= tolower(str[i]); //统一将当前位转为小写

        ans +=ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u';

    }

    printf("%d\n",ans);

    return 0;

}

第二题 直角坐标系(coordinates)

【题意分析】

给定平面直角坐标系中的n个格点（所有的点两两不同），按一定的原则绘制该坐标系：

1.          整个坐标系分为四个象限，只要该象限或与其相邻的两个象限中同时存在格点，就必须将该象限绘制出来。

2.      格点所在的坐标表示为‘*’

3.      在与原则2不冲突的情况下，x 轴表示为‘|’，y轴表示为‘-’，原点表示为‘+’

【解题思路】

直接按照题意模拟即可，但具体的实现上要注意细节。平面直角坐标系中点坐标的表示法为(x,y)，但输出时是由上至下（y递减）、由左至右（x递增）的，故要进行处理。

首先要确定输出的范围，通过观察样例可以发现，如果记最终输出的坐标系当中x的取值范围为[minx,maxx]，那么就有minx=min{x_i­,0}，maxx=max{x_i,0}，y同理。

之后则以y递减，x递增的顺序打印整个坐标系，判断当前位置是否存在点有两种方法：

一、数组计数法（我在考试时的写法）

考虑到数据范围较小，且不存在重复的点，不妨在输入时用bool数组a[j][i]表示横坐标为j、纵坐标为i的位置是否存在点。但C++中数组下标从0开始，又因为坐标的绝对值不超过100，因此可以统一加上100即可避免出现负数的问题。此方法的编程复杂度较低。

30%的做法：不考虑点坐标的正负性，直接进行标记。

二、   点排序法

可以将输入的点用struct保存（也可用STL中的pair实现）并按输出顺序的优先级排序，在输出时用k表示下一个格点在struct数组中的下标，若p[k].x==j且p[k].y==i则当前位置是格点，输出‘*’后将k累加，指向下一个点。此方法的空间复杂度较低。

需要注意的是，由于枚举每一个位置并判断输出的这一过程是不可能省去的，故时间复杂度不可能比方法一更优。但此方法不必担心坐标的正负性问题，风险较低。

【时空复杂度】

不妨记坐标值的跨度范围为m，点的个数为n（显然0≤n≤m²），有：

数组计数法：

时间复杂度：O(m²)

空间复杂度：O(m²)

点排序法：

时间复杂度：O(m²)

空间复杂度：O(n)

【解题反思】

1. 我在考试时编写的程序没有AC，是因为忽略了在原点位置有一个点的情况。由此可见，对于此类难度不高的模拟题，一定要小心谨慎，“细节决定成败”。

2. 在考试这种限时的场合，在考虑到多种不同的实现方法时，应粗略计算各自的时空复杂度、编程复杂度和期望得分，加以比较后再决定策略，编写程序。

【参考程序】

方法一：

#include

#include

#include

#include

#include

#include

 

usingnamespace std;

 

constint maxp = 1e3; //坐标值的最大跨度，稍微开大一些，空间上不会有问题

 

intn;

boolf[maxp][maxp]; //第一维为横坐标（列），第二维为纵坐标（行）！！

 

intmain(void) {

    freopen("coordinates.in","r", stdin);

    freopen("coordinates.out","w", stdout);

    scanf("%d", &n);

    memset(f, false, sizeof f);

    int minx = 0, miny = 0, maxx = 0, maxy = 0;//必须包含坐标轴，故初始化为0

    for (int i = 0; i < n; i++) {

        intx, y;

        scanf("%d%d", &x, &y);

        minx = min(minx, x); maxx = max(maxx,x);

        miny = min(miny, y); maxy = max(maxy,y);

        f[x+ 100][y + 100] = true; //统一向右上方偏移100位

    }

    for (int i = maxy; i >= miny; i--) { //列递减

        for (int j = minx; j <= maxx; j++) //行递增

            if (!i && !j)putchar(f[100][100] ? '*' : '+'); //原点

            else if (!i && !f[j + 100][i+ 100]) putchar('-'); //x轴

            else if (!j && !f[j + 100][i+ 100]) putchar('|'); //y轴

            else putchar(f[j + 100][i + 100] ?'*' : '.'); //其余点

        putchar('\n');

    }

    return 0;

}

方法二：

#include

#include

#include

#include

#include

#include

 

using namespace std;

 

const int maxn = 250 + 50; //格点的数量

 

typedef pair pii; //用STL自带的pair减少编码量

 

pii points[maxn];

bool cmp(const pii a, constpii b) { //按输出顺序排序，先y递减，再x递增

    return a.second > b.second || !(a.second ^ b.second)&& a.first < b.first;

}

 

int n;

 

int main(void) {

    freopen("coordinates.in", "r", stdin);

    freopen("coordinates.out", "w", stdout);

    scanf("%d", &n);

    int minx = 0, miny = 0, maxx = 0, maxy = 0;

    for (int i = 0; i < n; i++) {

        scanf("%d%d", &points[i].first,&points[i].second);

        minx = min(minx, points[i].first); maxx = max(maxx, points[i].first);

        miny = min(miny, points[i].second); maxy = max(maxy,points[i].second);

    }

    sort(points, points + n, cmp);

    intk = 0;

    for (int i = maxy; i >= miny; i--) {

        for (int j = minx; j <= maxx; j++)

            if (k < n && points[k].first == j &&points[k].second == i) {

                putchar('*'); //是格点

                k++;

            } else putchar(!i ? (!j ? '+' : '-') : (!j ? '|' :'.'));//分类讨论

        putchar('\n');

    }

    return 0;

}

 

第三题 折纸(folding)

【题意分析】

有一张W×H的矩形纸张，要将其折成w×h的矩形纸张，每次折痕要平行于纸张的某一条边。求最少折的次数，若无解则输出-1。

【解题思路】

方法一：

对于20%的子任务，W和w无需考虑，只需对H和h进行分类讨论即可。

期望得分：20分。

方法二：

首先明确一点，如果我们将a视作矩形的长，b视作矩形的宽，那么将a×b的矩形旋转90°之后是等价于b×a的矩形的。于是就可以先把两个矩形统一为a≤b的形式。要满足题目要求，必须保证新矩形能嵌套在原矩形内，如图1所示。

图1 新矩形能嵌套在原矩形内

即，如果此时W<w或H<h，显然无法将矩形的某条边折到比它更长，那么无解；否则总是存在至少一种合法折叠方案。

下面来考虑折纸的过程。不妨设我们现在有一个W×H的矩形，左右折叠一次之后H是不变的，可以得到一个W’×H的矩形，其中

道理不难理解，一次折纸可以使某条边的长度大于等于原来的一半而小于原来的长度（显然若等于原来的长度则没有意义），考虑到题目中边的长度总是正整数，因此下限向上取整。

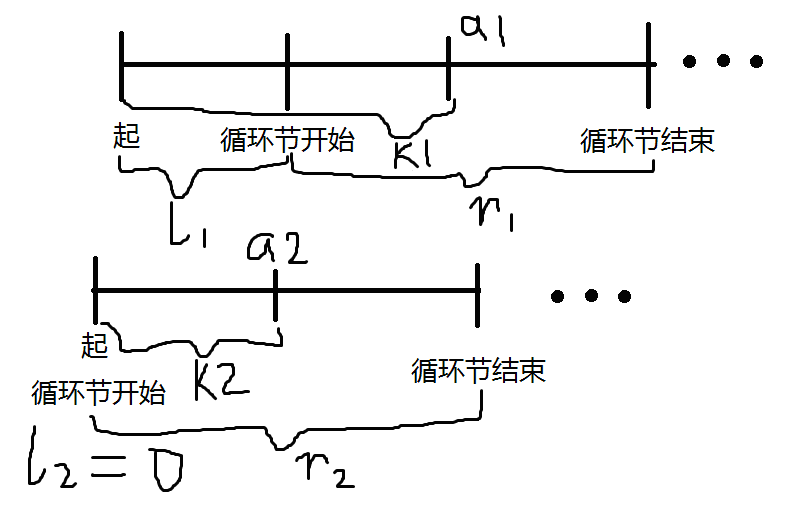
这样一来可以知道，将一条边折成一条更短边的过程，是与另一条边无关的。根据贪心策略，当>a时（即当前边太长了，还不能一次折成目标情况）总是将其折半。因此就可以得到将W折成w和将H折成h所需步数，它们的和即为所求。

但是，这样考虑并不全面。之前为了判断是否非法，我们强制令W<H且w<h。若不非法，则w≤W且h≤H，当然可以将W折成w，H折成h，和图1所示的情况是一致的。

但是，也可以将新矩形旋转90°，考虑将W折成h且将H折成w的情况，如图2所示。

图2 另一种可能

于是在求解时有必要进行分类讨论，看两种解法中哪个更优。

期望得分：100分。

【时空复杂度】

时间复杂度：O(log₂n)

空间复杂度：常数级别

【解题反思】

1.      细节一定要考虑清楚，例如对半折之后应该向上取整的问题，要自己动手试一试。

2.      在解题中初步体会分类讨论的思想，注意分类讨论时既不能遗漏又不能重复。

【参考程序】

#include

#include

#include

#include

#include

#include

 

using namespace std;

 

int W, H;

int w, h;

 

int fold(int from, const int to) { //将长度为from的某条边折成长度为to所需次数

    int cnt;

    for (cnt =0; from > to; cnt++) from = (from + 1 >> 1); //向上取整！！

    return cnt;

}

 

int main(void) {

    freopen("folding.in","r", stdin);

    freopen("folding.out","w", stdout);

    scanf("%d%d",&W, &H); if (W > H) swap(W, H);

    scanf("%d%d",&w, &h); if (w > h) swap(w, h);

    if (W

    else {

        int ans= fold(W, w) + fold(H, h); //考虑第一种情况

        if (W>= h && H >= w) ans = min(ans, fold(W, h) + fold(H, w));//第二种

        printf("%d\n",ans);

    }

    return 0;

}

 

 

第四题 两个数(twonum)

【题意分析】

给定正整数m和小于m的非负整数h₁、a₁、x₁、y₁，h₂、a₂、x₂、y₂（h₁≠a₁,h₂≠a₂），求h₁变成a₁且h₂变成a₂所需的最小用时，其中：

1.       h₁=(x₁×h₁+y₁) modm

2.       h₂=(x₂×h₂+y₂) modm

3.       上述变换总在同时发生，每次耗去1秒。

若无法完成任务，则输出-1。

【解题思路】

首先，将样例推算一下，不难发现h₁和h₂的变换会出现循环，且循环节长度不会超过m。

可以用鸽巢原理证明：考虑可能出现的最坏情况，即使由最初的h₁开始，经过m-1次变换后，h₁被均匀地分布在区间[0,m)当中，每个数正好出现1次。那么在第m次，也一定会变成[0,m)中的某一个数k，此时是它第二次出现。

不妨记上一次出现k的时间为t，则循环节长度为m-t，显然不超过m。

在此基础上，可以令两个数分别以h₁和h₂为初始值，同时代入式子进行变换，于是不难得到它们最早变成a₁和a₂的时刻A₁、A₂以及各自的循环节长度B₁、B₂。具体的方法是：

1.                  记当前时间为tick，每一轮先将tick递增，并将两个数分别代入式子变换；

2.                  对于最早出现的h₁=a₁，令A₁=tick，第二个数同理；

3.                  用rec1[i]记录第一个数变成i的时刻，即：若rec1[h₁]未被赋值，说明它是第一次出现，进行标记rec1[h₁]=tick，否则出现了循环，且tick-rec1[h₁]即为循环节长度。对于最早出现的循环，令B₁=tick-rec1[h₁]。第二个数同理；

4.                  当两个数都找到循环节时，停止。

首先对第3点作一个简要的证明。式子h₁=(x₁*h₁+y₁)mod m中，只有h₁是变值，其它都是常数，即，对于同一个h₁，代入后得到新的h₁仍然是相等的，这是找循环节的依据。

上述过程大体上是正确的，但其实也可以进行一点改动，不妨考虑一种最特殊的情形：在模拟变换的过程中就出现了两者同时满足要求，则tick即为所求，直接退出即可。

在不满足这种条件的情况下，若变换过程中出现了循环，且A₁1]，那么一定不合法。解释一下：根据变换过程第3点，rec[h₁]为起始循环时刻，且[rec[h₁],tick)中的数就是循环节中的数。按照我们的定义，A₁为h₁最早变成a₁的时刻。如果它小于rec[h₁]意味着它只出现一次（或根本不出现）。而两个数又没有在变换过程中同时满足要求，故无解。

此外，当两个数都找到循环节后，如果a₁或a₂没有出现过，也是无解的。

否则，a₁和a₂一定在它们各自的循环节中，大体上表现为图3的形式：

图3 两个数的循环

我们知道，a₁最早出现的时刻为A₁，循环节长度为B₁，那么它下一次出现的时刻为A₁+B₁，再下一次为A₁+2*B₁，……，第x次为A₁+x*B₁。第二个数同理。

考虑到A₁、A₂之间存在差距，而每一个循环节会使它们之间差距得到改变，因此最终会汇集到一起。即，我们总是能够找到一组正整数解(x,y)使得A₁+x*B₁=A₂+y*B₂，而使相等值最小的解即为所求。

考虑到A₁、B₁、A₂和B₂均为常数，不妨将式子变形，得到

这样，我们可以枚举x，从而得到y。最早能够使y为整数的情况即为解。

但还有一种特殊情况需要注意：如果B₁、B₂之间存在倍数关系，而A₁≠A₂，那么无解，如图4。形象化地理解，就是一个人在追另一个人，起点不同，而速度相同，永远追不上。

图5 另一种不合法情况

【时空复杂度】

时间复杂度：近似O(m)

空间复杂度：O(m)

【解题反思】

对于这类涉及的量比较多的题目，只看题来分析是很难有思路的。可以用一些简单的例子入手，尝试找到一些规律，再由特殊情况推广到普遍情况。

另外，实际竞赛中时间比较紧迫。对于没有把握的解法，其实也可以本着“大胆猜想，不用求证”的思想试一试。更保险的方法是用分段算法：在时间条件允许的情况下，针对不同限制的子任务编写不同算法。

【参考程序】

#include

#include

#include

#include

#include

 

using namespace std;

 

const int maxm = 2e6;

 

typedef long long LL;

 

LL m;

LL h1, a1, x1, y1;

LL h2, a2, x2, y2;

int rec1[maxm], rec2[maxm];

 

LL solve() {

       memset(rec1, 0, sizeof rec1); //时间戳

       memset(rec2, 0, sizeof rec2);

       int tick = 0; //时刻

       LL A1 = 0, B1 = 0; //含义如题解所示

       LL A2 = 0, B2 = 0;

      

       while (!B1 || !B2) { //当两个数都找到循环节时才停止

              ++tick;

              h1 = (x1 * h1 + y1) % m;

              h2 = (x2 * h2 + y2) % m;

              if (h1 == a1 && h2 == a2) return tick; //模拟过程中直接就相同了

             

              if (!rec1[h1]) rec1[h1] = tick; //首次出现

              else if (!B1) { //出现循环节

                     B1 = tick - rec1[h1];

                     if (A1 < rec1[h1]) return -1; //要找的数不在循环节中

              }

              if (h1 == a1 && !A1) A1 = tick; //要找的数首次出现

             

              //同理

              if (!rec2[h2]) rec2[h2] = tick;

              else if (!B2) {

                     B2 = tick - rec2[h2];

                     if (A2 < rec2[h2]) return -1;

              }

              if (h2 == a2 && !A2) A2 = tick;

       }

      

       if (!A1 || !A2 || !(B1 % B2) || !(B2 % B1)) return -1; //考虑一些不合法情况

      

       LL diff = A1 - A2; //定值提取出来，避免重复计算，优化常数

       for (LL i = 0; ; i++) {

              if ((B1 * i + diff > 0) && !((B1 * i + diff)% B2)) return A1 + B1 * i;

       }

}

 

int main(void) {

       freopen("twonum.in", "r", stdin);

       freopen("twonum.out", "w", stdout);

       int T;scanf("%d", &T);

       while (T--) {

              scanf("%lld", &m);

              scanf("%lld%lld%lld%lld", &h1, &a1,&x1, &y1);

              scanf("%lld%lld%lld%lld", &h2, &a2,&x2, &y2);

              printf("%lld\n", solve());

       }

       return 0;

}

 

 

第五题 取值(numbers)

【题意分析】

给定正整数n,m（其中n≤m），要求找到一个单调不下降的非负整数序列x₁,x₂,…,x_n使得∑x_i=m，求方案总数除以10⁸+7的余数。

【解题思路】

只要对题目稍加分析，不难发现这其实就是经典的完全背包问题：在[1,m]范围内选取n个允许出现重复的正整数，使它们的和为m。

但考虑到所选数必须递增的限制，不妨定义f[i][j][k]为选取i个不大于j的正整数，使它们的总和为k的方案总数。所求即为，转移方程也比较好推：

这里要解释一下，j’的取值问题。易知它不能超过j，但同时也要注意不能超过k，否则所选的数比总和还要大，显然是不合理的。边界条件就是i=1时，若k<=j则值为1。

直接根据这个式子进行转移是会超时的，因此可以改写为记忆化搜索的形式，就可以通过了。

【时空复杂度】

时间复杂度：理论上限O(T*n*m²)，但记忆化会有一定优化，实际上达不到这个复杂度

空间复杂度：O(n*m²)

【解题反思】

有很多考题其实是从我们平时训练的经典题目进行变式的，只有留心观察，善于总结，才能迅速找到题目中蕴含的模型，从而找到解决的方法。

【参考程序】

#include

#include

#include

#include

#include

#include

 

using namespace std;

 

const int mod = 1e8 + 7;

const int maxn = 302;

 

int f[maxn][maxn][maxn];

int t[maxn][maxn][maxn]; //标记是否被计算过，巧妙地利用数据组数省去memset耗时

int T;

 

int solve(int cnt, int last,int sum) {

       if (t[cnt][last][sum] == T) return f[cnt][last][sum];

       t[cnt][last][sum]= T;

       int &ret =f[cnt][last][sum];

       if (cnt == 1) return ret = sum <= last;

       ret = 0;

       int to = min(last, sum);

       for (int i = 0; i <= to; i++)

              (ret += solve(cnt - 1, i, sum - i)) %= mod;

       return ret;

}

 

int main(void) {

       freopen("numbers.in", "r", stdin);

       freopen("numbers.out", "w", stdout);

       scanf("%d", &T);

       while (T) {

              int m, n; scanf("%d%d", &m, &n);

              if (n == 1) puts("1"); //注意边界值的考虑

              else {

                     int ans = 0;

                     for (int i = 0; i <= m; i++)

                            (ans += solve(n - 1, i, m - i)) %= mod;

                     printf("%d\n", ans);

              }

              --T;

       }

       return 0;

}

 

 

第六题 数对(pairs)

【题意分析】

给定正整数n，要求构造有序整数对序列(a₁,b₁),(a₂,b₂),(a₃,b₃),…,(a_m,b_m)满足：

1.       1≤a_i≤n，|b_i|≤n，a_i≠|b_i|；

2.       不存在重复的数对；

3.       对于b_i>0的数对，必须存在数对(a_j,b_j)满足jj=b_i且b_j=0；

4.       对于b_i<0的数对，不能存在数对(a_j,b_j)满足jj=|b_i|且b_j=0；

5.       对于所有ii和b_i+1的正负性不相同。

求合法情况下能构造出最大的m值。

【解题思路】

看到题目的限制比较多，一下子都考虑上是不太实际的，不如分步解决。

首先考虑1和2，a有n种取值，对于每一个a，有2n-1种b（考虑到它的绝对值不能等于a），又因为不存在重复的数对，因此总共可以构造出n*(2n-1)种数对。或者说，对于每一个b，有n-1种a，总共可以构造出(2n+1)*(n-1)+1种（b=0时有n种a），也一样。

最理想的状态，当然是能够找到一种排列，使得它们正好全部都能被用上，那么答案自然就是n*(2n-1)。（但是实际上是无法达到的。）

我们再来考虑5，相邻两个数对中b的正负性不能相同，容易想到一种策略：把(1,0),(2,0),(3,0),...,(n,0)先放好（事实上，打乱顺序一样可以得到最后的结论，但是相比之下按顺序放会更容易理解一些），再在它们之间让b正负交替地插入数对。

现在只剩下限制3和4。所有b_i>0的数对(a_i,b_i)必须被放在(b_i,0)的后面。而b_i<0的数对则必须被放在(|b_i|,0)的前面。既然我们的(1,0),(2,0)...是从大到小排列的，也就意味着，在(1,0)和(2,0)之间，b如果要取正数，一定只能取1，这绝对是确凿无疑的。

而如果b要取负数，则不能取-1，那还剩下-2到-n，不妨只考虑取-2。因为(1,0)和(2,0)之间相邻数对的b要正负交替，因此b取一个正数、一个负数进行配对就刚刚好。而且，所有合法的(x,1)和(x,-2)都可以被插入到(1,0)和(2,0)之间。

同理，在(2,0)和(3,0)之间可以插入(x,2)和(x,-3)……之后不断依此类推，最后我们发现b会剩下n和-1没有被取过。此时，我们如果要放(x,n)，必须放在(n,0)后面。放完之后，后面无法再接任何数对了。（如果要接(y,n)，正负性相同，产生冲突；如果要接(z,-1)，它前面出现了(1,0)，不合法）同样的，我们只能在(1,0)前面放一个(x,-1)。

这样，跟-1和n配对的a就只有1个，比我们最初推算出来的：对于每一个b，有n-1种a的结论少了n-2个，因此总方案数要减去2*(n-2)，即，最终的答案为n*(2n-1)-2*(n-2)，化简后为2*n²-3n+4。题目的数据范围较大，注意要开long long类型。

【时空复杂度】

时间复杂度：O(1)

空间复杂度：O(1)

【解题反思】

对于限制条件比较多的题目，不能“一口吃成胖子”，而是要采用逐步考虑和分析的方法。这样一来，即便是许多看起来比较复杂的题目，最终的结论也许会出人意料的简单。

【参考程序】

#include

#include

#include

#include

 

using namespace std;

 

int main(void) {

       freopen("pairs.in", "r", stdin);

       freopen("pairs.out", "w", stdout);

       long long n;

       scanf("%lld", &n);

       printf("%lld\n", n == 1 ? 1 : (n * n << 1) - 3* n + 4); //注意n=1的情况

       return 0;

}