kaggle波士顿房价预测
一.项目背景
比赛总的情况是给你79个特征然后根据这些特征预测房价(SalePrice),其中既有离散型也有连续性特征,而且存在大量缺失值。在data_description.txt这个文件,里面对各个特征的含义进行了描述,便于对缺失值进行插补。
这个比赛的评价指标的均方根误差(RMSE),这是常用于回归问题的指标。
目前最好的得分如下:

对于新手结果还可以,后续还有很多可优化的空间
二.探索性的可视化
导入数据,查看数据的统计性描述和数据的类型等
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
train_data=pd.read_csv("E:/house price/train.csv")
train_data.info()
train_data.describe()
test_data=pd.read_csv("E:/house price/test.csv")
test_data.info()
test_data.describe()
数据较多,截取部分数据


数据有81列,包含的住宅类型,地理位置等等各个方面的信息
查看训练数据集中各个数据的相关系数,同时目标为SalePrice,需要观察与SalePrice相关性高的特征,这里选择相关系数前10的变量
fig = plt.figure(figsize=(8,8))
corr=train_data.corr()
ax=sns.heatmap(corr,vmax=1,square=True)
bottom,top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
plt.show()
corrprice= corr.nlargest(10,'SalePrice').index
new_data=train_data[corrprice].corr()
fig=plt.figure(figsize=(8,8))
ax=sns.heatmap(new_data,annot=True,square=True,fmt='.2f')
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
plt.show()
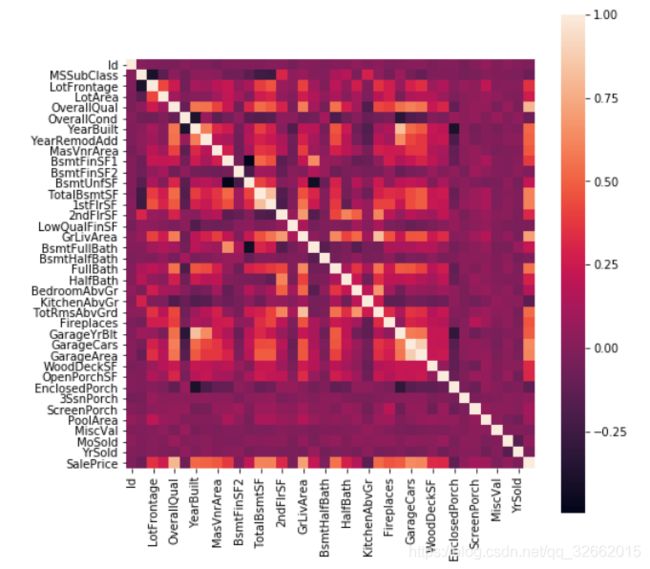
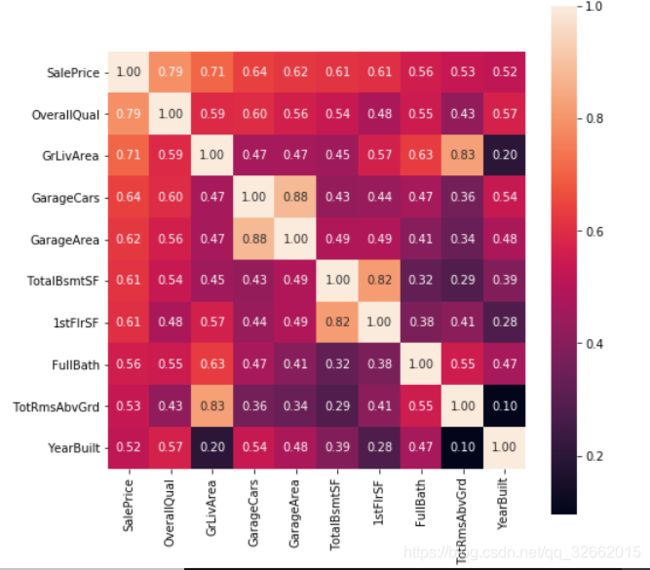
可以看出与SalePrice相关性系数高的变量分别为:房屋的整体评分,地上面积,车库容量,车库面积,地下室总面积,一楼平方英尺,完整浴室,地上房间总数,建造年份。可视化观察特征与SalePrice的关系。
三. 数据的清洗
3.1异常值
sns.pairplot(train_data[corrprice])
plt.show()
sns.pairplot(x_vars=['OverallQual','GrLivArea','TotalBsmtSF','YearBuilt'],y_vars='SalePrice',data=train_data,height=4)
plt.show()
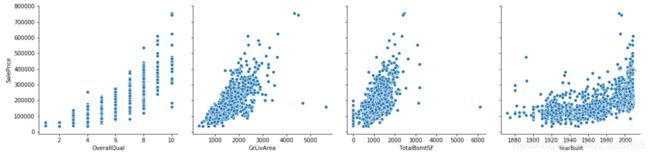
观察结果’OverallQual’,‘GrLivArea’,‘TotalBsmtSF’,'YearBuilt’四个特征中存在异常值,考虑到这些特征对SalePrice的影响,需要将异常值去除,同时需要重置索引值,使得索引值连续
train_data.drop(train_data[(train_data.GrLivArea>4000)&(train_data.SalePrice<200000)].index,inplace=True)
train_data.drop(train_data[(train_data.OverallQual<5)&(train_data.SalePrice>200000)].index,inplace=True)
train_data.drop(train_data[(train_data.YearBuilt<1900)&(train_data.SalePrice>400000)].index,inplace=True)
train_data.drop(train_data[(train_data.YearBuilt>1980)&(train_data.SalePrice>700000)].index,inplace=True)
train_data.drop(train_data[(train_data.TotalBsmtSF>6000)&(train_data.SalePrice<200000)].index,inplace=True)
train_data.reset_index(drop=True,inplace=True)
train_data.shape
from scipy.stats import norm
(mu,sigma) =norm.fit(train_data.SalePrice)
fig = plt.figure(figsize=(8,8))
sns.distplot(train_data.SalePrice,fit=norm)
plt.ylabel('Frequency')
plt.legend(['u={:.2f} and sigma={:.2f}'.format(mu,sigma)],loc='best')
plt.show()
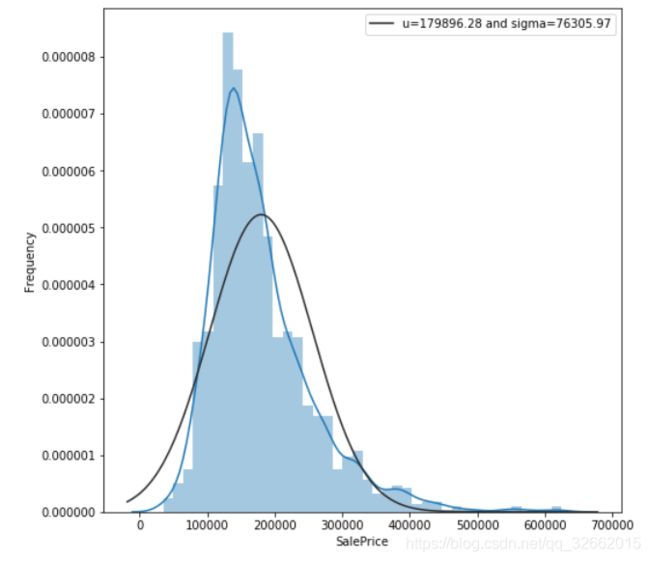
此时的拟合正太曲线的均值179896.28,标准差76305.97,对于偏态分布的数据,将其用log函数转化为正态分布。其目的(1)变换后可以更便捷发现数据的关系 (2)数据有偏,可以拉开数据差异 (3)数据模型符合理论模型的假设,取对数后性质和相关关系不会改变,但压缩了尺度,方便计算
train_data.SalePrice =np.log1p(train_data.SalePrice)
(mu,sigma) =norm.fit(train_data.SalePrice)
fig = plt.figure(figsize=(8,8))
sns.distplot(train_data.SalePrice,fit=norm)
plt.ylabel('Frequency')
plt.legend(['u={:.2f} and sigma={:.2f}'.format(mu,sigma)],loc='best')
plt.show()
3.3 训练和测试数据集的合并
主要是为了便于数据的清洗以及特征过程
all_data=pd.concat([train_data,test_data],axis=0,ignore_index=True,sort=False)
all_data.shape
all_data.info()
all_data.describe()
![]()
3.4缺失值的处理
将所有的缺失值列出来
miss_data= all_data.isnull().sum().sort_values(ascending =False)
ratio = (miss_data/len(all_data)).sort_values(ascending=False)
missing_df = pd.concat([miss_data,ratio],axis=1,keys=['miss_data','ratio'],sort=False)
missing_df[missing_df>0].count()
missing_df[:35]

缺失值的处理原则:
1.如果缺失值比例过大,建议直接删除
2.用均值,中值,众数等进行填充
3.用拟合的方法:要求变量与缺失变量有关
4.映射到更高维空间。如男,女,缺失。映射成是否男,是否女,是否缺失
这里缺失值处理也按照1-4原则,同时根据data_description的描述进行数据填充。具体处理如下:
没有的属性用None的填充
all_data.PoolQC=all_data.PoolQC.fillna('None')
all_data.MiscFeature=all_data.MiscFeature.fillna('None')
all_data.Alley=all_data.Alley.fillna('None')
all_data.Fence=all_data.Fence.fillna('None')
all_data.FireplaceQu=all_data.FireplaceQu.fillna('None')
all_data.GarageFinish=all_data.GarageFinish.fillna('None')
all_data.GarageCond=all_data.GarageCond.fillna('None')
all_data.GarageQual=all_data.GarageQual.fillna('None')
all_data.GarageType=all_data.GarageType.fillna('None')
all_data.BsmtExposure=all_data.BsmtExposure.fillna('None')
all_data.BsmtCond=all_data.BsmtCond.fillna('None')
all_data.BsmtQual=all_data.BsmtQual.fillna('None')
all_data.BsmtFinType1=all_data.BsmtFinType1.fillna('None')
all_data.BsmtFinType2=all_data.BsmtFinType2.fillna('None')
all_data.MasVnrType =all_data.MasVnrType.fillna('None')
数值型的缺失,用0填充
all_data.GarageCars=all_data.GarageCars.fillna(0)
all_data.GarageYrBlt=all_data.GarageYrBlt.fillna(0)
all_data.GarageArea=all_data.GarageArea.fillna(0)
all_data.BsmtFullBath=all_data.BsmtFullBath.fillna(0)
all_data.BsmtHalfBath=all_data.BsmtHalfBath.fillna(0)
all_data.BsmtFinSF1=all_data.BsmtFinSF1.fillna(0)
all_data.BsmtFinSF2=all_data.BsmtFinSF2.fillna(0)
all_data.BsmtUnfSF=all_data.BsmtUnfSF.fillna(0)
all_data.TotalBsmtSF=all_data.TotalBsmtSF.fillna(0)
all_data.MasVnrArea= all_data.MasVnrArea.fillna(0)
用众数填充:
all_data.SaleType=all_data.SaleType.fillna(all_data.SaleType.mode()[0])
all_data.Exterior1st=all_data.Exterior1st.fillna(all_data.Exterior1st.mode()[0])
all_data.Electrical=all_data.Electrical.fillna(all_data.Electrical.mode()[0])
all_data.Exterior2nd=all_data.Exterior2nd.fillna(all_data.Exterior2nd.mode()[0])
all_data.KitchenQual=all_data.KitchenQual.fillna(all_data.KitchenQual.mode()[0])
all_data.MSZoning=all_data.MSZoning.fillna(all_data.MSZoning.mode()[0])
Functional缺失值意味着典型
all_data.Functional=all_data.Functional.fillna(‘Typ’)
LotFrontage 街区面积属性。位于同一街道的房屋往往有相同的街区属性。因此利用不同的街道分组,再用均值填充
all_data['LotFrontage']=all_data.groupby('Neighborhood')['LotFrontage'].apply(lambda x:x.fillna(x.median()))
查看数据是否还存在缺失值
miss_data= all_data.isnull().sum().sort_values(ascending =False)
ratio = (miss_data/len(all_data)).sort_values(ascending=False)
missing_df = pd.concat([miss_data,ratio],axis=1,keys=['miss_data','ratio'],sort=False)
missing_df[:2]

需要将Id和SalePrice这两列数值去除,这样数据清洗基本完成
all_data.drop(['Id','SalePrice'],axis=1,inplace=True)
四.特征工程
4.1数值型转化为字符型
一些特征被表示成数值特征缺乏意义,主要是年份,类别
column1 = ['MSSubClass', 'YrSold','MoSold', 'OverallCond', "BsmtFullBath", "BsmtHalfBath", "HalfBath",
"YearBuilt","YearRemodAdd", "GarageYrBlt"]
for coln in column1:
all_data[coln]=all_data[coln].astype(str)
del coln,column1
4.2 数值特征中存在一些顺序变量,不同于一般的类型变量,顺序变量之间存在固有的顺序,如高低,病人的疼痛等级。顺序变量,标签编码的方式无法正确识别这种顺序关系。
def custom_coding(x):
if(x=='Ex'):
r = 0
elif(x=='Gd'):
r = 1
elif(x=='TA'):
r = 2
elif(x=='Fa'):
r = 3
elif(x=='None'):
r = 4
else:
r = 5
return r
cols1 = ['BsmtCond','BsmtQual','ExterCond','ExterQual','FireplaceQu','GarageCond','GarageQual','HeatingQC','KitchenQual','PoolQC']
for col in cols1:
all_data[col] = all_data[col].apply(custom_coding)
del col,cols1
4.3 字符型特征标签编码,除了之前的顺序编码,其他字符特征进行数值编码,两种方式 one-hot和label_encoder来进行
对年份进行Labelencoder编码,是由于年份的取值过多,直接独热编码会造成数据过于稀疏,严重增加特征维度,因此用labelencoder
from sklearn.preprocessing import LabelEncoder
Labels=['YearBuilt','YearRemodAdd','GarageYrBlt',"YrSold", 'MoSold']
label_encoder =LabelEncoder()
for i in Labels:
label_encoder.fit(all_data[i].values)
all_data[i]=label_encoder.transform(all_data[i].values)
del i,Labels
4.4 构建其他特征
all_data['TotalArea']=all_data['TotalBsmtSF']+all_data['1stFlrSF']+all_data['2ndFlrSF']
all_data['YearofRemodel']=all_data['YrSold'].astype(int)- all_data['YearRemodAdd'].astype(int)
这里只构建了两个特征,一个总面积,这个对房价有大影响,另一个出售日期与翻新的日期间隔,日期越短,房价应该越高,也可以构建其他特征指标
4.5 数值型特征–偏度
为什么要做偏度处理,上面已经解释过了,数据转换的方式,通常是取对数
all_data_nums=all_data.select_dtypes(exclude='object')
all_data_skews= all_data_nums.skew().sort_values()
skews = pd.DataFrame({"skew":all_data_skews})
part_skews=skews[abs(skews)>0.75].dropna()
print("The numbers of skews need to transform is :{}".format(part_skews.shape))
part_skews
from scipy.special import boxcox1p,inv_boxcox1p
for i in part_skews.index:
all_data[i]=boxcox1p(all_data[i],0)
del i
4.6 字符型变量的独热编码
all_data.shape
all_data = pd.get_dummies(all_data,drop_first=True)
all_data.head()
all_data.info()

至此,所有的字符型特征变量都编码成数值型特征
4.7 数据的归一化
先将处理完的数据分成训练和测试
train_data_new=all_data[:len(train_data)]
test_data_new=all_data[len(train_data):]
X=train_data_new
y=train_data.SalePrice
然后将数据进行归一化处理
rs =RobustScaler()
rs.fit(X)
X_rs =rs.transform(X)
X_rs_prd =rs.transform(test_data_new)
为甚么用RobustScaler。删除中位数,并根据百分位数范围(默认IQR:四分位间隔)缩放数据
a‘= (a-center)/scale’,如果你的数据包含许多异常值,使用均值和方差缩放可能并不是一个很好的选择,这种情况下,你可以使用、 RobustScaler 作为替代品。它们对你的数据的中心和范围使用更有鲁棒性的估计
五:数据建模
from sklearn.linear_model import Ridge,Lasso,ElasticNet
from sklearn.decomposition import PCA
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split,KFold
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import GridSearchCV,cross_val_score
from sklearn.preprocessing import RobustScaler
初步准备使用Lasso,Ridge, ElasticNet,SVR这几个模型,在应用模型之前,需要先将评价标准定义
def rmsle(model,X,y):
return np.sqrt(-cross_val_score(model,X_rs,y,scoring='neg_mean_squared_error',cv=kfold))
5.1Lasso 模型
lasso=Lasso(random_state=0)
las_param={'alpha':[0.0001,0.0002,0.0003,0.0004,0.0006,0.0007],
'max_iter':[10000]}
las_gcv=GridSearchCV(lasso,las_param,cv=kfold,scoring='neg_mean_squared_error',verbose=1,n_jobs=3)
las_gcv.fit(X_rs,y)
best_lasso=las_gcv.best_estimator_
print('lasso_score:%.4f'%(np.sqrt(-las_gcv.best_score_)))
![]()
这里用网格搜索alpha最佳参数,最终的结果0.1116
5.2Ridge回归
ridge = Ridge(random_state=0)
rid_param ={'alpha':np.arange(1,100,2),
'max_iter':[10000]}
rid_grid=GridSearchCV(ridge,rid_param,scoring='neg_mean_squared_error',cv=kfold,verbose=1,n_jobs=3)
rid_grid.fit(X_rs,y)
best_ridge =rid_grid.best_estimator_
print('lasso_score:%.4f'%np.sqrt(-rid_grid.best_score_))
![]()
5.3ElasticNet
ela_net = ElasticNet(random_state=0)
ela_param={'alpha':[0.002,0.003,0.004,0.006,0.007,0.008],
'l1_ratio':[0.01,0.02,0.03,0.04,0.05],
'max_iter':[10000]}
ela_grid=GridSearchCV(ela_net,ela_param,cv=kfold,scoring='neg_mean_squared_error',n_jobs=3,verbose=1)
ela_grid.fit(X_rs,y)
best_ela=ela_grid.best_estimator_
print('ela_score:%.4f'%np.sqrt(-ela_grid.best_score_))
![]()
5.4Svr
svr=SVR()
svr_param={'gamma':[0.0004,0.0005,0.0006,0.0007],
'kernel':['rbf'],
'C':[12,13,14,15],
'epsilon':[0.006,0.007,0.008,0.009,0.01,0.02]
}
svr_grid=GridSearchCV(svr,svr_param,cv=kfold,n_jobs=3,verbose=1,scoring='neg_mean_squared_error')
svr_grid.fit(X_rs,y)
best_svr=svr_grid.best_estimator_
print('svr_score:%.4f'%np.sqrt(-svr_grid.best_score_))
![]()
5.5 集成模型
5.5.1 blending
from sklearn.model_selection import KFold
from sklearn.base import clone,BaseEstimator
import numpy as np
class StackingAveragedModels(BaseEstimator):
def __init__(self,base_models,meta_model,n_folds=5):
self.base_models = base_models
self.meta_model = meta_model
self.n_folds = n_folds
def fit(self,X,y):
self.base_models_ = [list() for x in self.base_models]
kfold = KFold(n_splits=self.n_folds,shuffle=True,random_state=0)
out_of_fold_predictions = np.zeros((X.shape[0],len(self.base_models)))
for i,model in enumerate(self.base_models):
for train_index,holdout_index in kfold.split(X,y):
instance = clone(model)
instance.fit(X[train_index],y[train_index])
self.base_models_[i].append(instance)
y_pred = instance.predict(X[holdout_index])
out_of_fold_predictions[holdout_index,i] = y_pred
self.meta_model.fit(out_of_fold_predictions,y)
return self
def predict(self,X):
meta_features= np.column_stack([np.column_stack([model.predict(X) for model in single_model]).mean(axis=1) for single_model in self.base_models_])
return self.meta_model.predict(meta_features)
weight_avg = AverageWeight(mod=[best_lasso,best_ela,best_ridge,best_svr],weight=[0.25,0.25,0.25,0.25])
weight_avg.fit(X_rs,y)
print('weight_score:%.4f'%np.mean(rmsle(weight_avg,X_rs,y)))
![]()
这里用了四个模型混合,由于之前单个模型的得分相差不大,因此给与一样的比例,可以看出RMSE比单个模型有所下降
5.5.2 stacking
具体原理如下图所示:

简单来说就是第一层的每个模型预测其中一部分数据的结果,假设第一层有4个模型,训练数据集的X 为 MxN ,Y为Mx1
第一次训练后的4个Y_Predict 组成 Mx4的第二层的X,与
Y来训练第二层的模型。类似神经网络
from sklearn.model_selection import KFold
from sklearn.base import clone,BaseEstimator
import numpy as np
class StackingAveragedModels(BaseEstimator):
def __init__(self,base_models,meta_model,n_folds=5):
self.base_models = base_models
self.meta_model = meta_model
self.n_folds = n_folds
def fit(self,X,y):
self.base_models_ = [list() for x in self.base_models]
kfold = KFold(n_splits=self.n_folds,shuffle=True,random_state=0)
out_of_fold_predictions = np.zeros((X.shape[0],len(self.base_models)))
for i,model in enumerate(self.base_models):
for train_index,holdout_index in kfold.split(X,y):
instance = clone(model)
instance.fit(X[train_index],y[train_index])
self.base_models_[i].append(instance)
y_pred = instance.predict(X[holdout_index])
out_of_fold_predictions[holdout_index,i] = y_pred
self.meta_model.fit(out_of_fold_predictions,y)
return self
def predict(self,X):
meta_features= np.column_stack([np.column_stack([model.predict(X) for model in single_model]).mean(axis=1) for single_model in self.base_models_])
return self.meta_model.predict(meta_features)
stack = StackingAveragedModels([best_ela,best_ridge,best_svr],best_lasso)
stack.fit(X_rs,y.values)
print('stack_score:%.4f'%np.mean(rmsle(stack,X_rs,y.values)))

结果有微小提升。将结果导出,导出之前需要将数据用
inv_boxcox1p进行还原
```python
result2 = pd.DataFrame({'Id':test_data['Id'],'SalePrice':y_predict2})
result2.to_csv('E:/house price/result2.csv',index=False)
六.总结
可优化的部分还有很多,如建立更多的特征,在数据建模之前运用PCA,消除特征之间的相关性,另外stacking也不是最终形式,后面再尝试优化

