基于 ODR 和 BSMOTE 的不均衡 SVM 分类算法

---

概述

支持向量机已经成功的应用在许多大规模样本集分类中，但是在这些样本集中可能存在着大量的噪声和冗余信息，进而导致分类器的分类精度不高。因此近年来，大量的去噪声和删减样本的文章不断涌现出。其中欠抽样算法就是通过删减多数类样本的数目以达到均衡样本集的目的。

然而常用的欠抽样方法都是些随机欠抽样方法，这种方法存在着一些缺陷：采样具有很大的随机性，这是由于随机欠抽样方法未考虑样本的分布情况，可能会删除某些重要的多数类样本信息。

针对这一不足，本章将给出一种新的逐级优化递减的欠抽样方法（optiization of decreasing reduction ODR），并给出了一种基于 ODR 和 BSMOTE 算法结合的不均衡数据 SVM 分类算法。在介绍 ODR 算法之前，我们首先介绍一下 KNN 算法。

---

KNN 算法

KNN 算法也叫 K 最近邻（K-Nearest Neighbor, KNN）分类算法，该算法是一种理论上比较成熟的分类算法，也是最简单的分类算法之一。

对于二分类问题，设样本集 (x1,x2,...,xn) 中有 n 个样本，其中样本类别为 {y1,y2} 。对于一个待识别的样本 x，分别计算它和各个已知类别的训练样本之间的距离：

dj(x)=∥∥xj−x∥∥,j=1,2,...,n

选择距离 x 最近的 k 个样本（即 k 个最近邻样本），在这 k 个最近邻样本中哪一类样本最多，就认为 x 是属于哪一类的。

设 k1,k2 分别是待识别样本 x 的 k 个最近邻样本中属于类别 1 和 类别2 的样本数目。则 k1+k2=k 。 定义判别函数是：

di(x)=k，i=1,2

其中 i 是样本的类别，则判决规则是：

dm=max[di(x)]，i=1,2

则识别为 x∈m 类。这种方法就是 k-近邻法，也就是 KNN 法。

---

当 k =1 时，通常也称为最近邻法或者 1-NN 法。当然为了克服个别样本类别的偶然性，增加算法分类的可靠性，通常 k 的值都是大于 1 的奇数。

• 优势：由于 KNN 算法主要是依靠周围有限的最近邻的样本，而不是根据判别类域的方法来判别所属类别的，所以对于类域的重叠或者交叉严重的待识别样本集来说，KNN 方法比其他方法更加合适。
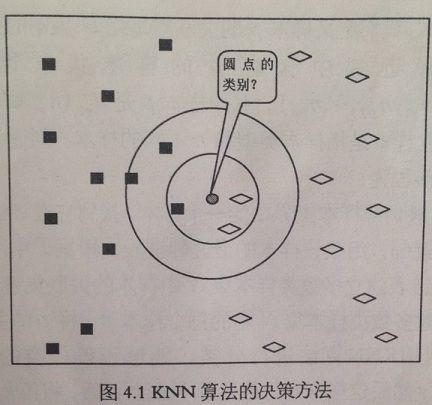
• 缺陷：当样本不均衡时，如一个类别的训练样本数目很大，而另一类别的训练样本数目很小时，则很有可能会导致当输入一个新样本时，该样本的 k 个最近邻中多数类的训练样本占多数。

如上图，当 k=3 和 k=5 时，判别的结果不一致。

---

ODR 欠抽样算法

由于在多数类样本中存在噪声样本和大量的重复信息，这些冗余信息将严重影响 SVM 分类器的界面生成，因此如何提出这些冗余样本而保留有效信息就变得十分重要。传统的欠抽样算法只随机选取多数类的一个自己，没有能考虑采样后子集的信息是否有效。

为了实现对多数类样本集合有目的地筛选，在 KNN 算法的基础上利用多数类样本对领域样本的影响，来对欠抽一样算法进行改进，提出一种新的逐级优化递减欠抽样算法。

---

ODR 核心思想

该算法通过 KNN 算法评价多数类样本对领域内的样本分类影响的好坏程度，依次删除对分类效果有负面影响或影响不大的样本，通过删除多数类中的冗余样本来达到使样本均衡的目的。

---

ODR 具体算法描述

• 设训练样本集为 T，其中多数类样本集是 N，p 是 N 集中的样本

• 我们定义样本 p 的关联集是指 N 集中的其他样本的 k 个最近邻中含有 p 的样本集，即关联集
  Ap={np1,np2,...,npm} ，其中样本 p 是 npi(npi∈Ap) 的最近邻。

• 对立样本是指样本类型和 p 不同的样本。

则逐级优化递减算法的流程为：
1. 对训练样本集 T 中的一个样本，找到它在训练集 T 中的 k 个最近邻，组成该样本的最近邻链表，根据 T 中所有样本的最近邻链表建立多数类样本集 N 中样本的关联集链表

1. 对多数类样本集 N 中的每个样本 p ，将 p 的关联集中的样本利用 KNN 算法进行分类，能够正确分类的个数记为 withp ；然后这些样本的最近邻中去除 p 后，将第 k+1 个最近邻加入，计算此时利用 KNN 算法能够被正确分类的个数，记为 withoutp。

2. 比较 withp 和 withoutp 的值，如果 withp 小于等于 withoutp，则认为删除样本 p 对训练样本集 T 分类的影响比较小。反之，如果 withp 大于 withoutp 时，认为样本 p 对分类器影响比较大。

3. 计算 N 中所有样本在训练样本集 T 中的最近的对立样本。并求出两者之间的欧式距离 dp′

4. 我们可以根据 withp - withoutp 的值从大到小（只在 withp - withoutp >= 0 的情况下），如果 withp - withoutp 的值相同，则按 dp′ 从小到大的顺序优化排列，然后依次递减删除多数类样本，直到多数类数目递减到制定的数目时，算法结束

整体的流程图如下

算法中当 withp -withoutp 的值为负时，即可认为样本 p 的存在对分类器的分类产生了不良影响，则此时我们认为样本 p 是噪声样本；

当 withp -withoutp 的值为 0时，此时在样本 p 周围都是多数类样本，删除样本 p 对分类器的对其它样本的分类影响不大，则认为样本 p 为安全样本（离分类器边界比较远的样本）；

反之，当 withp -withoutp 的值大于 0 时，则此时样本 p 的存在有利于分类器对其它样本的分类，而这些样本大多数是在分类边界附近，所以此时，我们认为样本 p 是边界样本。

在上面的算法实现过冲中可以看出：ODR 算法能够去除多数类样本中噪声样本和安全样本，保留多数类样本的边界样本，能够减少欠抽样时所去除的有用信息，这样能够给更加有利于后续 SVM 分类器的分类性能。

---

ODR-BSMOTE-SVM 算法

虽然过抽样和欠抽样算法都能够达到使训练样本集均衡的目的，但是保存下来的训练样本信息对决策界面的生成不一定有效，因此单纯的将它们与 SVM 相结合并不能从根本上改善 SVM 算法对少数类样本的分类性能。

因此，我们想到将上述两种抽样方法相结合实现数据均衡，并给出一种基于逐级优化递减算法（ODR）和 BSMOTE 算法相结合的 SVM 算法（ODR-BSMOTE-SVM）。该算法既能去除多数类样本的噪声和重复信息，提高数据的利用率，又能在只增加少数类中有效位置样本信息，保留多数类样本有用信息的情况下，实现样本均衡的目的。

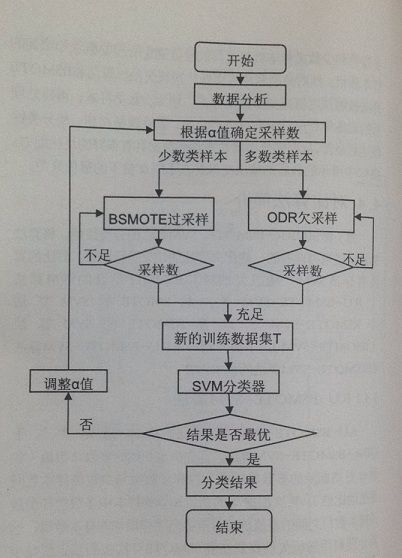
算法的流程图如下所示

从图中可以得知该算法的基本思想是：
1. 首选设参数 α 表示为需要删除的多数类样本个数和多数类与少数类样本数间差值的比值
2. 其次根据 α 的初值和训练样本中多数类和少数类样本数目之间的差值确定所需要删除和增加的样本数目
3. 然后分别利用逐级优化递减欠抽样算法和 BSMOTE 算法按照预定值减少多数类样本，增加少数类样本
4. 再讲处理后的训练集利用 SVM 算法进行分类
5. 最后调整 α 值，使分类性能达到最佳，从而使得分类器对不均衡数据具有很好的泛化能力

---

不同比例下不均衡数据的性能比较

为了测试 ODR-BSMOTE-SVM 算法的泛化能力，也就是测试算法在不同比例下不均衡数据集中的性能，我们选择UCI 数据库中的 Page Blocks Classification 数据集作为测试数据。Page Blocks Classification 数据集含有样本总数 5473，样本属性数目为 9，样本类别数目为 5，其中类别 1 样本有 4913 个，类别 2 样本数目为 329 个，类别 3 样本数目为 28 个，类别 4 样本数目为 88 个，类别 5 样本数目为 115 个，并且选择类别 1 的样本作为所属类赝本，类别 2 的样本作为少数类样本。

1. 选取 50 个少数类样本数，保持少数类样本数目不变的情况下，将两类测试数据的个数按照 5：1，10：1，15：1，20：1，25：1，30：1，35：1，40：1 的比例进行选取

2. 然后利用十折交叉验证的方法进行实验，将测试结果和 BSMOTE-SVM、RU-BSMOTE-SVM、KSMOTE-SVM 算法的结果进行比较

3. 其中 ODR-BSMOTE-SVM 、BSMOTE、KSMOTE 算法中的 k 的值选择为 5，BSMOTE 的算法中 S值为 3，初始 α 值为 0.2。

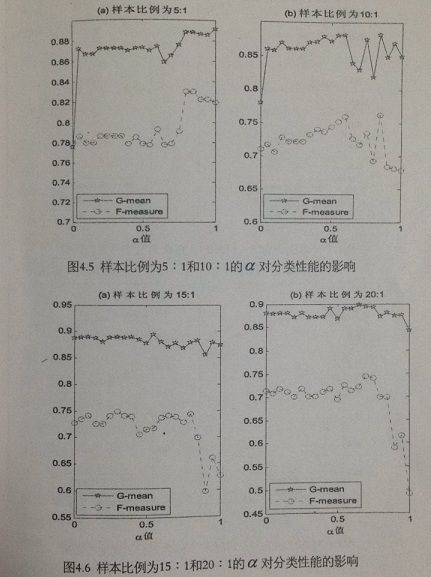
比较算法在不同比例下的 F-measure 性能和 G-mean 性能，测试结果如下所示：

从图中可知：ODR-BSMOTE-SVM 算法的 G-mean 性能和 F-measure 性能都比 BSMOTE 算法优越，这是因为 ODR-BSMOTE-SVM 算法综合了 BSMOTE 算法和 ODR 算法的优势所决定的。利用 ODR 算法去除多数类中的冗余和噪声，利用 BSMOTE 算法对边界少数类进行过抽样，增强了少数类样本为 SVM 分类器提供的信息。

图中可以看出，当不均衡数据比例较小时，ODR-BSMOTE-SVM 与 BSMOTE-SVM 算法相比优越性能显著，这时 ODR 算法体现出它的优越性能，去除多数类样本对分类性能影响较大。而随着样本比例的增加，由于 α 值固定，那么需要利用 ODR 算法进行删除的多数类就会增多，从而导致一些有用的多数类信息被去除，对后续的 SVM 算法不理，所以在 α 值固定的情况下， ODR 算法随着样本类别比例的增大对 SVM 算法分类性能的提高影响很小。

---

参数 a 对算法性能的影响

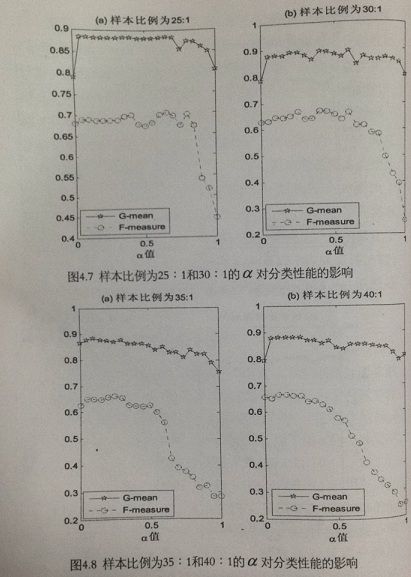
从图4.5 - 4.8 中可以得到：当 α 在 0 附近时，当 α 增大时，算法分类性能有所提高，因为当 α 为 0 时，整个算法就是 BSMOTE 算法，没有去除多数类样本中的噪声的影响，所以算法性能没有显著提高。

随着 α 的增大，即采用了 ODR 算法进行欠抽样，因此在这段区间随着 α 值的增大，SVM 算法分类性能也逐渐提高。

当 α 在中间的区间时，算法随 α 值的变化分类性能变化不大

当最后 α 值接近 1 的一段区间中，随着 α 数值的增大，算法的整体分类性能却有所降低，少数类分类性能急剧降低，尤其是对于不均衡程度较大的数据集而言（图中是比例在 25:1以上），这是由于在这段区间里，当 α 值越大利用 ODR 算法进行大量的多数类样本欠抽样，根据 ODR 算法按参数逐级递减优化的机制，无疑会导致部分有用信息的损失，降低了原有多数样本的空间代表性进而影响 SVM 分类算法的性能。

• 数据集不均衡程度较小时，在参数 α 值接近 1 时，算法的分类性能还是有所提升
• 数据集不均衡程度中等时，在参数 α 值从 0.9 开始时，算法的分类性能持续下降
• 数据集不均衡程度较大时，在参数 α 值在区间 （0.3,1）中时，算法性能随着 α 值增大而降低

通过整体的考虑，最适合的初始参数 α 值为 0.2。通过该实验可以表明当选取合适的 α 值时，可以得到分类效果最优的 ODR-BSMOTE-SVN 算法。