图的邻接表表示及拓扑排序
图的定义
- 图(graph) G=(V, E) G = ( V , E ) ,由顶点(vertex)集 V V 和边(edge)集 E E 组成。每条边为一个点对 (v, w) ( v , w ) 。
图的表示
- ① 邻接矩阵表示法:使用一个二维数组A,对每条边(u, v), A[u][v]=1;否则为0。总空间大小为 O(|v|2) O ( | v | 2 ) 。
邻接矩阵表示法很多情况下浪费空间。所以引出, - ②邻接表表示法:每个顶点使用一个表来存放其所有邻接的点。空间需求为 O(|V|+|E|) O ( | V | + | E | ) 。邻接表是图的标准表示方法。
创建图类及其顶点类
- 首先定义一个顶点类,简单起见,其属性包含:顶点关键字值、顶点的入度、顶点的邻接表
顶点类模板
template<class T>
class Vertex { // 创建一个顶点类表示图的顶点
public:
T data; // 顶点包含的T类型的关键字值
vector- 图类包含一个点集合(用Vertex类型数组表示)以及其他成员函数
template<class T>
class Graph { // 创建一个图类
public:
Vertex* Vlist; // 包含顶点对象的数组
Graph(int n); // 构造函数
Graph(const Graph &g); // 复制构造函数
Graph& operator = (const Graph &g); // 重载=运算符
void DeleteVertex(int index); // 删除某个顶点
int findZeroIndegreeVertexIndex(); // 寻找入度为0的顶点在图中的下标
void Topsort(); // 图的拓扑排序实现方式1
void Topsort1(); // 图的拓扑排序实现方式2,借助队列
private:
int size; // 图的顶点个数
}; 图的拓扑排序
- 拓扑排序是对有向无圈图的顶点的一种排序,如果存在一条点 vi, v i , 到 vj v j 的路径,则拓扑排序使得 vi v i 出现在 vj v j 之前。
- 一个简单的求拓扑排序的方法:先任意找一个入度为0的顶点。然后将该顶点与和它相连的边从图中删除。继续在余图中进行。
- 例如:
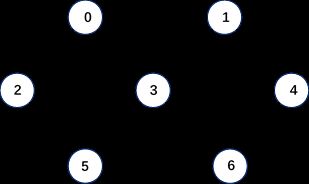
- 上图中,第一个入度为0的顶点为“0”,把该顶点及与之相连的边删除,则入度为0的点为“1”,依次进行……
- 最终该图的拓扑排序为:0->1->4->3->2->6->5或0->1->4->3->6->2->5
图的拓扑排序实现方法1
template<class T>
void Graph::Topsort()
{
int index; // 临时变量表示入度为0顶点下标
for (int i = 0;i < size;i++)
{
index = findZeroIndegreeVertexIndex();
cout <<"V"<< Vlist[index].data << "->"; // 打印拓扑排序
// 使用迭代器遍历向量即W的邻接表
for (vector 借助队列实现拓扑排序
- 首先,将入度为0的顶点入队列。当队列不为空时,顶点出队列,遍历该顶点的邻接表,并将与之相邻的点的入度都减1。
- 如果相邻点入度减1之后为0,则相邻点入队列……这样,出队列的顺序就是拓扑排序的顺序。
图的拓扑排序实现方法2
template<class T>
void Graph::Topsort1()
{
Vertex W;
queue 附图的邻接表示及拓扑排序C++实现代码
#include* Vlist; // 包含顶点对象的数组
Graph(int n); // 构造函数
Graph(const Graph &g); // 复制构造函数
Graph& operator = (const Graph &g); // 重载=运算符
void DeleteVertex(int index); // 删除某个顶点
int findZeroIndegreeVertexIndex(); // 寻找入度为0的顶点在图中的下标
void Topsort(); // 图的拓扑排序实现方式1
void Topsort1(); // 图的拓扑排序实现方式2,借助队列
private:
int size; // 图的顶点个数
};
// 图类函数成员实现
template<class T>
Graph::Graph(int n)
{
size = n; // 图的顶点数量
Vlist = new Vertex [size]; // 为包含顶点的数组分配空间
}
template<class T>
Graph::Graph(const Graph &g)
{
this->size = g.size;
this->Vlist = new Vertex[size];
for (int i = 0;i < size;i++) // 深层复制
{
this->Vlist[i] = g.Vlist[i];
}
}
template<class T>
Graph& Graph::operator = (const Graph &g) // 重载=操作符实现
{
this->size = g.size;
this->Vlist = new Vertex [size];
for (int i = 0;i < size;i++)
{
this->Vlist[i] = g.Vlist[i];
}
return *this;
}
template<class T>
int Graph::findZeroIndegreeVertexIndex()
{
for (int i = 0;i < size;i++)
{
if (Vlist[i].Indegree == 0)
return i;
}
}
template<class T>
void Graph::Topsort()
{
int index; // 临时变量表示入度为0顶点下标
for (int i = 0;i < size;i++)
{
index = findZeroIndegreeVertexIndex();
cout <<"V"<< Vlist[index].data << "->"; // 打印拓扑排序
for (vector::Topsort1()
{
Vertex W;
queue - 运行结果
V0->V1->V4->V3->V2->V6->V5->
V0->V1->V4->V3->V2->V6->V5->
请按任意键继续. . .参考资料
Mark Allen Weiss: 数据结构与算法分析