Mahout机器学习平台之聚类算法详细剖析(含实例分析)
第一部分:
学习Mahout必须要知道的资料查找技能:
学会查官方帮助文档:
解压用于安装文件(mahout-distribution-0.6.tar.gz),找到如下位置,我将该文件解压到win7的G盘mahout文件夹下,路径如下所示:
G:\mahout\mahout-distribution-0.6\docs
学会查源代码的注释文档:
方案一:用maven创建一个mahout的开发环境(我用的是win7,eclipse作为集成开发环境,之后在Maven Dependencies中找到相应的jar包《这些多是.class文件》,记得将源代码文件解压到自己硬盘的一个文件夹中,之后填写源代码的文件路径即可)
方案二:直接用eclipse创建一个java工程,将解压缩的源代码文件添加到这个工程,既可以查看。
Mahout官网:
http://mahout.apache.org/
https://builds.apache.org/job/Mahout-Quality/javadoc/
Mahout中的Shell命令进行操作:
/bin/mahout 方法名 -h
第二部分:
数据挖掘(机器学习)——聚类算法的简介(怎样使用各种聚类算法):
1. 选择聚类算法,所面临的常见问题又哪些?
1)不同形状的数据集。不同形状的数据集,也需要采取不同的度量策略,或者不同的聚类算法。
2)不同的数据次序。相同数据集,但数据输入次序不同,也会造成聚类的结果的不同。
3)噪声。不同的算法,对噪声的敏感程度不同。
2. 在高维的欧式空间,什么是“维数灾难”?
在高维下,所有点对的距离都差不多(如欧式距离),或者是几乎任意两个向量都是正交(利用夹角进行进行度量),这样聚类就很困难。
3. 常见的聚类算法的策略有哪些?
1)层次或凝聚式聚类。采取合并的方式,将邻近点或簇合并成一个大簇。
2)点分配。每次遍历数据集,将数据分配到一个暂时适合的簇中,然后不断更新。
4. 层次聚类算法的复杂度是多少?
每次合并,都需计算出两个点对之间的距离,复杂度是O(n^2),后续步骤的开销,分布正比与O((n-1)^2), O((n-2)^2)...,这样求和算下来,算法复杂度是O(n^3).
算法优化:
采用优先队列/最小堆来优化计算。优先队列的构建,第一步需要计算出每两个点的距离,这个开销是O(N^2).一般情况下,N个元素,单纯的优先队列的构建开销为O(N),若是N^2个距离值,则建堆的开销是O(N^2)。
第二步,合并,合并需要一个删除、计算和重新插入的过程。因为合并一个簇对,就需要更新N个元素,开销为O(N*logN)。总的开销为O((N^2) * logN).
所以,总的算法复杂度为O((N^2) * logN).
5. 欧式空间与非欧式空间下,常见的簇之间的距离度量有哪些?
欧式空间:
1)两个簇之间的质心之间的距离最小
2)两个簇中所有点之间的最短距离
3)两个簇之间所有点对的平均距离
4)将具有最小半径的两个簇进行合并,簇的半径:簇内的点到质心的最大距离
5)将具有最小直径的两个簇进行合并,簇的直径:簇内任意两点间的最大距离
非欧式空间,簇的中心点定义,该点距离其他点的距离最近,如何计算?
1)该点到簇中其他所有点的距离之和(求和),1-范数
2)该点到簇中其他点的最大距离(最大值),无穷-范数
3)该点到簇中其他点的平方和(平方和),2-范数
6. k-means、k均值算法
点分配式的聚类算法。一般用于球形或凸集的数据集。
算法步骤如下:
1)初始化k个选择点作为最初的k个簇的中心
2)计算每个点分别到k个簇的中心,并将点分配到其距离最近的簇中
3)由分配的点集,分别更新每个簇的中心,然后回到2,继续算法,直到簇的中心变化小于某个阈值
7. k-means算法的两个问题?
1)初始化选择点;常用的方式是尽量选择距离比较远的点(方法:依次计算出与已确定的点的距离,并选择距离最大的点),或者首先采取层次聚类的方式找出k个簇
2)如何选取k值;k值选取不当,会导致的问题?当k的数目低于真实的簇的数目时,平均直径或其他分散度指标会快速上升可以采用多次聚类,然后比较的方式。多次聚类,一般是采用1, 2, 4, 8...数列的方式,然后找到一个指标在v/2, v时,获取较好的效果,然后再使用二分法,在[v/2, v]之间找到最佳的k值。
8. CURE算法
使用场景:
任何形状的簇,如S形、环形等等,不需要满足正态分布,欧式空间,可以用于内存不足的情况
特征:
簇的表示不是采用质心,而是用一些代表点的集合来表示。
算法步骤:
1)初始化。抽取样本数据在内存中进行聚类,方法可以采用层次聚类的方式,形成簇之后,从每个簇中再选取一部分点作为簇的代表点,并且每个簇的代表点之间的距离尽量远。对每个代表点向质心移动一段距离,距离的计算方法:点的位置到簇中心的距离乘以一个固定的比例,如20%。
2)对簇进行合并。当两个簇的代表点之间足够近,那么就合并这两个簇,直到没有更足够接近的簇。
3)点分配。对所有点进行分配,即将点分配给与代表点最近的簇。
9. GRGPF算法
场景:
非欧式空间,可用于内存不足的情况(对数据抽样)
特征:
同时使用了层次聚类和点分配的的思想。
如何表示簇?
数据特征:簇包含点的数目,簇中心点,离中心点最近的一些点集和最远的一些点集,ROWSUM(p)即点p到簇中其他店的距离平方和。靠近中心的点集便于修改中心点的位置,而远离中心的点便于对簇进行合并。
簇的组织:类似B-树结构。首先,抽取样本点,然后做层次聚类,就形成了树T的结构。然后,从树T中选取一系列簇,即是GRGPF算法的初始簇。然后将T中具有相同祖先的簇聚合,表示树中的内部节点。
点的分配:对簇进行初始化之后,将每个点插入到距离最近的那个簇。
具体处理的细节更为复杂,如果对B-树比较了解,应该有帮助。
10. 流聚类,如何对最近m个点进行聚类?
N个点组成的滑动窗口模型,类似DGIM算法中统计1的个数。
1)首先,划分桶,桶的大小是2的次幂,每一级桶的个数最多是b个。
2)其次,对每个桶内的数据进行聚类,如采用层次聚类的方法。
3)当有新数据来临,需要新建桶,或者合并桶,这个类似于GDIM,但除了合并,还需要合并簇,当流内聚类的模型变化不是很快的时候,可以采取直接质心合并的方式。
4)查询应答:对最近的m个点进行聚类,当m不在桶的分界线上时,可以采用近似的方式求解,只需求出包含m个点的最少桶的结果。
第三部分:
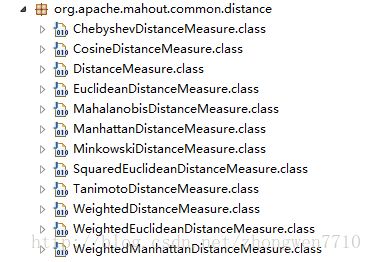
Mahout中实现常用距离的计算:以下摘自mahout-core-0.6.jar包中
对以上进行距离进行解析:
皮尔森相关度
类名:PearsonCorrelationSimilarity
原理:用来反映两个变量线性相关程度的统计量
范围:[-1,1],绝对值越大,说明相关性越强,负相关对于推荐的意义小。
说明:1、不考虑重叠的数量;2、如果只有一项重叠,无法计算相似性(计算过程被除数有n-1);3、如果重叠的值都相等,也无法计算相似性(标准差为0,做除数)。
该相似度并不是最好的选择,也不是最坏的选择,只是因为其容易理解,在早期研究中经常被提起。使用Pearson线性相关系数必须假设数据是成对地从正态分布中取得的,并且数据至少在逻辑范畴内必须是等间距的数据。Mahout中,为皮尔森相关计算提供了一个扩展,通过增加一个枚举类型(Weighting)的参数来使得重叠数也成为计算相似度的影响因子。
欧式距离相似度
类名:EuclideanDistanceSimilarity
原理:利用欧式距离d定义的相似度s,s=1 / (1+d)。
范围:[0,1],值越大,说明d越小,也就是距离越近,则相似度越大。
说明:同皮尔森相似度一样,该相似度也没有考虑重叠数对结果的影响,同样地,Mahout通过增加一个枚举类型(Weighting)的参数来使得重叠数也成为计算相似度的影响因子。
余弦相似度
类名:PearsonCorrelationSimilarity和UncenteredCosineSimilarity
原理:多维空间两点与所设定的点形成夹角的余弦值。
范围:[-1,1],值越大,说明夹角越大,两点相距就越远,相似度就越小。
说明:在数学表达中,如果对两个项的属性进行了数据中心化,计算出来的余弦相似度和皮尔森相似度是一样的,在mahout中,实现了数据中心化的过程,所以皮尔森相似度值也是数据中心化后的余弦相似度。另外在新版本中,Mahout提供了UncenteredCosineSimilarity类作为计算非中心化数据的余弦相似度。
Spearman秩相关系数
类名:SpearmanCorrelationSimilarity
原理:Spearman秩相关系数通常被认为是排列后的变量之间的Pearson线性相关系数。
范围:{-1.0,1.0},当一致时为1.0,不一致时为-1.0。
说明:计算非常慢,有大量排序。针对推荐系统中的数据集来讲,用Spearman秩相关系数作为相似度量是不合适的。
曼哈顿距离
类名:CityBlockSimilarity
原理:曼哈顿距离的实现,同欧式距离相似,都是用于多维数据空间距离的测度
范围:[0,1],同欧式距离一致,值越小,说明距离值越大,相似度越大。
说明:比欧式距离计算量少,性能相对高。
Tanimoto系数
类名:TanimotoCoefficientSimilarity
原理:又名广义Jaccard系数,是对Jaccard系数的扩展,等式为
范围:[0,1],完全重叠时为1,无重叠项时为0,越接近1说明越相似。
说明:处理无打分的偏好数据。
对数似然相似度
类名:LogLikelihoodSimilarity
原理:重叠的个数,不重叠的个数,都没有的个数
范围:具体可去百度文库中查找论文《Accurate Methods for the Statistics ofSurprise and Coincidence》
说明:处理无打分的偏好数据,比Tanimoto系数的计算方法更为智能。
参考网址:http://www.cnblogs.com/dlts26/archive/2012/06/20/2555772.html
Mahout中聚类实现的算法:
官网算法Clustering算法摘录:
· Canopy Clustering -single machine/MapReduce (deprecated, will beremoved once Streaming k-Means is stable enough)
· k-Means Clustering -single machine / MapReduce
· Fuzzy k-Means -single machine / MapReduce
· Streaming k-Means -single machine / MapReduce
· Spectral Clustering -MapReduce
官网参考网址:http://mahout.apache.org/users/basics/algorithms.html
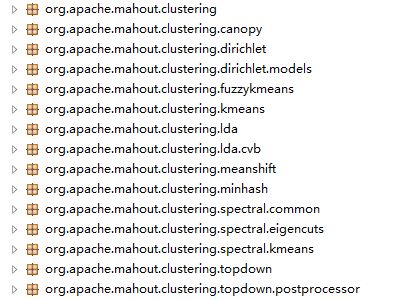
源代码中聚类算法的实现:以下摘自mahout-core-0.6.jar包中
对以上各种聚类类的解析:
第四部分:
用Mahout进行实例分析(K-means、canopy、fuzzy k-means)
| 步骤简介: A、数据转换及相应的命令简介 B、K-means、canopy、fuzzy k-means命令,参数简介 C、mahout操作k-means、canopy、fuzzy k-means聚类的详细命令 D、用K-means算法进行操作,之后用R进行可视化操作 |
详细步骤:
A、数据转换及相应的命令简介
Mahout类:org.apache.mahout.clustering.conversion.InputDriver
作用:这个类,是将文本文件中(.txt格式)用空格分隔的浮点型数字转换为Mahout中的序列文件(VectorWritable类型),这个类型适合集群任务,有些Mahout任务,则需要任务是一般类型。
源代码的位置:mahout-integration-0.6.jar
命令使用:mahoutorg.apache.mahout.clustering.conversion.InputDriver http:// \
–i /user/hadoop/mahout6/p04-17.txt \
-o /user/hadoop/mahout6/vecfile \
-v org.apache.mahout.math.RandomAccessSparseVector
数据集下载:p04-17.txt
对于文本数据,数据处理及相关的类(注解:文本转换为序列文件,序列文件转换为向量文件,下面几个类,主要是对文本文件进行挖掘时用):
向量文本类型(向量文件的存储方式):
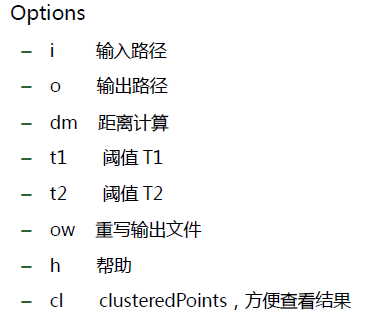
B、K-means、canopy、fuzzy k-means命令,参数简介
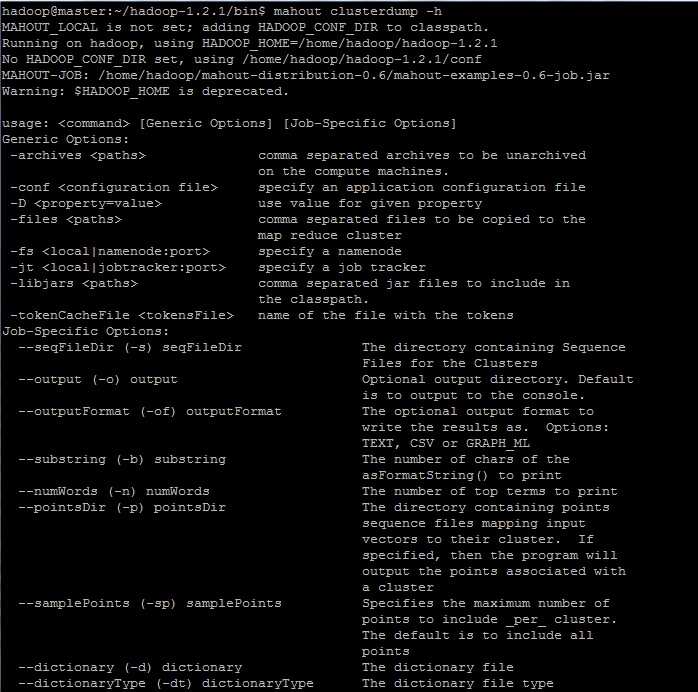
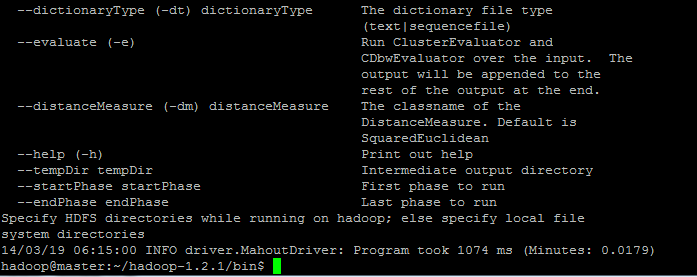
Mahout之k-means命令使用参数简介:
Mahout之canopy命令使用参数简介:
Mahout之fuzzy k-means命令使用参数简介:
C、mahout操作k-means、canopy、fuzzy k-means聚类的详细命令
Mahout之数据预处理:
mahoutorg.apache.mahout.clustering.conversion.InputDriver \
–i /user/hadoop/mahout6/p04-17.txt \
-o /user/hadoop/mahout6/vecfile \
-v org.apache.mahout.math.RandomAccessSparseVector
Mahout之k-means命令:
mahout kmeans -i /user/hadoop/mahout6/vecfile -o/user/hadoop/mahout6/result1 -c /user/hadoop/mahout6/clu1 -x 20 -k 2 -cd 0.1-dm org.apache.mahout.common.distance.SquaredEuclideanDistanceMeasure -cl
Mahout之canopy命令:
mahout canopy -i /user/hadoop/mahout6/vecfile -o /user/hadoop/mahout6/canopy-result-t1 1 -t2 2 –ow
Mahout之fuzzy k-means命令:
mahoutfkmeans -i /user/hadoop/mahout6/vecfile
-o/user/hadoop/mahout6/fuzzy-kmeans-result
-c/user/hadoop/mahout6/fuzzy-kmeans-centerpt -m 2 -x 20 -k 2 -cd 0.1
-dmorg.apache.mahout.common.distance.SquaredEuclideanDistanceMeasure -ow -cl
D、用K-means算法进行操作,之后用R进行可视化操作(导出K-means算法生成的数据)
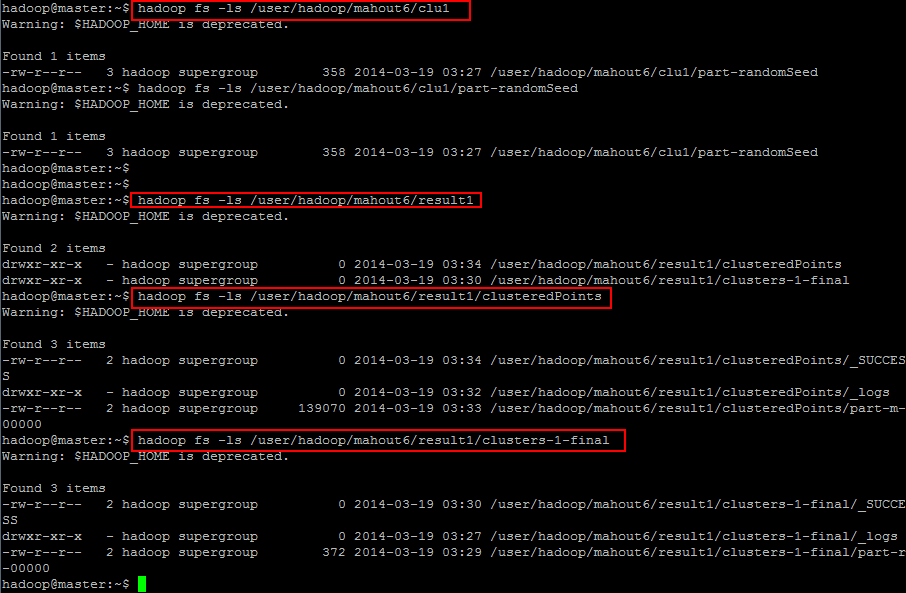
聚类结果分析:
数据导出命令帮助文档信息:
实例命令行如下所示(本案例脚本是用mahout之k-means算法生成的数据导出):
将数据转换为CSV格式:
mahoutclusterdump -s /user/hadoop/mahout6/result2/clusters-1-final -p/user/hadoop/mahout6/result2/clusteredPoints -o /home/hadoop/cluster1.csv -ofCSV
将数据转换为TXT格式:
mahoutclusterdump -s /user/hadoop/mahout6/result2/clusters-1-final -p/user/hadoop/mahout6/result2/clusteredPoints -o /home/hadoop/cluster1.txt -ofTEXT
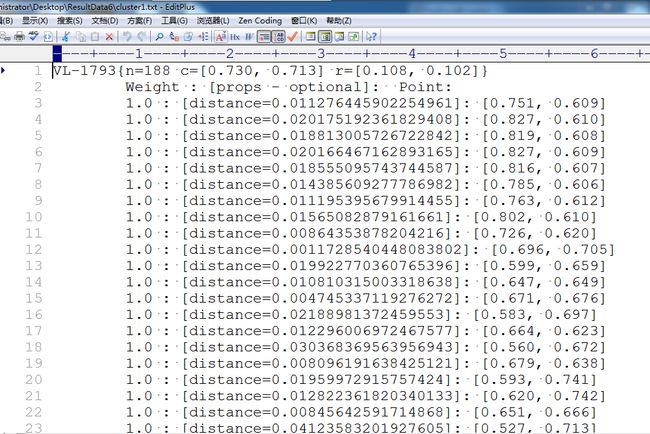
导出后的数据格式:
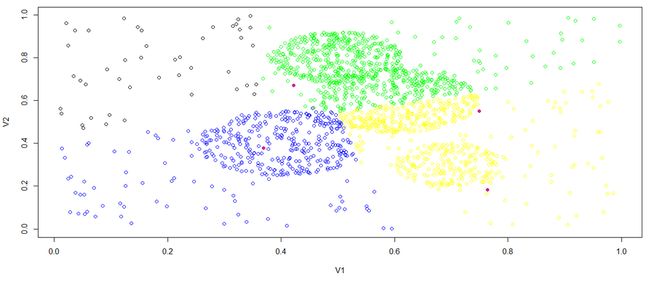
用R语言进行效果展示(输出的数据格式可以参考上图所示):
mahoutkmeans -i /user/hadoop/mahout6/vecfile -o /user/hadoop/mahout6/resultTest2 -c/user/hadoop/mahout6/cluTest1-x 20 -cd 0.00001 -dmorg.apache.mahout.common.distance.SquaredEuclideanDistanceMeasure -cl
mahoutclusterdump -s /user/hadoop/mahout6/result2/clusters-1-final -p/user/hadoop/mahout6/result2/clusteredPoints -o /home/hadoop/cluster1.csv -ofCSV
将上面聚类生成的四个数据进行处理,分成四个文件,之后按如下R代码进行可视化处理:
R参考代码:
| > c1<-read.csv(file=\"2/cluster1.csv\",sep=\",\",header=FALSE) > c2<-read.csv(file=\"2/cluster2.csv\",sep=\",\",header=FALSE) > c3<-read.csv(file=\"2/cluster3.csv\",sep=\",\",header=FALSE) > c4<-read.csv(file=\"2/cluster4.csv\",sep=\",\",header=FALSE) > y<-rbind(c1,c2,c3,c4) > cols<-c(rep(1,nrow(c1)),rep(2,nrow(c2)),rep(3,nrow(c3)),rep(4,nrow(c4))) > plot(y, col=c(\"black\",\"blue\")[cols]) > q() > plot(y, col=c(\"black\",\"blue\",\"green\",\"yellow\")[cols]) > center<-matrix(c(0.764, 0.182,0.369, 0.378,0.749, 0.551,0.422, 0.671),ncol=2,byrow=TRUE) > points(center, col=\"violetred\", pch = 19) |
第四部分:
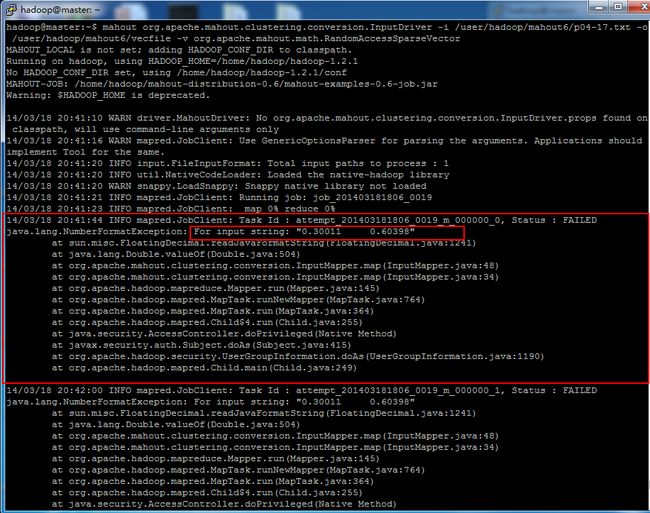
数据预处理遇到的问题(输入如下命令报错):
mahoutorg.apache.mahout.clustering.conversion.InputDriver \
–i /user/hadoop/mahout6/p04-17.txt \
-o /user/hadoop/mahout6/vecfile \
-v org.apache.mahout.math.RandomAccessSparseVector
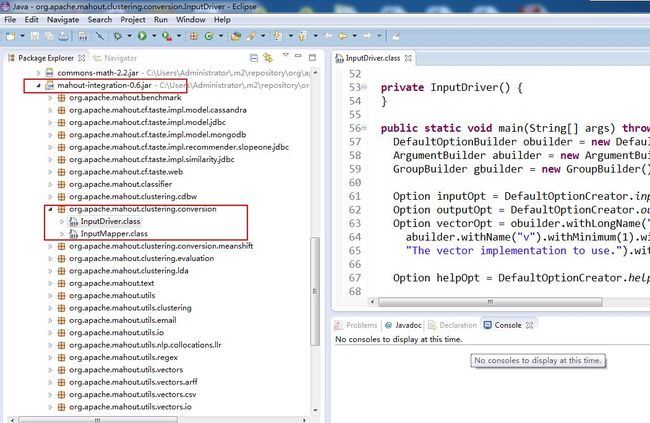
这个类(mahoutorg.apache.mahout.clustering.conversion.InputDriver)位置位于源代码中的mahout-integration-0.6.jar的jar包下,如上图所示:
英文解析:(摘录源码注释文件)
This class converts text files containing space-delimited floating point numbers intoMahout sequence files of VectorWritable suitable for input to the clusteringjobs in particular, and any Mahout job requiring this input in general.
中文解析:(摘自源码注释文件)
这个类,是将文本文件中(.txt格式)用空格分隔的浮点型数字转换为Mahout中的序列文件(VectorWritable类型),这个类型适合集群任务,有些Mahout任务,则需要任务是一般类型。
mahout org.apache.mahout.clustering.conversion.InputDriver在源代码中的位置:
参考文献:
http://mahout.apache.org/
https://builds.apache.org/job/Mahout-Quality/javadoc/
http://f.dataguru.cn/thread-281665-1-1.html
http://blog.csdn.net/viewcode/article/details/9146965
http://mahout.apache.org/users/basics/algorithms.html
http://mahout.apache.org/users/clustering/k-means-clustering.html
http://mahout.apache.org/users/clustering/canopy-clustering.html
http://mahout.apache.org/users/clustering/fuzzy-k-means.html
http://mahout.apache.org/users/clustering/cluster-dumper.html
http://mahout.apache.org/users/clustering/k-means-commandline.html
http://mahout.apache.org/users/clustering/canopy-commandline.html
http://mahout.apache.org/users/clustering/fuzzy-k-means-commandline.html