相关性的基本概念「AI基础」

小结关注：决策智能与机器学习，深耕AI脱水干货

作者 |  Cassie Kozyrkov

来源 | towardsdatascience

导言：因果关系通过来自于严禁的试验设计和分析，但如果没有得到因果关系，那么你所拥有的只有关联性。相关性是什么?特别强调，关联性不是因果关系！！！！

当然，你可能已经听到我们的统计学家对你大喊大叫了。但什么是相关性呢?它是指数据集中的变量看起来以某种方式在一起变化。

如果两个变量X和Y以某种方式一起运动，那么它们就是相关的。

数学定义：

不完美的线性相关

例如，“X越高，Y越高”(称为正相关)或“X越高，Y越低”(称为负相关)。

如果你正在寻找(人口)相关性的公式，维基百科有你需要的一切。但如果你想这样做，为什么不直接去呢?你为什么在这里?你想要直观的解释吗?酷。这里有一个山:

在左边，高度和(从左到右)距离正相关。一个上升，另一个也上升。在右侧，高度和距离呈负相关

当大多数人听到相关性这个词时，他们倾向于认为是完美的线性相关性：

在山上向右迈一步(X)，在同一山坡上的任何地方，海拔高度的变化(Y)都是相同的。只要你从左到右向上(正相关)，就不会出现令人惊讶的锯齿/弯曲。

记住，只有当你从左到右徒步旅行时，向上才是积极的，就像你读英语一样。如果你从右边接近希尔斯，统计学家将不知道如何处理你。我想统计学家试图告诉你的是，永远不要向右靠近。那只会把我们弄糊涂。

但如果你正确地徒步旅行，那么“向上”就是“积极的”。

在现实中，这座山并不是完美的，所以高度和距离的相关幅度小于100%。(你会在前面加上+/-取决于是上升还是下降，所以相关性在-1和1之间。这是因为它的公式(粘贴在上面的维基百科)除以标准差，从而消除了每个变量离散度的大小。如果没有这个分母，你会发现无论你用英寸还是厘米来测量身高，这种关系的强度都是一样的。每当你看到统计中的缩放/归一化，它通常是用来帮助你比较用不同单位衡量的苹果和橘子的。)

不相关的变量

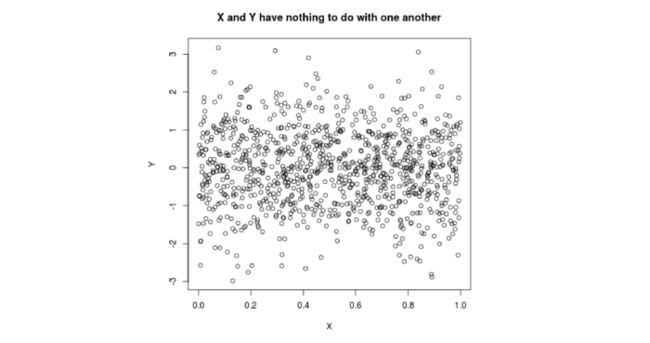
零的相关性是什么样子的?你是在想一个里面没有可辨别的图案的凌乱的云吗?喜欢的东西:

当然,工作。你知道我怎么知道X和Y真的没有关系吗?因为我就是这样创造它们的。如果您想模拟两个不相关变量的类似图，请尝试在R online中运行以下基本代码片段:

X <- runif(100) # 100 regular random numbers between 0 and 1
Y <- rnorm(100) # Another 100 random numbers from bell curve
plot(X, Y, main = "X and Y have nothing to do with one another")

但还有另一种方法。关系越不线性，你的相关性就越接近于零。事实上，如果你把这座山看作一个整体(而不是每次只看一个斜率)，你会发现两者之间的相关性为零，尽管高度和距离之间有明显的关系(这就是一座山)。

X <- seq(-1, 1, 0.01) # Go from -1 to 1 in increments of 0.01
Y <- -X^2 # Secret formula for the ideal hill
plot(X, Y, main = "The linear correlation is zero")
print(cor(X, Y)) # Check the correlation is zero

小结

总而言之，如果你想谈论因果关系，你需要一个验证实验。没有实验，你所拥有的只有相关性，对于许多决策——基于因果推理的决策——相关性是远远不够的。

交流合作

请加微信号：yan_kylin_phenix，注明姓名+单位+从业方向+地点，非诚勿扰。