数据结构：图（二） 图的重要操作——遍历

图的重要操作——遍历

遍历：从已给连通图中的某一顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次，就叫做图的遍历，它是图的最重要的基本运算

遍历图的实质：找每个顶点的邻接点并访问的过程。

 

注意：图的遍历比树更复杂，因为元素之间的关系复杂。

要考虑两种情况：

①可能会陷入死循环（如果图中存在环）

②可能有的顶点不能从出发点访问到（比如存在孤立点的非连通图）

针对上面的两个问题，处理的方法就是对每个顶点做一个访问标志。比如设置一个辅助数组visited[n]，用来标记每个被访问过的顶点。它的初始状态是0，在图的遍历过程中，一旦某一个顶点vi被访问，visited[i]置为1，防止它被多次访问。

 

图的遍历方式分为深度优先搜索（简称深度遍历，Depth_First Search：DFS）和广度优先搜索（简称广度遍历，Breadth_First Search：BFS）

1.图的深度遍历：DFS

（1）遍历方式：假设图为G=(V,E)，从v0开始深度优先遍历图。大致的访问过程是：

访问v0，作已访问标志——>选择一个与v0邻接但未访问的顶点u（（如果没有，则从v0 开始的深度优先遍历结束；如果有多个，选其中一个）——>从顶点u开始深度优先遍历图

（2）特点：类似于树的前序遍历；沿着图的某一分支访问，直到它的末端，然后回溯。

举个例子：

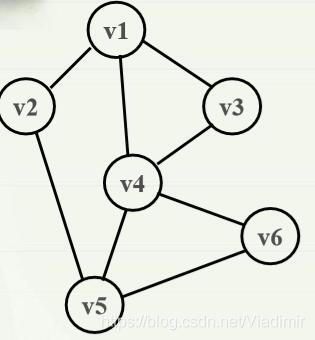
无向图：

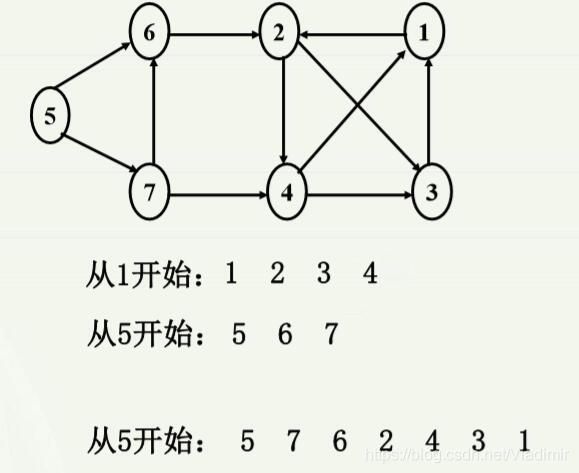
有向图：

（3）算法

从某一顶点v深度遍历图G：

void DFS (Graph& G, T v, bool &visited[])
{ //从顶点v开始深度优先遍历图G 
    visite(v);   //访问顶点v 
    i= G.getVertexPos(v); //顶点v的存储位置 
    visited[i] = true; //作访问标记 
    T w = G.getFirstNeighbor(v); //v的第一个邻接顶点 
    k=G.getVertexPos(w); while (k != -1) { 
        //若邻接顶点w存在 
        if ( !visited[k] ) DFS(G, w, visited);  //若w未访问过, 递归访问顶点w 
        w = G.getNextNeighbor (v, w); //下一个邻接顶点 
        k=G.getVertexPos(w);  
    } 
};

深度优先遍历图G（所有顶点都将被作为起始点）：

void DFS_Graph (Graph& G) 
{ //深度优先遍历图（图可能不连通或从一个顶点不能遍历） 
    int i, loc, n = G.NumVertices(); //顶点个数 
    bool *visited = new bool[n];  //创建辅助数组 
    for (i = 0; i < n; i++) 
        visited [i] = false; //辅助数组visited初始化 
    for(i=0;i

（上面的两段代码，需要与完整的图ADT的代码结合起来才能运行，这里只是给大家展示一下，提供一种思路）

 

2.图的广度遍历：BFS

（1）遍历方式：假设图为G=(V,E)，从v0开始广度优先遍历图。大致的访问过程是：

访问v0，作为以访问的标志——>依次访问与v0邻接但未访问的各个顶点——>再依次访问这些顶点的未被访问的邻接点。。。

（2）特点：类似于树的层次遍历。尽可能先在横向上访问邻接点，即由远及近，依次访问和出发点有路径相通且路径长度为1,2....的顶点。

举个例子：

上面这个是无向图的，下面再举一个有向图的例子：

（3）需要注意的问题

①在没有给出图的存储时，图的某种遍历方式得到的遍历序列可能是不唯一的；

②从某顶点开始遍历图，不一定能访问到图中的所有元素；（只能访问到该顶点所在最大连通子图（连通分量）的所 有顶点。（有的图可能有的顶点是孤立的，不与图中其他任何顶点有关联））

③对于连通无向图，遍历访问了n个元素，经过了n-1条边， 它们组成的子图就是生成树。（当然，根据遍历方式不同，可以组成深度生成树和广度生成树）；对于非连通无向图，遍历可得到连通分量的生成树森林（通俗点来说就是会生成好多棵生成树）。

深度生成树和广度生成树举例：

广度生成树：（从v1开始）

深度生成树：（从v1开始）

（4）算法

从某一顶点v广度遍历图G：

void BFS (Graph& G, const T& v) 
{ //从顶点v开始广度优先遍历图G 
    int i, w, n = G.NumVertices(); //图中顶点个数 
    bool *visited = new bool[n]; 
    for (i = 0; i < n; i++) visited[i] = false; 
    int loc = G.getVertexPos (v); //取顶点号 
    visite(v);  //访问顶点v 
    visited[loc] = true; //做已访问标记 
    Queue  Q; 
    Q.EnQueue (v);        //顶点进队列, 实现分层访问
    while (!Q.IsEmpty() ) { //循环, 访问所有结点 
        Q.DeQueue (v); 
        k = G.getFirstNeighbor (v); //第一个邻接顶点 
        while (k != -1) { //若邻接顶点w存在 
            if (!visited[k]) { //若未访问过 
                visite(w); //访问 
                visited[k] = true; 
                Q.EnQueue (w); } //顶点w进队列 
            k = G.getNextNeighbor (v, w); //找顶点loc的下一个邻接顶点 
        }            
    } //外层循环，判队列空否 delete [] visited;
}