01-复杂度1 最大子列和问题

记录:

题目如下:

给定K个整数组成的序列{ N​1​​, N​2​​, ..., N​K​​ }，“连续子列”被定义为{ N​i​​, N​i+1​​, ..., N​j​​ }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

• 数据1：与样例等价，测试基本正确性；
• 数据2：102个随机整数；
• 数据3：103个随机整数；
• 数据4：104个随机整数；
• 数据5：105个随机整数；

输入格式:

输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。

输出格式:

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

6
-2 11 -4 13 -5 -2

输出样例:

20

 

下面我们开始分析:

• 算法1:

简单无脑暴力循环法:

最外层循环 和 中间循环用变量i和j分别控制数组中的首尾位置，当i=0时，j从0到末尾n；当i=1时，j从1到末尾n；......

最里层循环，变量k负责从i到j之间的变化，这样就可以计算i和j之间数的总和。

int MaxSubseqSum(int A[],int n){ //A是测试数组 n是数组长度
int maxSubseq  = 0;
int thisSubseq = 0;
for (int i = 0; i < n; ++i){
    for (int j = i; j < n; ++j){
        thisSubseq = 0;
        for (int k = i; k <= j; ++k){
            thisSubseq += A[k];
        }
        if (thisSubseq > maxSubseq){ //如果当前总和 大于 记录的总和则把其赋值给最大总和
            maxSubseq = thisSubseq;
        }
    }
}
if (maxSubseq < 0){
    return 0 ;
}else
return maxSubseq;
}

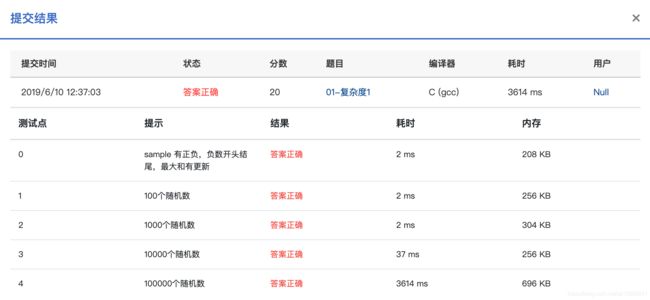
但是这种算法嵌套了三层循环，时间复杂度为O(N^3)，当数据量很大的时候效率就会很低，如下图，在大的数据量下就会超时。

 

• 算法2：

第二种方法是把算法1的最里层循环省略，因为k是负责计算i和j之间的数的和，仔细观察k发现每次都会重新累加从i到j。然而我们只需要在j下直接加上j+1，就可以得到下一个循环的数和，而不用每次都去从新累加。因此优化算法为：

int MaxSubseqSum(int A[],int n){
int maxSubseq  = 0;
int thisSubseq = 0;
for (int i = 0; i < n; ++i){
    thisSubseq = 0;
    for (int j = i; j < n; ++j){
        thisSubseq += A[j];    //每次累加A[j] 相当于 之前k变量从i加到j
        if (thisSubseq > maxSubseq){ //当前累加数 超过 记录的最大总和时 直接替换
        maxSubseq = thisSubseq;
    }
    }
}
if (maxSubseq == 0){
    return 0;
}else
return maxSubseq;
}

该优化算法的时间复杂度为O(N^2)，看起来效率高了不少，但是看下图，当数据量很大时，运行时间还是有点吓人的。

• 算法3：

我们看还能不能再次优化算法了：

int MaxSubseqSum(int A[],int n){
int maxSubseq  = 0; //记录最大总和
int thisSubseq = 0; //记录当前总和
for (int i = 0; i < n; ++i){
    thisSubseq += A[i];
    if (thisSubseq > maxSubseq){
        maxSubseq = thisSubseq;
    }else if (thisSubseq < 0){
//计算数组从头到尾的和，当thisSubseq变量的和小于0时,意味着再往后加数只会变小，所以重置为0，重新计算
        thisSubseq = 0;
    }
}
if (maxSubseq < 0){
    return 0;
}else
return maxSubseq;
}

这么神奇，只用了一层循环就搞定了，时间复杂度只有O(N)。

运行时间竟然只有这么少:

• 算法4：

用一个新的思想：分而治之。

将一个数组从中间拆分为2，再次将拆分完的2个数组从中间拆分为4，如此循环，直至拆到不能拆分为止。

然后分别求拆分线两边的最大值，以及跨越拆分线的最大值，将拆分线左边的最大值，右边最大值，跨越拆分线的最大值进行比较，最大的那一个就是最大的连续子数组。

对于题目来说，该算法不是最优的，但是这种将大的问题拆分成小问题的思想很好。

int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}
 
int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
 
    int LeftBorderSum, RightBorderSum;
    int center, i;
 
    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }
 
    /* 下面是"分"的过程 */
    center = ( left + right ) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
 
    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */
 
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */
 
    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}