强化学习入门(四):Q-learning算法系列1:基本思想
文章目录
- 一、基本思想
- 1、基本介绍
- 1、critic
- 2、状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s)
- 2、状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s)的评估
- 1、基于蒙特卡洛的方法Monte-Carlo (MC)
- 2、时序分差方法Temporal-difference (TD)
- 3、MC与TD比较
- 3、Q-Learning基本原理
- 1、另一个crtic——状态-行动价值函数 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)
- 2、实现步骤
- 3、怎么判定 π ′ \pi' π′ 比 π \pi π好呢?
- 4、如何寻找 π ′ \pi' π′ ?
- 5、证明 V π ′ ( s ) > V π ( s ) V^{\pi'}(s)>V^{\pi}(s) Vπ′(s)>Vπ(s)是存在的
- 4、Q-learning的三个使用技巧
- 1、Target network
- 2、Exploration
- 1、Epsilon Greedy
- 2、Boltzmann Exploration
- 3、Replay Buffer
- 5、经典Q-learning实现流程
一、基本思想
1、基本介绍
1、critic
Q-learning 是 value-based 的方法,在这种方法中我们不是要训练一个 policy,而是要训练一个critic网络。critic 并不直接采取行为,只是对现有的 actor π \pi π,评价它的好坏。

2、状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s)
V π ( s ) V^{\pi}(s) Vπ(s)是对于actor π \pi π, 给定状态s,期望得到的累积收益,即在遇到游戏的某个 state 后,采取策略为 π \pi π的actor 一直玩到游戏结束,所能得到的 reward 之和。

V π ( s ) V^{\pi}(s) Vπ(s)的输入是某个state,输出是一个scalar标量。所以该值取决于状态s和actor π \pi π。
2、状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s)的评估
有两种方法:
1、基于蒙特卡洛的方法Monte-Carlo (MC)
critic 观察 π \pi π 进行游戏的整个过程, 直到该游戏回合结束再计算累积收益(通过比较期望收益和实际收益G,来训练critic)
Tip: 有时一个游戏回合可能会很长,这个等到游戏回合结束再计算收益的方法训练起来会花费过长的时间,因此引入另外一种方法 Temporal-difference(TD)
2、时序分差方法Temporal-difference (TD)

即,时序分差算法计算的是两个状态之间的收益差——通过比较期望差异与实际差异r之间的差别来训练critic。
3、MC与TD比较
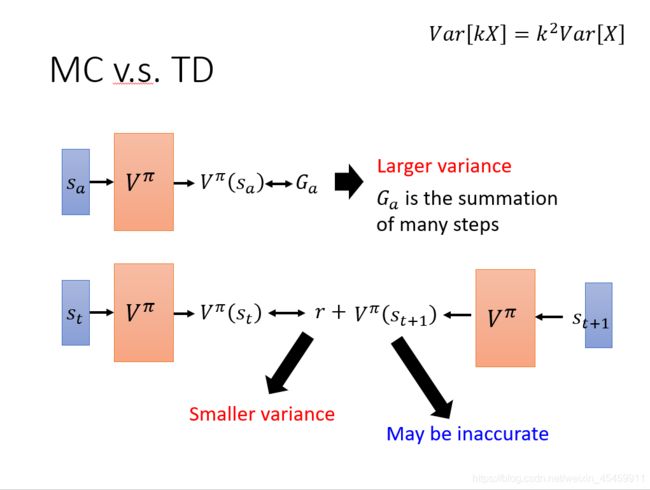
MC 方法的问题在于最后得到的Ga的方差很大(Ga是 在遇到 的情况下使用策略 π \pi π的actor一直玩游戏直到结束得到的实际 reward,是一个随机变量,因为游戏是有随机性的,所以每一次得到Ga是不一样的)。
假设Ga是k步 reward 的求和,而根据公式 V a r [ k x ] = k 2 V a r [ x ] Var[kx]=k^2Var[x] Var[kx]=k2Var[x] ,最终会相差k^2倍。所以最后Ga的方差很大,即每次算出来的 V π ( S a ) V^\pi(S_a) Vπ(Sa)都会相差很多。
而用 TD base 中有随机性的部分是r ,它的方差比较小。但 TD 的问题在于 V π ( S t + 1 ) V^\pi(S_{t+1}) Vπ(St+1)可能不准确。
3、Q-Learning基本原理
1、另一个crtic——状态-行动价值函数 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)
与状态价值函数 V π ( s ) V^{\pi}(s) Vπ(s)的区别在于加上了动作a的影响。
状态-行动价值函数 (another critic) ) Q π ( s , a ) )Q^\pi(s, a) )Qπ(s,a)表示对于给定的actor π \pi π, 在状态s采取行动a预计能够得到的累计收益。
注意:
Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)的输入是一个 (s, a) 的 pair,然后输出一个cumulated reward的期望值。这里的cumulated reward指的是在state s下强制采取 action a(不管这个actor认为在state s下采取action a是不是好的,都强制采取a),然后用这个actor 一直玩到游戏结束所得到的cumulated reward。

以上是Q function的两种常见的写法。
如果action可以穷举,则可以使用右边的写法;否则,使用左边的写法。
2、实现步骤
1、使用一个初始的actor π \pi π 与环境进行互动学习该actor对应的 Q function
2、一定存在另外一个表现更好的actor π ′ \pi' π′, 用这个更好的acto π ′ \pi' π′r来替代原来的actor π \pi π
3、重复上述步骤
3、怎么判定 π ′ \pi' π′ 比 π \pi π好呢?
面对所有 state s 时,使用策略 π ′ \pi' π′得到的 value 一定比使用策略 π \pi π 得到的Q value 大,即 V π ′ ( s ) > V π ( s ) V^{\pi'}(s)>V^{\pi}(s) Vπ′(s)>Vπ(s)
4、如何寻找 π ′ \pi' π′ ?
找 π ′ \pi' π′ 的方法是,对于已经学到的 Q function Q π ( s , a ) Q^\pi(s,a) Qπ(s,a),在某个给定的 state 下,把每个可能的 action一一带入,看看哪一个 action 使得Q value最大,把使得函数值Q value最大的 a,作为以后面对该 state 时采取的 action。

注意:
- π ′ \pi' π′不包含额外的参数,它只取决于Q
- 对于连续的action不适用
5、证明 V π ′ ( s ) > V π ( s ) V^{\pi'}(s)>V^{\pi}(s) Vπ′(s)>Vπ(s)是存在的
4、Q-learning的三个使用技巧
1、Target network
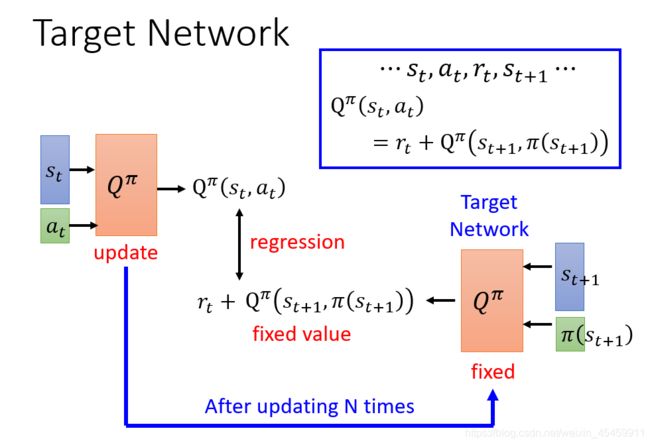
计算Q的方式与TD类似,但是在训练的过程中,由 s t s_t st和 s t + 1 s_{t+1} st+1生成的值是不固定的,在这种情况下训练会比较困难。
因此,在训练的时候,用来计算的网络会被固定 s t + 1 s_{t+1} st+1,称为固定网络,于是,目标问题就变成了一个回归问题。

2、Exploration
对于Q方程,它是policy的基础,这会导致actor每次都会选择具有更大Q值的行动action,因此可能有很多状态根本采不到。
举个例子
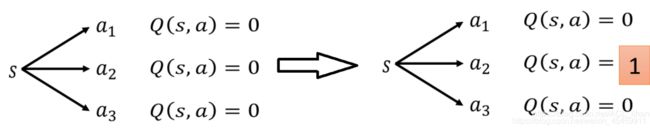
现在在状态s下,都没有采取过action a1、a2、a3,所以所有的Q-value都为0。接下来与环境的互动中,sample到在状态s下,采取动作a2,会使得Q-value从0变成1。
由 π ′ ( s ) = a r g m a x Q π ( s , a ) \pi'(s)=argmaxQ^{\pi}(s,a) π′(s)=argmaxQπ(s,a)可以知道,接下去在状态s下就会一直采取动作a2,而不会去尝试可能未来会获得更大reward的a1和a3。
可以采用两种方法来解决:
1、Epsilon Greedy

假设为0.3,那就会有0.7(1-0.3)的几率会使用以往的经验去执行动作,而剩下0.3的概率随机去试探新的动作。 ϵ \epsilon ϵ越大,探索未知动作的可能性越高,而 ϵ \epsilon ϵ会随着训练的进行不断减少。
ϵ \epsilon ϵ会随着训练的进行不断减少,就是说在一开始的时候的值会大一点,因为还不知道哪个action是好的,所以还要提高探索(exploration)的次数。随着训练的进行,开始知道哪些action是好的哪些是不好的,就可以减少探索(exploration)的次数。
2、Boltzmann Exploration
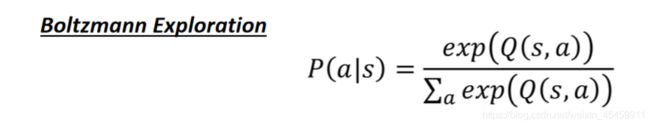
因为Q-value可能有正有负,所以先取exp全部转成正的。然后除以分母,做Normalization。
这样就将所有动作的Q value转化为概率,概率的大小和Q value的大小有关。然后通过概率的大小去选择不同动作a,概率大的被选到的次数就会多,概率小的被选到的次数就会少,这样即便Q value小的action也还是有可能会被选到。
3、Replay Buffer
把actor的每笔experience (st,at,rt,st+1)放到一个buffer里面,其中buffer里面的exp可能来自采取不同policy的actor(假设actor和环境互动一万次后就更新参数,而buffer里面能存放5万个的exp,就会导致buffer里有5种不同的actor的exp),当buffer满了再替换旧的exp。训练过程时每次从buffer里面sample一个batch(比如说100个exp)出来训练。

因为buffer里有采取不同policy的actor的experience,所以导致这个训练过程变成off-policy的。但是因为我们只用一个experience训练,并不是整个trajectory,所以off-policy也没关系。
为什么要这么做呢?
1、训练过程中与环境交互很耗时间,而Replay Buffer可以使得之前的actor的exp被反复利用到,减少了互动次数;
2、增加数据多样性,降低batch内相关性,提高泛化性能,训练效果更好。
5、经典Q-learning实现流程
参考:
https://blog.csdn.net/cindy_1102/article/details/87907470
https://blog.csdn.net/ACL_lihan/article/details/104041905




