2016年湖南省第十二届大学生计算机程序设计竞赛 解题报告

这次省赛居然出题方居然不是刘汝佳而是换成了叉姐，现场上看到ICPCCAMP这几个字的时候我的内心是血崩的/(ㄒoㄒ)/~~。不过说实话，叉姐的题，有毒!，吸的我根本停不下来~

先发个做题地址：题目

再放一个大牛的一句话题解：别人的题解

反正题面大部分都是中文，我就不描述题意了（葛优躺）

Problem A: 2016

解法1：对于一个数a，可以表示成（a/2016*2016+a%2016）的形式，那么a和b相乘是否为2016的倍数只需看右边模的部分。于是只需把所有模数的个数算出来就ok了，复杂度：2016^2。

解法2：在现场写的解法，假设我知道了一个数a，那么与a相乘能为2016的倍数的b的个数为m/(2016/gcd(a,2016))。显然枚举a是不现实的，那么我们可以尝试取枚举gcd(a,2016)=k，然后看能满足的a有多少个，由于k的枚举量不超过2016，可行，那么如何求gcd(a,2016)=k的合法数呢。假如k=1的时候，相当于求n以内有多少个数与2016互素，这个容斥一下便能解决。然后对于gcd(a,2016)=2的合法数，等价于求gcd(a/2,2016/2)=1，即n/2以内与1008互素的个数，其余同理。然后我们就求出了gcd(a,2016)=k的a的个数，乘上对应的b的个数，枚举k并累加起来便是答案。复杂度：非常快

Problem B:有向无环图
观察式子count(i,j)*a[i]*b[j]，对于一个点j来说，对答案的贡献可以表示成（∑count(i,j)*a[i]）*b[j]。动手画一画可以发现（∑count(i,j)*a[i]）是具有传递性和累加性的。我们令dp[u]表示u点上的（∑count(i,u)*a[i]），那么u点对于答案的贡献为dp[u]*b[u]，对于一个u连接的点v，dp[u]对dp[v]的贡献为dp[u]+a[u]。然后对着图的拓扑序进行dp即可

Problem C:Three Capitals

解法1：从1号点出发，遍历每条边一次后回到1号点，人们称之为欧拉回路，那么这题实际上就是欧拉回路计数了，这个时候有个名为BEST theorem的定理可以求得。该定理表示一个有向图的欧拉回路数其中tw(G)=以w为根的树形图的个数，deg(v)为点v的出度数，其中tw(G)在一般情况下需要matrix-tree定理求得，不过这题的顶点只有3个，以1为根的树形图的数目手算都能算出来所以不需要matrix-tree定理（树形图是指在图上选择一些边使图上所有节点形成一颗树，不同的边组成的树形图也算不同）。由于BEST定理是有向图的，根据欧拉回路的性质，每个顶点的出度=入度，我们可以枚举从1号点指向2号点的边数量，从而给整张图定向。最后我们把所有的欧拉回路算出来后乘上点1的出度数便是答案。

这里为何要乘上1的出度呢，要注意欧拉回路是无始无终的，以下图为例

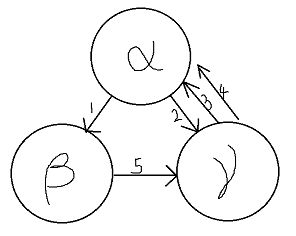
可以看到下面两种边走的方式1->5->3->2->4和2->3->4->1->5是同属于一种欧拉回路的，所以对于每一种欧拉回路我们有deg(1)种不同方式

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

解法2：BEST定理毕竟不是很多人都知道的，叉姐固然考虑到了这点，表示此题不需要BEST定理也能做，可惜在下智商做鸡，目前还没想到(T_T)

Problem D:Toll

这题有个积分号，估计吓到了不少人，不过说实话真不算难，而且各种体位都能过。

解法1：比较标准的解法，要利用到simpson积分。首先可以看到，对于每一条路径都对应了一对参数(c,d)，那么答案就是一下阴影部分面积

                                                                                                   

由于simpson积分对于次数不超过二的多项式能求出精确解，而且只需要左右端点和中点的函数值就可以求出积分值，考虑分治，对于一个区间，计算这个区间的积分值与左右两半的积分值的和，若相等，则说明这段区间是条直线，直接累加到答案上，若不相等，则继续分治下去。至于一个时间t的函数值，跑个最短路即可。

参考叉姐代码：点击打开链接

解法2：我的解法跟上面差不多，不过是从二分角度考虑。对于每一个位置t，我用二分求出这条线所能走到的位置，积分后累加到答案上

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
 >que;
    fill(dis, dis + n + 1, 1e20);
    dis[s] = 0;
    cs[s] = PII(0, 0);
    que.push(P(0, s));
     
    while (!que.empty()) {
        P p = que.top(); que.pop();
        int v = p.second;
        if (dis[v] < p.first) continue;
         
        for (int i = 0; i < g[v].size(); i++) {
            edge e = g[v][i];
            if (dis[e.to] > dis[v] + e.c * t + e.d) {
                dis[e.to] = dis[v] + e.c * t + e.d;
                cs[e.to] = PII(cs[v].fi + e.c, cs[v].se + e.d);
                que.push(P(dis[e.to], e.to));
            }
        }
    }
     
    //printf("%f %f %d %d\n", dis[n], t, cs[n].fi, cs[n].se);
    return cs[n];
}
 
double simpson(double a, double b, int c, int d) {
    return (b - a) / 6 * (c * a + d + 4 * (c * ((a + b) / 2) + d) + c * b + d);
}
 
int main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
#endif
     
     
    while (~scanf("%d%d%d", &n, &m, &T)) {
        for (int i = 0; i <= n; i++) g[i].clear();
         
        for (int i = 0; i < m; ++i) {
            int u, v, c, d;
            scanf("%d%d%d%d", &u, &v, &c, &d);
            g[u].push_back((edge) {v, c, d});
        }
         
        double ans = 0;
        double curT = 0;
        PII cd = PII(0, 0);
         
        while (curT < T) {
            double l = curT, r = T + 1;
            PII auxcd=cd;
             
            while (r - l > eps) {
                double mid = (l + r) / 2;
                PII midcd = dijkstra(1, mid);
                 
                if (midcd.fi == cd.fi && midcd.se == cd.se) l = mid;
                else {
                    r = mid;
                    auxcd = midcd;
                }
                 
            }
            if (r > T) r = T;
             
            //printf("%f ", r);
            ans += simpson(curT, r, cd.fi, cd.se);
            curT = r;
            cd = auxcd;
        }
         
        printf("%.8f\n", ans / T);
    }
}

Problem E:最长上升子序列~

原以为是dp，结果硬生生的变成了大模拟/(ㄒoㄒ)/~~

最后要求最长上升子序列的长度要恰好等于(n-1)，可以想象到其样子：在一个完全升序的串取其中一个数K放到其他地方去，其余保持升序，这样就变成了长度恰好为(n-1)的串了。由于某些位置上的值已给定，那么这时候就需要对于每一个"非0的值"进行分类讨论：

1、若所有的a[i]==i，即每个值都在他对应的位置上，对于一段连续的0的区间，若K在这里面，那么一共有(区间长度-1)^2种方法使其变成上升子序列为(n-1)的串，把每个连续的0区间累加起来便是答案。

2、若max( abs(a[i]-1) )==1，即所有的值最多偏移一位的时候，若存在两种偏移方向（即a[i]==i-1和a[i]==i+1同时存在），那么当且仅当这两个值相邻，其余非零值在原位上，答案为1，否则为0。 若只有一种偏移方向，那么不在原位上的值应该是连续的，那么答案为ans（这个自己算算把，好难表达。。。）

3、若max( abs(a[i]-1 )>=2，若存在多个偏移量大于1的值，答案为0；若只有一个，那么在那个值的原位和现在的位置中间的值应该都相应的偏移1位，其余部分的值应该在原位，若满足，答案为1，若不满足，答案为0；

注意上述的值都只算非0的，对于0直接无视。

总之好麻烦，各种分支各种细节。。。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

Problem F:地铁

这题相当有意思，解题思路完完全全就跟搭地铁一样。把每个点拆成多个点，每个新点对应一条地铁线路，换乘的花费就转换成了新点与新点上的边的花费，画个图秒懂：

                                                         

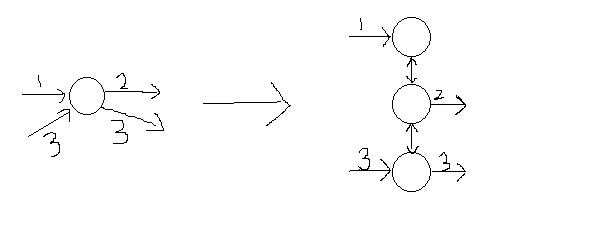
上面的1，2，3是指线路

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

Problem G:Parenthesis

水题，把'('看成1，把')'看成-1，那么这个串合法当且仅当所有的前缀和为非负整数。然后交换的时候若左边是'('右边是')'，则会使该区间内所有前缀和减2，所以在这种情况下看该区间的最小值是否>=2即可。其余交换方式直接'yes'

Problem H:Reverse

数学公式推导题。每个d[i]对最后答案的贡献分两种，一种是交换区间(l,r)不包含i，这种好算；另一种(l,r)包含i，这个时候我们可以找到这么个规律，当我们固定r，枚举l的时候，对于所有包含i的区间，d[i]能交换到的位置是已r为右边界，长度为i的连续区间，然后提提公因数，算算等比数列等差数列答案就出来了。

Problem I:Tree Intersection

还是先转一个别人的题解：点击打开链接

这位大牛已经说的很好了，dfs序是个好东西，他往往能将树转换成数列，然后在数列上进行操作。

同时这题还能用启发式合并去做，先转一个ICPCCAMP里对启发式合并的讨论：点击打开链接

这可真是个神奇的东西，只需要每次合并的时候把小的集合合并到大的集合，时间复杂度就能神奇的变成nlogn。

由于上面大牛的启发式合并用的是主席树和splay树，作为一个弱逼并不太会，只好用map来进行启发式合并，效率大概比主席树慢了6倍左右

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

Problem J:三角形和矩形

完全不会计算几何，已机智的扔给队友。水题，各种体位都能过。

Problem K:盖房子

像这种考虑两个东西组合的时候，我们往往需要先考虑只需要盖一个房子的时候。那么这样问题就变成了在这么个有障碍的地图上有多少个合法矩形，刘汝佳紫书上有个类似的问题，我们可以利用单调栈求得对于每个位置，以他为左上，左下，右上，右下角的时候的合法矩形数，然后我们现在需要利用这些信息去求两个不相交的矩形方案数。

以点(i,j)为右下角画矩形，为了保证不相交我们只能在除去(1,1)到(i,j)矩形上的其余位置当左上角做矩形，把两者数量相乘。然后发现，大部分矩形对都只算了一次，唯有一个矩形完全在另一个矩形的右上方或完全在左下方的时候重算了一次。所以这个时候我们只需要减去这种情况即可。表达不清，详见代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

总的来说，叉姐的题目质量还是非常高的，学习价值很大，A上一遍很有必要( •̀ ω •́ )y