堆排序详解（升序和降序Java版本）

一、概述

1.堆排序的思路主要就是建堆和排序两部分组成。堆排序是基于二叉树的，那么我们首先得知道二叉树得基本特性。我们在堆排序中定义这样一种完整二叉树，其中每个结点的值都大于等于它的孩子，那么我们就称之为最大堆，同理还有最小堆。接下来重要的是我们在建立完最大堆之后，我们需要再次进行上浮或者下沉操作，使得二叉树仍然满足最大对的定义。

2.二叉树概述

二叉树得结点一般用于存储我们要处理的数据，而结点位置可以通过编号给出简单且唯一的描述：

• 结点编号一般取整数，我们称树中编号为k的结点为结点k
• 一棵非空二叉树根结点的编号为1，这是最小的编号
• 结点k的左孩子和右孩子编号分别为2k和2k+1,而节点k称为这两个孩子的父亲

   按照上述规则，可知结点k的父亲结点编号为k/2。另外二叉树的层次也很重要，一般定义根节点 处于第0层，以此为基础不断递增，也即所有位于第L层的结点其孩子所在层次为L+1。二叉树的高度定义为该树中结点的最大层数，若二叉树是一颗结点总数为2^(h+1)-1的完整二叉树（h为二叉树的高度），那么称该二叉树为完美二叉树。
   二叉树中结点的的孩子数称为该节点的度，显然度为0的结点称为叶子结点，否则称为非叶子结点。若二叉树中非叶子结点的度均为2，那么就称该二叉树为满二叉树

3.总结

• 非空二叉树的第i层最多有2^i个结点
• 高为h的非空二叉树最多包含的结点数为2^(h+1)-1个
• 设i = 0,1,2 ,若非空二叉树中度为i的结点数为Ni，则N0 = N2 + 1

二、建堆算法

这里我在课本上学习的建堆方法有两种，分别是Williams建堆法和Floyd建堆法，接下来将讲述这两种建堆方法的区别，在一般的堆排序中我们建议使用Floyd建堆法，因为它的时间复杂度更低并且代码更加容易实现。但是还是要将每种的实现步骤画一遍。

1.Williams算法建堆法【Wil64】

时间复杂度为O(nlogn),空间为O(1)
例如我们对数组[4,7,5,8,6,0,2,3,9,1]进行从小到大排列，因为我们是要从小到达进行排列所以我们应该建立最大堆。
我们知道在建立完最大堆之后，就要开始进行弹出操作，我们最先弹出的数字永远放在最后面因此从小到大的排列就需要建立最大堆。

这是我们要排序的数组。

开始建堆
第一步

第二步（因为7比4大所以交换顺序）

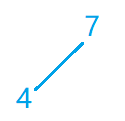
第三步（5比父节点小，所以当作6的右孩子就可以）

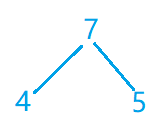
第四步

第五步

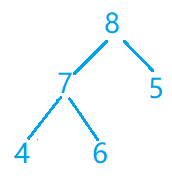
第六步

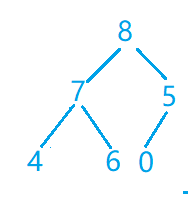
第七步

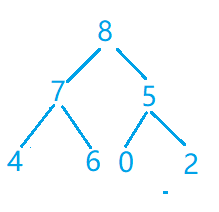
第八步

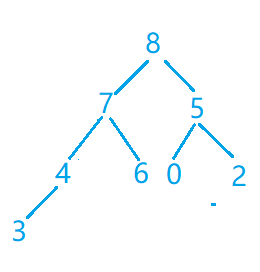
第九步

第十步

到这里我们就建完了我们的最大堆，
接下来我们就开始进行弹出操作：
首先走到这里我们一斤建好了我们的最大堆，我们现在就开始进行弹出操作，也就是我们的排序。
第一步（弹出9）

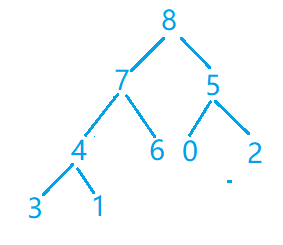
第二步（弹出8）

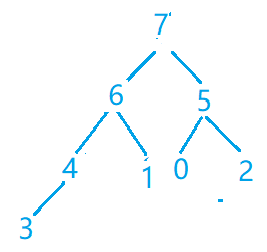
第三步（弹出7）

第四步（弹出6）

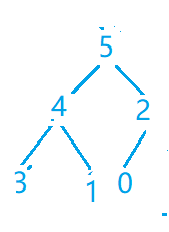
第五步（弹出5）

第六步（弹出4）

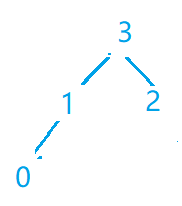
第七步（弹出3）

第八步（弹出2）

第九步（弹出1）

第十步（弹出0）
这里我们就已经排序完成，我们首先弹出来的在后面

2.Floyd算法建堆法【Floo64】

一种更为高效的建堆方法，可以在O(时间)和O(1)空间内完成建堆任务。
他的要点就是从最后一个非叶子结点从后向前对那些有孩子的结点执行下沉操作 ，从而来建立我们的最大堆。在开始之前还是要强调要会计算某个结点的左右孩子结点，和孩子节点的父结点。

最开始的数组

建堆
第一步（最开始的堆）
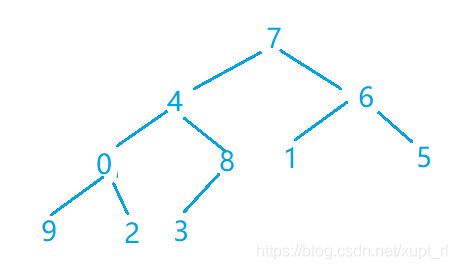第二步（元素8无需调整，因为以它为根的子树已经是子堆）

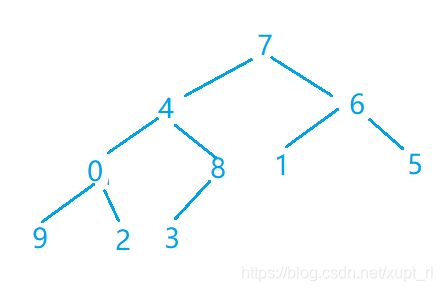
第三步（元素0下沉后原位置对应一个以9为对顶的子堆）
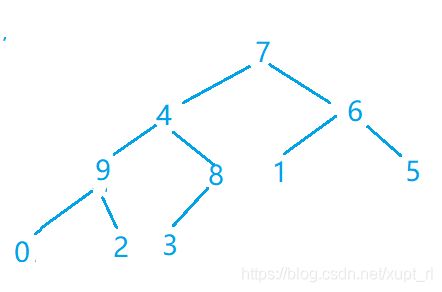第四步（元素6无需调整，因为以它为根的子树已经是子堆）

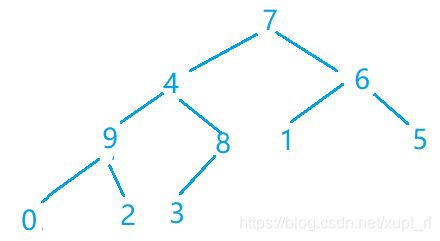
第五步（元素4下沉后原位置对应一个以9为对顶的子堆）
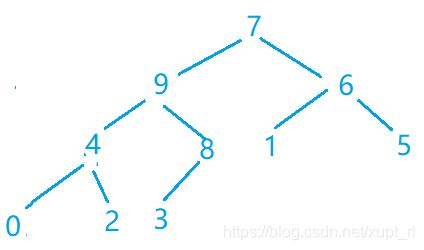第六步（元素7下沉后原位置（已经是根节点）对应一个以9为对顶的子堆）
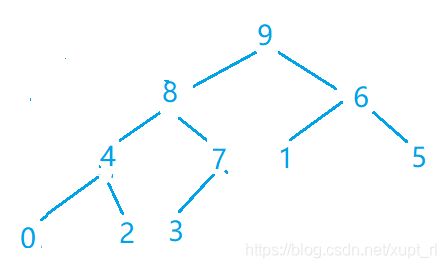到这里我们就已经完成建堆任务，这里有一个定义Floyd算法可以在O(n)时间内完成对n个元素建堆的任务。
后面的就和上一个弹出操作类似，这里就不展示每一次步骤了。

三、基于Floyd建堆算法进行堆排序

1.最小堆
在开始之前我们前面已经知道了怎样表示一个结点的左孩子和右孩子，以及知道某个结点可以求出其父亲结点。先下面我们对数组进行从大到小排序，因此我么应该建立最小堆。

package org.westos.demo;



import java.util.Arrays;
import java.util.Scanner;

public class HeapSort3 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.println("请输入你要排序的数字的个数");
        int n = sc.nextInt();
        int[] tree = new int[n];
        for (int i = 0; i < tree.length; i++) {
            tree[i] = sc.nextInt();
        }
        heap_sort(tree,tree.length);
        System.out.println(Arrays.toString(tree));
    }
    //我们在建好堆的基础之上，进行排序，每次排完序之后要记得重新进行下沉操作，从而使得堆满足最大（小）堆的特性
    public static void heap_sort(int[]tree,int n){
        build_heap(tree,n);
        for (int i = n-1; i >= 0; i--) {
            swap(tree,i,0);
            heapify(tree,i,0);
        }
    }

    /**
     *
     * @param tree 要排序的数组
     * @param n    数组的长度
     * 从最后一个非叶子结点从后向前进行建堆，这里我们使用的是Floyd建堆算法
     */
    public static void build_heap(int[]tree,int n){
        int last_node = n - 1;
        int parent = (last_node - 1)/2;
        for (int i = parent;i >= 0;i--){
            heapify(tree,n,i);
        }
    }

    /**
     *
     * @param tree 要排序的数组
     * @param n    数组的长度
     * @param i    表示第i个节点
     * 这里我们对元素进行下沉操作
     */
    public static void heapify(int[]tree,int n,int i){
        if(i >= n){
            return;
        }
        int c1 = 2 * i +1;//左孩子结点
        int c2 = 2 * i +2;//右孩子结点
        int max = i;//父亲结点
        //下面就是判断父亲结点和孩子结点的大小，从而进行下沉操作
        if (c1 < n && tree[max] > tree[c1]){//这里得加上c1 < n 防止越界
            max = c1;
        }
        if (c2 < n && tree[max] > tree[c2]){//这里得加上c2 < n 防止越界
            max = c2;
        }
        if (max != i){
            swap(tree,max, i);
            heapify(tree,n,max);
        }
    }
    public static void swap(int[]tree,int i,int j){
        int temp = tree[i];
        tree[i] = tree[j];
        tree[j] = temp;
    }
}

验证

请输入你要排序的数字的个数
10
7
4
6
0
8
1
5
9
2
3
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]

Process finished with exit code 0

2.最大堆
这里我们只需要在上面代码出改变一处位置就OK，就是我们在进行下沉操作的时候，判断父亲结点与孩子结点的值的大小就可以。

package org.westos.demo;



import java.util.Arrays;
import java.util.Scanner;

public class HeapSort3 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.println("请输入你要排序的数字的个数");
        int n = sc.nextInt();
        int[] tree = new int[n];
        for (int i = 0; i < tree.length; i++) {
            tree[i] = sc.nextInt();
        }
        heap_sort(tree,tree.length);
        System.out.println(Arrays.toString(tree));
    }
    //我们在建好堆的基础之上，进行排序，每次排完序之后要记得重新进行下沉操作，从而使得堆满足最大（小）堆的特性
    public static void heap_sort(int[]tree,int n){
        build_heap(tree,n);
        for (int i = n-1; i >= 0; i--) {
            swap(tree,i,0);
            heapify(tree,i,0);
        }
    }

    /**
     *
     * @param tree 要排序的数组
     * @param n    数组的长度
     * 从最后一个非叶子结点从后向前进行建堆，这里我们使用的是Floyd建堆算法
     */
    public static void build_heap(int[]tree,int n){
        int last_node = n - 1;
        int parent = (last_node - 1)/2;
        for (int i = parent;i >= 0;i--){
            heapify(tree,n,i);
        }
    }

    /**
     *
     * @param tree 要排序的数组
     * @param n    数组的长度
     * @param i    表示第i个节点
     * 这里我们对元素进行下沉操作
     */
    public static void heapify(int[]tree,int n,int i){
        if(i >= n){
            return;
        }
        int c1 = 2 * i +1;//左孩子结点
        int c2 = 2 * i +2;//右孩子结点
        int max = i;//父亲结点
        //下面就是判断父亲结点和孩子结点的大小，从而进行下沉操作
        if (c1 < n && tree[max] < tree[c1]){//这里得加上c1 < n 防止越界
            max = c1;
        }
        if (c2 < n && tree[max] < tree[c2]){//这里得加上c2 < n 防止越界
            max = c2;
        }
        if (max != i){
            swap(tree,max, i);
            heapify(tree,n,max);
        }
    }
    public static void swap(int[]tree,int i,int j){
        int temp = tree[i];
        tree[i] = tree[j];
        tree[j] = temp;
    }
}

测试：

请输入你要排序的数字的个数
10
7
4
6
0
8
1
5
9
2
3
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Process finished with exit code 0

四、总结

在刚开始学完堆排序之后，我只是简单的懂了其中的原理，但是当我真正用代码进行实现的时候，才发现自己遇见了很大的问题，虽然每一步的流程图都可以画出来，但是代码还是不知道怎么实现。首先堆排序利用了二叉树，那么首先就要对二叉树了解，另外还有里面的相关结点的计算，接下来就是按照每一步的流程用代码实现，这里面还有好几处边界问题也应该注意，另外，如果不知道思路大概画一遍就可以更加深入的了解其中的原理。