【学习笔记】Pytorch深度学习—损失函数(二)
【学习笔记】Pytorch深度学习—损失函数(二)
- 5、nn.L1Loss
- 6、nn.MSELoss
- 7、nn.SmoothL1Loss
- 8、nn.PoissonNLLLoss
- 9、nn.KLDivLoss
- 10、nn.MarginRankingLoss
- 11、nn.MultilabelMarginLoss
- 12、nn.SoftMarginLoss
- 13、nn.MultiLabelSoftMarginLoss
- 14、nn.MultiMarginLoss
- 15、nn.TripletMarginLoss
- 16、nn.HingeEmbeddingLoss
- 17、nn.CosineEmbeddingLoss
- 18、nn.CTCLoss
5、nn.L1Loss
回归任务中常用的损失函数。
功能:计算模型输出inputs与真实标签target之差的绝对值
L n = ∣ x n − y n ∣ L_n=\vert x_n-y_n\vert Ln=∣xn−yn∣
6、nn.MSELoss
回归任务中常用的损失函数。
功能:计算模型输出inputs与target之差的平方
L n = ( x n − y n ) 2 L_n=( x_n-y_n)^2 Ln=(xn−yn)2
nn.L1Loss(size_average=None,reduce=None,reduction='mean')
nn.MSELoss(size_average=None,reduce=None,reduction='mean')
reduction:计算模式,可为none(逐个元素计算)/sum(所有元素求和,返回标量)/mean(加权平均,返回标量)
实验
(1)L1Loss:计算模型输出与target之差的绝对值
(2)MSELoss:计算模型输出与target之差的平方
注意事项:reduction采用none模式,以每个神经元一一对应计算L1Loss和MSELoss。
//创建输入为2*2张量,值全为1。target同样大小的张量,元素值为3.
inputs = torch.ones((2, 2))
target = torch.ones((2, 2)) * 3
loss_f = nn.L1Loss(reduction='none')
loss = loss_f(inputs, target)
print("input:{}\ntarget:{}\nL1 loss:{}".format(inputs, target, loss))
# ------------------------------------------------- 6 MSE loss ----------------------------------------------
loss_f_mse = nn.MSELoss(reduction='none')
loss_mse = loss_f_mse(inputs, target)
print("MSE loss:{}".format(loss_mse))
实验结果:

7、nn.SmoothL1Loss
功能:平滑的L1Loss
L o s s ( x , y ) = 1 n ∑ i Z i Loss(x,y)=\frac{1}{n}\sum_i{Z_i} Loss(x,y)=n1i∑Zi
Z i Z_i Zi是如何求解的? Z i Z_i Zi是分段函数;其中, x i x_i xi是模型输出, y i y_i yi是真实标签。
Z i = { 0.5 ( x i − y i ) 2 , i f ∣ x i − y i ∣ < 1 ∣ x i − y i ∣ − 0.5 , o t h e r w i s e \ Z_i = \begin{cases} 0.5(x_i-y_i)^2, & if\vert x_i-y_i\vert < 1 \\\vert x_i-y_i\vert-0.5, & otherwise \end{cases} Zi={0.5(xi−yi)2,∣xi−yi∣−0.5,if∣xi−yi∣<1otherwise

实验
结合图2的实验结果可以看出,相对于L1Loss损失函数,SmoothL1Loss通过"这一平滑"可以减轻离群点带来的影响。
//构建inputs模型输出,对应于公式中的 x,在[-3,3]上平均的取500个数据点
inputs = torch.linspace(-3, 3, steps=500)
//构建与 inputs模型输出 同维度的标签target,元素为0
target = torch.zeros_like(inputs)
//采用none一一对应求解Loss
loss_f = nn.SmoothL1Loss(reduction='none')
loss_smooth = loss_f(inputs, target)
loss_l1 = np.abs(inputs.numpy())
plt.plot(inputs.numpy(), loss_smooth.numpy(), label='Smooth L1 Loss')
plt.plot(inputs.numpy(), loss_l1, label='L1 loss')
plt.xlabel('x_i - y_i')
plt.ylabel('loss value')
plt.legend()
plt.grid()
plt.show()
8、nn.PoissonNLLLoss
功能:泊松分布的负对数似然损失函数
输出分类时,分类服从泊松分布时采用的损失函数。
nn.PoissonNLLLoss(log_input=True,
full=False,
size_average=None,
eps=1e-08,
reduce=None,
reduction='mean')
(1)log_input=True,
loss(input,target)=exp(input)-target*input;
(2)log_input=False,
loss(input,target)=input-target*log(input+eps)
主要参数:
log_input:输入是否为对数形式,决定计算公式
full:计算所有Loss,默认为False
eps:修正项,避免log(input)为nan
解释:
(1)log_input:指示输入数据是否已经为对数形式,直接决定了计算公式形式;
① log_input=True,
loss(input,target)=exp(input)-target * input ;
如果log_input=False:输入数据还不是对数形式,计算中还需要对input取对数,取对数时有可能遇到input=0,这样就无法正常进行取对数运算,因此在input后加入修正项eps。其中修正项很小,大概在 1 0 − 8 10^{-8} 10−8,它的加入并不会影响到对input对数数值的,即便有影响也可忽略不计。
② log_input=False,
loss(input,target)=input-target * log(input+eps)
(2)eps:修正项,将eps加在input后构成log(input+eps),从而避免nan现象。
实验—当默认模式log_input=True,泊松分布负对数似然函数nn.PoissonNLLLoss的使用方法和计算
//输入和标签都在正态分布中以随机采样的方式获取2×2张量
inputs = torch.randn((2, 2))
target = torch.randn((2, 2))
loss_f = nn.PoissonNLLLoss(log_input=True, full=False, reduction='none')
loss = loss_f(inputs, target)
print("input:{}\ntarget:{}\nPoisson NLL loss:{}".format(inputs, target, loss))
9、nn.KLDivLoss
功能:相对熵损失函数也称KLD(divergence)、KL散度
注意事项:
需提前将输入计算log-probabilities,如通过nn.logsoftmax()实现
nn.PoissonNLLLoss(size_average=None,
reduce=None,
reduction='mean')
主要参数:
reduction:none/sum/mean/batchmean(以batchsize维度求平均值)
由于相对熵损失函数(KL散度)衡量的是2个概率分布之间的差异,用来计算2个概率分布的距离。因此,应当保证参与计算的输入应当在概率区间,并且Pytorch提供的KLDivLoss计算公式也是直接取输入(模型输出值 x n x_n xn)计算,因而利用该函数计算应当提前计算log-probabilities,如通过nn.softmax()实现。

实验
//该输入处于概率区间(0,1),符合probabilities
inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
//预先进行log计算
inputs_log = torch.log(inputs)
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)
loss_f_none = nn.KLDivLoss(reduction='none')
loss_f_mean = nn.KLDivLoss(reduction='mean')
loss_f_bs_mean = nn.KLDivLoss(reduction='batchmean')
loss_none = loss_f_none(inputs, target)
loss_mean = loss_f_mean(inputs, target)
loss_bs_mean = loss_f_bs_mean(inputs, target)
10、nn.MarginRankingLoss
功能:计算两个向量之间的相似度,用于排序任务
特别说明:该方法计算两组数据之间的差异,返回1个n*n的Loss矩阵。
nn.MarginRankingLoss(margin=0.0,
size_average=None,
reduce=None,
reduction='mean')
主要参数:
margin:边界值,x1与x2之间的差异值
reduction:计算模式none/sum/mean

实验
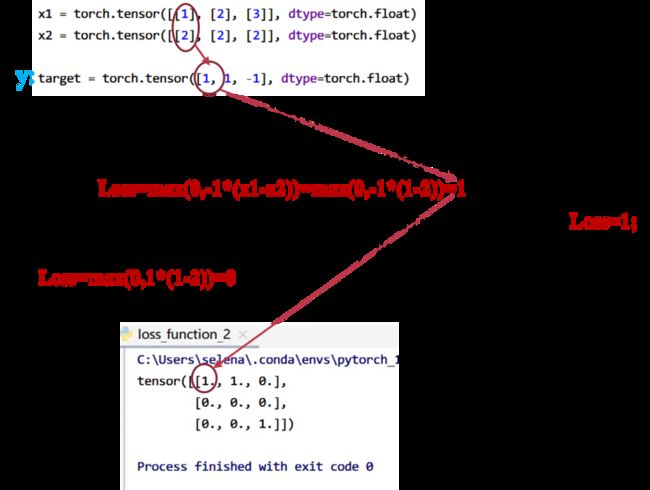
x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)
target = torch.tensor([1, 1, -1], dtype=torch.float)
loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')
loss = loss_f_none(x1, x2, target)
print(loss)
实验结果
11、nn.MultilabelMarginLoss
功能:多标签边界损失函数
容易将多标签与多分类任务混淆。
多标签是指一个样本可能对应多个类别。一些任务会将图像进行分类,即风景、人像、美食进行基本划分,这时会对图像基本元素进行分类,比如下述图6风景图像有云、树、草地等标签,因此这张图片可能对应多个类别。

nn.MarginRankingLoss(size_average=None,
reduce=None,
reduction='mean')
主要参数:
reduction:计算模式none/sum/mean
举例:四分类任务,样本x属于0类和3类,标签:[0,3,-1,1]而非~~[1,0,0,1]~~

12、nn.SoftMarginLoss
功能:计算二分类的logistic损失
L o s s ( x , y ) = ∑ i l o g ( 1 + e x p ( − y [ i ] ∗ x [ i ] ) ) x . n e l e m e n t ( ) \ Loss(x,y) = \sum_i \frac{log(1+exp(-y[i]*x[i]))}{x.nelement()} Loss(x,y)=i∑x.nelement()log(1+exp(−y[i]∗x[i]))
nn.SoftMarginLoss(size_average=None,
reduce=None,
reduction='mean')
主要参数:
weight:各类别的Loss设置权值
reduction:计算模式none/sum/mean
13、nn.MultiLabelSoftMarginLoss
MultiLabelSoftMarginLoss第12个损失函数的多标签版本
功能:SoftMarginLoss的多标签版本
nn.SoftMarginLoss(weight=None,size_average=None,
reduce=None,
reduction='mean')
主要参数:
reduction:计算模式none/sum/mean

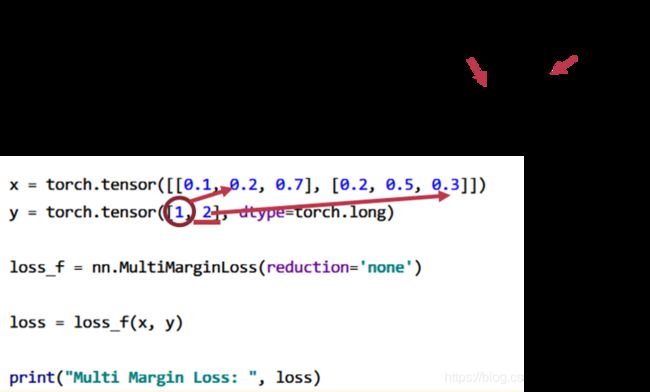
14、nn.MultiMarginLoss
功能:计算多分类的折页损失
nn.MultiMarginLoss(p=1,margin=1.0,weight=None,
size_average=None,
reduce=None,
reduction='mean')
主要参数:
p:可选1或2
weight:各类别的loss设置权值
margin:边界值
reduction:计算模式none/sum/mean
15、nn.TripletMarginLoss
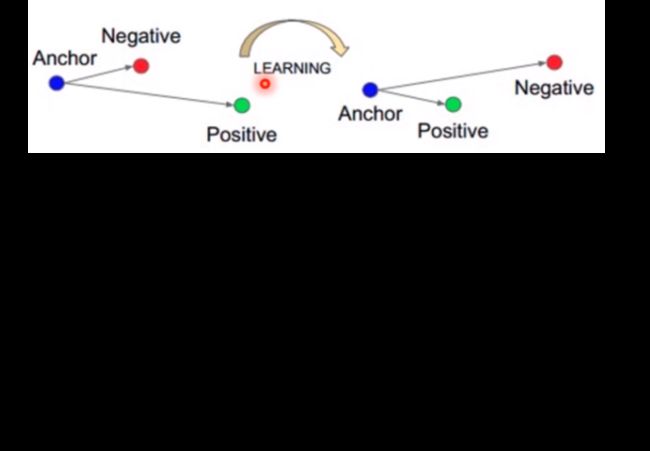
功能:计算三元组损失,人脸验证中常用。
通过学习,希望Anchor与Negative之间的距离要更长,Anchor与Positive之间的距离更短。
nn.TripletMarginLoss(margin=1.0,p=2.0,eps=1e-06,
swap=False,
size_average=None,
reduce=None,
reduction='mean')
主要参数:
p:范数的阶,默认为2
margin:边界值
reduction:计算模式none/sum/mean
人脸验证中经常使用,Anchor是自己人脸图像,Positive自己的人脸图像,Negative是其他人的人脸图像,训练时希望自己的人脸图像相近,而与其他人的人脸图像不相同。
16、nn.HingeEmbeddingLoss
功能:计算两个输入的相似性,常用于非线性embedding(嵌入学习)和半监督学习
nn.HingeEmbeddingLoss(margin=1.0,
size_average=None,
reduce=None,
reduction='mean')
主要参数:
margin:边界值
reduction:计算模式none/sum/mean

17、nn.CosineEmbeddingLoss
功能:采用余弦相似度计算两个输入的相似性
nn.CosineEmbeddingLoss(margin=0.0,
size_average=None,
reduce=None,
reduction='mean')
主要参数:
margin:边界值,可取值[-1,1],推荐为[0,0.5]
reduction:计算模式none/sum/mean
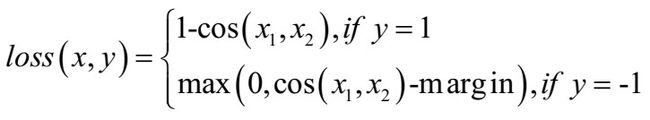
18、nn.CTCLoss
功能:计算CTC损失,解决时序类数据的分类。比如OCR中,输入和输出长度不确定的情况下,计算其分类可用到CTCLoss,通常在图像任务中使用比较少。
torch.nn.CTCLoss(blank=0.0,
reduction='mean',
zero_infinity=False)
主要参数:
blank:blank label
zero_infinity:无穷大的值或梯度置0
reduction:计算模式none/sum/mean
以上是Pytorch中18种损失函数,需要仔细整理,在具体任务中选择衡量输出与标签之间差异的相应损失函数。