深度学习基础要点和Pytorch常用命令汇总

深度学习基础

卷积

计算卷积后的图片size
$size=[\frac{l+2\ast p-k}{s}+1$]
其中：
$l=图片原尺寸$
$p=padding大笑$
$k=卷积核大小$
$s=步长$

卷积参数个数
假设输入为388，输出为655，卷积核大小为333
那么因为输出有6个channel，所以需要6个333的卷积核

对于Pytorch可以用下面代码查看参数：

for name,parameters in net.named_parameters():
	print(name,':',paramaters.size())

卷积层激活函数
激活函数一般是在每次卷积后就使用

池化

计算池化后的图片size
方法同卷积操作

---

优化算法

梯度下降法

batch梯度下降法（batch_size=样本大小）当样本数小于2000
mini_batch梯度下降法（batch_size介于之间）样本数大于2000，一般batch_size设为64～512（2的倍数）
随机梯度下降法（batch_size=1）

$W:=W-\alpha \ast dW$

动量梯度下降 Momentum梯度下降

首先理解加权指数平均

$V_0=0$
$V_1=\beta \ast V_0+(1-\beta )\ast {\theta }_1$
$V_2=\beta \ast V_1+(1-\beta )\ast {\theta }_2$
$...$
$V_n=\beta \ast V_{n-1}+(1-\beta )\ast {\theta }_n$

当β=0.9时，表示v_t平均了之前1/(1-β)即10时间的值，β值越大，v_t曲线越平滑
在前期，为了避免v_0=0这种异常值，用v_t/(1-β^t)代替v_t，这叫做偏差修正，但神经网络一般不使用
$V_{dW}:=\beta \ast V_{dW}+(1-\beta )\ast dW$
$W:=W-\alpha \ast V_{dW}$

RMSprop

$S_{dW}:=\beta \ast S_{dW}+(1-\beta )\ast d{W}^2$
$W:=W-\alpha \ast \frac{dW}{\sqrt{S_{dW}}+ϵ}$
$ϵ是极小量，为了不除以0$

Adam(Adaptive Moment Estimation)

$V_{dW}:=\beta 1\ast V_{dW}+(1-\beta 1)\ast dW$
$S_{dW}:=\beta 2\ast S_{dW}+(1-\beta 2)\ast d{W}^2$
$W:=W-\alpha \ast \frac{V_{dW}}{\sqrt{S_{dW}}+ϵ}$
$\beta 1常取0.9$
$\beta 2常取0.999$
$ϵ常取10^{-8}$

---

pytorch框架

损失函数 Loss Functions

L1Loss

class torch.nn.L1Loss(size_average=True, reduce=True)
创建一个衡量输入 x 与目标 y 之间差的绝对值的平均值的标准, 该 函数会逐元素地求出 x 和 y 之间差的绝对值, 最后返回绝对值的平均值.(在默认条件下，即size_average=True, reduce=True)

loss(x,y)=1/n∑|xi−yi|

当reduce=False时（此时size_average参数失效）
创建2*2*2矩阵，模拟batch_size=2，即每个mini_batch中有两个矩阵，每个矩阵大小2*2

v1=Variable(torch.FloatTensor([
    [[1,2],[3,4]],
    [[0,-1],[-2,0]]
]))


v2=Variable(torch.FloatTensor([
    [[2,-1],[1,3]],
    [[4,0],[-1,2]]
]))

print(v1)
#
Variable containing:
(0 ,.,.) = 
  1  2
  3  4

(1 ,.,.) = 
  0 -1
 -2  0
[torch.FloatTensor of size 2x2x2]

print(v2)
#
Variable containing:
(0 ,.,.) = 
  2 -1
  1  3

(1 ,.,.) = 
  4  0
 -1  2
[torch.FloatTensor of size 2x2x2]

然后求L1Loss

criterion=nn.L1Loss(reduce=False)
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
(0 ,.,.) = 
  1  3
  2  1

(1 ,.,.) = 
  4  1
  1  2
[torch.FloatTensor of size 2x2x2]

返回同样是2*2*2矩阵，相当于每个位置求|xi-yi|

当reduce=True size_average=False时
测试样例同上

criterion=nn.L1Loss(size_average=False)
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
 15
[torch.FloatTensor of size 1]

是把每个位置差的绝对值求和(以mini_batch为单位)

当reduce=True size_average=False时

criterion=nn.L1Loss(size_average=True)
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
 1.8750
[torch.FloatTensor of size 1]

把上面所求的和再除以mini_batch所有矩阵内元素（如上，除以8）个数

MSELoss

class torch.nn.MSELoss(size_average=True, reduce=True)
同L1Loss，只不过这是求差的绝对值的平方和的平均loss(x,y)=1/n∑|xi−yi|^2
样例仍使用上面的v1 v2

criterion=nn.MSELoss(reduce=False)
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
(0 ,.,.) = 
   1   9
   4   1

(1 ,.,.) = 
  16   1
   1   4
[torch.FloatTensor of size 2x2x2]

criterion=nn.MSELoss(size_average=False)
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
 37
[torch.FloatTensor of size 1]

criterion=nn.MSELoss()//默认参数设置
loss=criterion(v1,v2)
print(loss)
#
Variable containing:
 4.6250
[torch.FloatTensor of size 1]

NLLLoss & CrossEntropyLoss

nn.CrossEntropyLoss = nn.LogSoftmax() + nn.NLLLoss()

m=nn.LogSoftmax()
loss=nn.NLLLoss(reduce=False)
loss2=nn.CrossEntropyLoss(reduce=False)

test=Variable(torch.randn(4,3))
target=Variable(torch.LongTensor([0,2,1,1]))
output=loss(m(test),target)
output2=loss2(test,target)
print(test)
print(F.log_softmax(test))
print(output)
print(output2)
# test 源数据
Variable containing:
 0.4137 -0.4271 -0.7461
 1.5289 -1.4904  2.1758
-1.8883 -0.0124 -1.6840
-0.2659 -0.7639  0.6339
[torch.FloatTensor of size 4x3]
# F.log_softmax() 
Variable containing:
-0.5567 -1.3975 -1.7165
-1.0847 -4.1040 -0.4378
-2.1694 -0.2935 -1.9652
-1.4029 -1.9009 -0.5031
[torch.FloatTensor of size 4x3]
# nn.NLLLoss(input,target)
# input 为F.log_softmax()之后的值，target为一维数组，不是one-hot格式
Variable containing:
 0.5567
 0.4378
 0.2935
 1.9009
[torch.FloatTensor of size 4]
# nn.CrossEntropyLoss
# input 为源数据
Variable containing:
 0.5567
 0.4378
 0.2935
 1.9009
[torch.FloatTensor of size 4]

---

非线性层(函数) Non-linear Activations

F.softmax & nn.LogSoftmax() & F.log_softmax()

torch.nn.functional.softmax(input, dim=None, _stacklevel=3)
softmax(x)=exp(xi)/∑exp(xj)

data=Variable(torch.randn(4,3))
print(data)

print('F.softmax')
print(F.softmax(data))

print('log(F.softmax)')
print(np.log(F.softmax(data).data.numpy()))

print('F.log_softmax')
print(F.log_softmax(data))

m=nn.LogSoftmax()
print('nn.LogSoftmax')
print(m(data))

#
Variable containing:
 0.8420  1.0236  1.4242
-0.7329 -0.7940  0.7947
-0.3812 -0.3296 -0.0830
 0.6234 -1.7182  0.6242
[torch.FloatTensor of size 4x3]
#
F.softmax
Variable containing:
 0.2507  0.3006  0.4487
 0.1527  0.1437  0.7036
 0.2941  0.3097  0.3963
 0.4769  0.0459  0.4773
[torch.FloatTensor of size 4x3]
#
log(F.softmax)
[[-1.3836101  -1.2019439  -0.80135906]
 [-1.8791015  -1.9402403  -0.35154063]
 [-1.2239172  -1.1722705  -0.9256822 ]
 [-0.7405206  -3.0821092  -0.7396687 ]]
 #
 F.log_softmax
Variable containing:
-1.3836 -1.2019 -0.8014
-1.8791 -1.9402 -0.3515
-1.2239 -1.1723 -0.9257
-0.7405 -3.0821 -0.7397
[torch.FloatTensor of size 4x3]
#
nn.LogSoftmax
Variable containing:
-1.3836 -1.2019 -0.8014
-1.8791 -1.9402 -0.3515
-1.2239 -1.1723 -0.9257
-0.7405 -3.0821 -0.7397
[torch.FloatTensor of size 4x3]

可见，F.softmax()求出的各元素在这一行占的比例（默认dim情况下），nn.LogSoftMax()求出的等同于在F.sofgmax()后再使用log函数

F.max_pool2d

document

F.relu

document

---

torchvision

tv.transforms.ToTensor()

将范围 [0, 255] 中的 PIL Image 或 numpy.ndarray (H x W x C) 转换形状为 (C x H x W) , 值范围为 [0.0, 1.0] 的 torch.FloatTensor.

tv.transforms.Normalize()

input[channel] = (input[channel] - mean[channel]) / std[channel]

transform=transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5))
])

---

torch.nn

nn.Conv2d

torch.nn.Conv2d

nn.Linear

torch.nn.Linear

nn.Normal2d

torch.nn.Normal2d
批量归一化，和数据归一化不同，是在神经网络层中归一化

nn.Module

注意： 当神经网络有dropout和BatchNorm时，在训练前要加上net.train()，在测试时要加上net.eval()

保存和加载模型

# 保存和加载整个模型
torch.save(model_object, 'model.pkl')
model = torch.load('model.pkl')

# 仅保存和加载模型参数(推荐使用)
torch.save(model_object.state_dict(), 'params.pkl')
model_object.load_state_dict(torch.load('params.pkl'))

---

array numpy tensor Variable格式互转

array 转 numpy

arr_data=[1,2,3,4]
np_data=np.array(arr_data)

numpy 转 array

arr_data2=[np_data]

array 转 tensor

tensor=torch.FloatTensor(array)

numpy 转 tensor

tensor=torch.from_numpy(np_data)

tensor 转 numpy

data=tensor.numpy()

tensor 转 Variable

variable=Variable(tensor)

Variable 得 tensor

tensor_data=variable.data

Variable 得 numpy

numpy_data=variable.data.numpy()

torch维度

tensor.size()

Variable的梯度grad属性

v_out=torch.mean(variable*variable)
v_out.backward()
print(variable.grad)
//输出[[0.5,1],[1.5,2]]

矩阵相乘

mat_data=torch.FloatTensor([[1,2],[3,4]])
print(torch.mm(mat_data,mat_data)) 
//输出 [[7,10],[15,22]]

mat_data_flat=torch.FloatTensor([1,2,3,4])
print(mat_data_flat.dot(mat_data_flat.dot(mat_data_flat)))
// 输出 30.0

数学运算

平均值

mat_data=torch.FloatTensor([[1,2],[3,4]])
mat_mean=torch.mean(mat_data)
//输出2.5

直接相乘

mat_data=torch.FloatTensor([[1,2],[3,4]])
print(mat_data*mat_data)
// 输出 [[1,4],[9,16]]

正弦函数

torch.sin()

随机数

torch.rand(10)
# 10个0-1均匀分布

均匀数列

x=torch.linspace(-1,1,10)

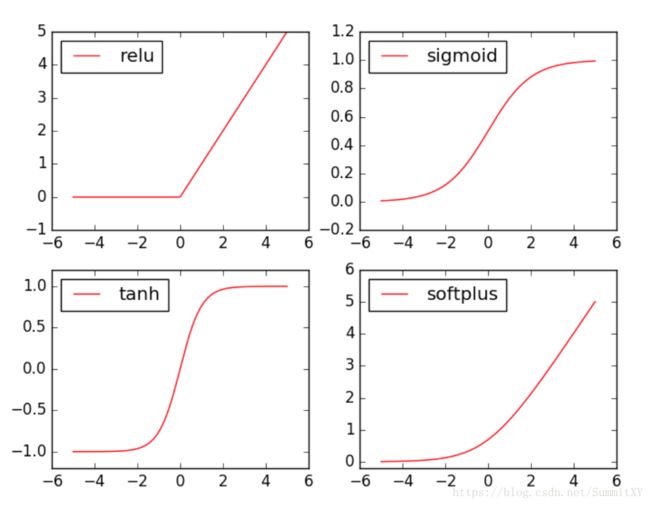
激活函数

matplotlib

pyplot只能处理numpy格式数据

画曲线图

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')
...
plt.show()

散点图

plt.scatter(x_np, y_relu)