这道题的写法大体有两种:大法师DFS和并查集,两种算法都不难,本篇博客主要讲解DFS,而且测试数据特水,连个剪枝都不用都可以过。
题目描述[luogu传送门]
现有一块大奶酪,它的高度为 h,它的长度和宽度我们可以认为是无限大的,奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系,在坐标系中, 奶酪的下表面为z = 0,奶酪的上表面为z = h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别 地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果 一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在 不破坏奶酪 的情况下,能否利用已有的空洞跑 到奶酪的上表面去?
空间内两点P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
Dist(P1,P2)=√[(x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
输入输出格式
输入格式:
每个输入文件包含多组数据。
的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T 组数据,每组数据的格式如下: 第一行包含三个正整数 n,h 和 r,两个数之间以一个空格分开,分别代表奶酪中空 洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数 x,y,z两个数之间以一个空格分开,表示空 洞球心坐标为(x,y,z)。
输出格式:
T 行,分别对应 T组数据的答案,如果在第 i 组数据中,Jerry 能从下 表面跑到上表面,则输出Yes,如果不能,则输出No (均不包含引号)。
这道题思路很简单,然而却比较容易打错,对于判定条件可能把握不准。
首先搜索一遍找到与下底相切或者相交的圆开始走下去。
如果走到最顶端就return了,并且让对错标记为对。
但是的但是的但是------代码实现上却并非想象的那么简单。
这里需要维护一个vis数组。
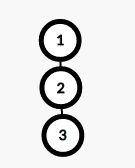
为什么?可以想象成一个如下一个无向图
如果不去维护,让1走到2,2又走回1,这就和于跑图时的环很像,以至于DFS会无限递归,从而爆掉。
在每次DFS的时候,递归一个点的标号,都需要让vis[i]=true
在每次走的时候是绝对不能走已经vis了的。
以下是AC代码:(不开 long long 见祖宗!!!)
#include#define INT long long #define is_cnct(i,j) (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])+(z[i]-z[j])*(z[i]-z[j])<=4*r*r inline void read(long long &x){ int f=1;x=0;char s=getchar(); while(s>'9' || s<'0') {if(s=='-')f=-1;s=getchar();} while(s<='9' && s>='0') {x=x*10+s-'0';s=getchar();} x*=f; } inline void print(long long x){ if(x<0) putchar('-'),x=-x; if(x>9) print(x/10); putchar(x%10+'0'); } using namespace std; const int maxn=10000; //------------------------- INT x[maxn],y[maxn],z[maxn]; bool vis[maxn],mark; INT n,h,r; char yes[]="Yes\n"; char no[]="No\n"; //------------------------- void init(){ mark=false; n=0,h=0,r=0; memset(vis,false,sizeof(vis)); } //------------------------ void dfs(int u) { if(z[u]+r>=h){mark=true;return;} if(mark) return; vis[u]=true; for(int i=1;i<=n;++i) if(!vis[i] && is_cnct(u,i)) dfs(i); } int main(int arrc,char* arrv[]) { //freopen("input.txt","r",stdin); INT T; read(T); while(T--) { init(); read(n),read(h),read(r); for(int i=1;i<=n;++i) read(x[i]),read(y[i]),read(z[i]); for(int i=1;i<=n;++i) if(!vis[i] && z[i]<=r) dfs(i); mark?printf(yes):printf(no); } return 0; }
并查集我没有写,原理是让所有可连接的点连接,sort后两重循环判定后查找1号点和n号点是否在同一集合里面。
虽然我也不知道为什么昨晚上一个小时都没有弄出来,还是今早上15分钟就写好了。。。。