从递归看栈
很早之前就看过《码农翻身》中的一篇文章----“递归那点事儿”。
一直很迷恋计算机底层操作系统的故事,却也深感计算机世界的庞大。在前前后后看了这篇文章不下十遍之后,也在不断地积累之后,现在写这篇文章,作为对栈的进一步理解的总结。
一:伊始,暗潮涌动:
问题:
计算5的阶乘;(我使用javascript)
function test(n){
if(n == 1){
return 1;
}else if(n <= 0){
return 0;
}else{
return n * test(n-1);
}
}
console.log(test(5));
运行结果:
![]()
分析:上述代码就是递归,通俗的讲就是自己调用自己;
在执行函数test时,他也调用了另外一个函数,只不过这个函数的代码和上一个函数的代码一模一样!是不是很简单 -_-
看一下机器层面的执行过程:
此时就需要引入栈帧的概念了:
1:栈帧将栈分割成N个记录块,每一个记录块的大小是不一样的;
2:这个记录块实际上是编译器用来实现函数调用的数据结构,通俗来讲就是用于活动记录,他用于记录每次函数调用所涉及的相关信息的记录单元;
3:栈帧也是一个函数的执行环境,它包括函数的参数,函数的局部变量函数,执行完之后要返回到哪里等等;
说到这里貌似,大约,好像明白了栈帧原来是用于调用函数的,你每调用一次函数他就会形成一个栈帧用于这个被调用函数的运行环境;
说到这,貌似懂了:上边的test函数在运行时就是形成了一个又一个栈帧啊!
针对上边的递归函数,我画了一幅函数在栈中的执行示意图;
栈是一种先进后出的数据结构!!!
分析:
要求计算5的阶乘;
1):调用test函数时传入5,即首先在栈中划出一个记录块做为函数test(5)的执行环境;执行到最后结果为: 5 * test(4);
2):上一个函数的返回值中调用函数test(4),因此继续指向新的记录块,用于执行函数test(4);执行到最后结果为: 4 * test(3);
3):上一个函数的返回值中调用函数test(3),因此继续指向新的记录块,用于执行函数test(3);执行到最后结果为: 3 * test(2);
4):上一个函数的返回值中调用函数test(2),因此继续指向新的记录块,用于执行函数test(2);执行到最后结果为: 2 * test(1);
5):上一个函数的返回值中调用函数test(1),因此继续指向新的记录块,用于执行函数test(1);执行到最后test(1)=1;
此时进栈操作已经到达了递归终止的条件,为了计算出最后的test(5)的值需要执行出栈操作;
如上图,我画了一幅出栈示意图;栈是先进后出的,所以最后进的要先出。
1):test(1)出栈,返回值为1;
2):栈帧test(2)接收test(1)返回值进行计算得出test(2) = 2 * 1 = 2;
3):test(2)出栈,栈帧test(3)接收test(2)返回值进行计算得出test(3) = 3 * 2 = 6;
4):test(3)出栈,栈帧test(4)接收test(3)返回值进行计算得出test(4) = 4 * 6 = 24;
5):test(4)出栈,栈帧test(5)接收test(4)返回值进行计算得出test(5) = 5 * 24 = 120;
6):test(5)出栈,返回值120,此时表示这一段程序已经执行完毕,计算得出5的阶乘是120;
递归函数写到这一步,貌似是已经完美了,但是你有没有想过:每一个函数test(n) = n * test (n-1)因此每一个栈帧不仅需要保存n值还要记录下一个栈帧的返回值,然后才能计算出来当前栈帧的结果,因此使用多个栈帧是不可避免的,计算5的阶乘就使用了5个栈帧,那要是计算100的呢?10000的呢?。。。。这TM是不是有点始料未及了?栈的大小也是有限的,你就这么用下去,他不给你溢出才怪。因此我给这一节命名为:“伊始,暗潮涌动”;
二:锤炼,万法归一
上边的程序就已经暴露出来了缺陷,也就是栈的大小是有限的,所以上述递归函数是可以优化的;
优化后的函数为:
function newTest(n,result){
if(n == 1){
return 1;
}else if(n <= 0){
return 0;
}else{
return newTest(n - 1,n * result);
}
}
console.log(test(5));执行结果为:
![]()
分析:鉴于前边递归函数的缺陷,修改了递归算法如上述代码,不知道你有没有发现每一次递归时return的内容不再是一个表达式,而是这个函数本身!这个好处是巨大的!因为他使用一个栈帧就可以搞定!这个函数有着良好的栈帧复用性!这种方式也就是传说中的尾递归了!
为什么前边的栈帧就不可以复用呢?咱们假设他也是可以复用的,他要是复用了岂不是把先前保存的n值丢掉了?那后边的test(n-1)计算出来之后还有什么用?因此他是绝对做不到复用的!
在尾递归中返回值不是表达式的一部分,也就是说他栈帧的复用不会有任何的隐患,不会管头不顾腚-_- 所以当返回值不是表达式的一部分时也就可以称为尾递归了;
最后的话:
1 : 这是优化吗?在明白了道理之后,怕就不能再称之为优化了吧,而是必须应当要做的!
A:你会优化递归吗?
B:什么优化?栈帧复用难道不是要直接考虑进来的吗?
2:最后,离不开的只是习惯而已;
递归的基本思想
所谓递归,就是有去有回。
递归的基本思想,是把规模较大的一个问题,分解成规模较小的多个子问题去解决,而每一个子问题又可以继续拆分成多个更小的子问题。
最重要的一点就是假设子问题已经解决了,现在要基于已经解决的子问题来解决当前问题;或者说,必须先解决子问题,再基于子问题来解决当前问题。
或者可以这么理解:递归解决的是有依赖顺序关系的多个问题。
我们假设一个抽象问题有两个时间点要素:开始处理,结束处理。
那么递归处理的顺序就是,先开始处理的问题,最后才能结束处理。
假设如下问题的依赖关系:
【A】----依赖---->【B】----依赖---->【C】
我们的终极目的是要解决问题A,
那么三个问题的处理顺序如下:
开始处理问题A;
由于A依赖B,因此开始处理问题B;
由于B依赖C,开始处理问题C;
结束处理问题C;
结束处理问题B;
结束处理问题A。从函数调用看广义递归
对于软件来说,函数的调用关系就是一个广义递归的过程,如下,
func_A()
{
func_B();
}
func_B()
{
func_C();
}
func_C()
{
/////
}
调用函数A;
调用函数B;
调用函数C;
函数C返回;
函数B返回;
函数A返回;狭义递归函数
有一种特例,就是处理问题A/B/C的方法是一样的,这就是产生了狭义的“递归函数“,即函数内又调用函数自身。
从上述分析看,递归对问题的处理顺序,是遵循了先入后出(也就是先开始的问题最后结束)的规律。
先入后出?栈!
没错,广义递归问题的处理,需要用栈来解决。经典的例子就是函数调用,就是依靠栈来实现的。
递归函数的非递归化
现在再来深入分析一下狭义的递归函数(也就是函数调用自身)。
我们知道递归函数存在的最大问题是,当递归次数足够大时,会导致函数栈溢出而死机,函数栈的大小一般是一个固定值,对于linux来说一般默认是8M。
因此,编程老司机会教导我们,不得用递归函数!但递归函数的代码实现实在是简洁啊,不让用?臣妾做不到啊!
那么问题来了,所有递归函数都能非递归化吗?答案是肯定的。
本质上讲,对于同一个问题,如果必然要用广义递归的方案来处理,那么狭义递归函数只不过是其中的一种实现方式,如果放弃狭义递归函数的话,我们不得不借助一个额外的数据结构:栈。
如此看来,无论如何都要用到栈,只不过要么让编译器来维护一个栈(函数栈),要么让程序狗来维护一个栈(数据栈)。
这两个栈的区别如下:
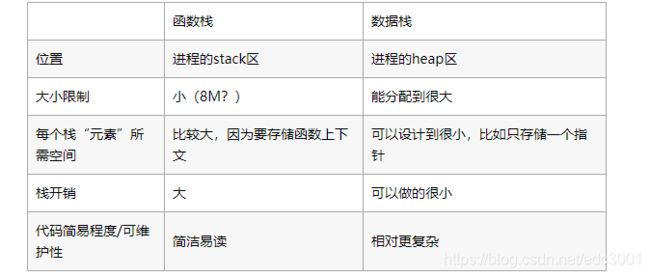
注:函数栈开销是一个绝对值,但也算是一个“相对“概念,一个非量化的理性分析是,内部逻辑越简单的函数,栈开销的影响越大,因为函数的出入栈指令占整个函数体指令的比重较大。
很多情况下,代码的易维护性是一个比性能开销更加重要的因素,因此,只要实际应用中不会造成函数栈溢出,我个人是更建议采用递归函数法的。
举例说明:二叉树的非递归遍历
非递归算法的递归化
既然递归算法可以用数据栈来进行非递归化,那么借助数据栈而实现的非递归算法,理论上也可以被递归化。也就是说,两者是可逆的,桥梁就是栈。