优化器
原文链接:https://www.yuque.com/yahei/hey-yahei/optimizer
参考:
- 《Hands-On Machine Learning with Scikit-Learn and TensorFlow(2017)》Chap11
- torch.optim
常见的加速训练技术:
- 恰当的的权重初始化策略:打破初始值的对称性,初始值也不能太小
- 恰当的激活函数:选用导数数值范围稍大的函数
- 批量归一化:平滑损失平面
- 复用部分预训练网络:复用预训练结果
- 使用恰当的优化器:开源项目中最常见的是SGD, NAG, RMSProp, Adam
常见优化器
传统梯度下降(Stochastic Gradient Descent, SGD)
参考:《机器学习-吴恩达 - 绪论、线性回归与逻辑回归 - 梯度下降算法 | Hey~YaHei!》
θ n = θ n − 1 − η ∂ J ( θ n ) ∂ θ n \theta_n = \theta_{n-1} - \eta \frac{\partial J(\theta_n)}{\partial \theta_n} θn=θn−1−η∂θn∂J(θn)
固定的下降速度
动量法(Momentum)
论文:《Some methods of speeding up the convergence of iteration methods(1964)》
m n = β m n − 1 + η ∂ J ( θ n ) ∂ θ n , 0 < = β < = 1 θ n = θ n − 1 − m n \begin{aligned} m_n &= \beta m_{n-1} + \eta \frac{\partial J(\theta_n)}{\partial \theta_n}, 0 <= \beta <= 1 \\ \theta_n &= \theta_{n-1} - m_{n} \end{aligned} mnθn=βmn−1+η∂θn∂J(θn),0<=β<=1=θn−1−mn
引入新的超参数 β \beta β 与先前的 m m m 相乘,以继承先前的动量,并防止动量过快增长;
SGD可以看作是 m n = η ∂ J ( θ n ) ∂ θ n m_n =\eta \frac{\partial J(\theta_n)}{\partial \theta_n} mn=η∂θn∂J(θn)的情形;
动量法相当于对参数的更新量做了平滑累积,每次迭代的更新量都包含了前几次更新量的效应。
记第 i i i次迭代中 Δ i = η ∂ J ( θ n ) ∂ θ n \Delta_i = \eta \frac{\partial J(\theta_n)}{\partial \theta_n} Δi=η∂θn∂J(θn),则有 m i = β m i − 1 + Δ i m_i = \beta m_{i-1} + \Delta_i mi=βmi−1+Δi,展开有
m n = β n − 1 Δ 1 + β n − 2 Δ 2 + . . . + β Δ n − 1 + Δ n m_n = \beta^{n-1}\Delta_1 + \beta^{n-2}\Delta_2 + ... + \beta\Delta_{n-1} + \Delta_n mn=βn−1Δ1+βn−2Δ2+...+βΔn−1+Δn
考虑 Δ 1 = Δ 2 = . . . = Δ n = Δ \Delta_1 = \Delta_2 = ... = \Delta_n = \Delta Δ1=Δ2=...=Δn=Δ,则 m n = 1 − β n 1 − β Δ m_n = \frac{1 - \beta^n}{1 - \beta} \Delta mn=1−β1−βnΔ;
当 n → ∞ n \rightarrow \infty n→∞时, m n = 1 1 − β Δ m_n = \frac{1}{1-\beta} \Delta mn=1−β1Δ,下降速度为SGD的 1 1 − β \frac{1}{1-\beta} 1−β1倍。
当 β = 0 \beta=0 β=0时为完全摩擦(退化为传统梯度下降);
当 β = 1 \beta=1 β=1时为完全光滑;
通常来说取 β = 0.9 \beta=0.9 β=0.9,此时下降速度理论上变为传统梯度下降的10倍。
涅斯捷罗夫加速梯度(Nesterov Accelerated Gradient, NAG)
论文:《A method of solving a convex programming problem with convergence rate O(1/k^2)(1983)》
m n = β m n − 1 + η ∂ J ( θ n + β m ) ∂ θ n , 0 < = β < = 1 θ n = θ n − 1 − m n \begin{aligned} m_n &= \beta m_{n-1} + \eta \frac{\partial J(\theta_n + \beta m)}{\partial \theta_n} , 0 <= \beta <= 1 \\ \theta_n &= \theta_{n-1} - m_n \end{aligned} mnθn=βmn−1+η∂θn∂J(θn+βm),0<=β<=1=θn−1−mn
动量法的变体,比动量法更快,而且振荡更小;
与动量法相比,区别在于计算的是损失函数在 θ + β m \theta + \beta m θ+βm 上而不是 θ \theta θ 上的梯度:

AdaGrad
论文:《Adaptive Subgradient Methods for Online Learning and Stochastic Optimization(2011)》
s n = s n − 1 + ( ∂ J ( θ n ) ∂ θ n ) 2 θ n = θ n − 1 − η s n + ϵ ⋅ ∂ J ( θ n ) ∂ θ n \begin{aligned} s_n &= s_{n-1} + (\frac{\partial J(\theta_n)}{\partial \theta_n})^2 \\ \theta_n &= \theta_{n-1} - \frac{\eta}{\sqrt{s_n + \epsilon}} \cdot \frac{\partial J(\theta_n)}{\partial \theta_n} \end{aligned} snθn=sn−1+(∂θn∂J(θn))2=θn−1−sn+ϵη⋅∂θn∂J(θn)
ϵ \epsilon ϵ通常取 1 0 − 10 10^{-10} 10−10来防止 s = 0 s=0 s=0的情况;
本质是为学习率增加一个感知损失累积效应的因子来动态调整学习率,训练前期 s s s较小,等效学习率较大,训练速度比较快;随着训练过程的推进, s s s逐渐增大,等效学习率降低,减小振荡的出现,便于找到局部最优点。
考虑两权重梯度差异显著的情况(如图, θ 1 \theta_1 θ1平缓, θ 2 \theta_2 θ2陡峭),
传统的梯度下降,会在陡峭的 θ 2 \theta_2 θ2上很快到达一个比较的位置,而平缓的 θ 1 \theta_1 θ1方向上梯度下降缓慢;
而AdaGrad能够响应这种特殊情况,从而加速梯度下降。

RMSProp
该优化器由eoffrey Hinton在其课堂上提出,而没有形成正式的论文,研究者通常用 slide 29 in lecture 6 来引用它, 幻灯片 、 视频 ;
s n = β s n − 1 + ( 1 − β ) ( ∂ J ( θ n ) ∂ θ n ) 2 θ n = θ n − 1 − η s n + ϵ ⋅ ∂ J ( θ n ) ∂ θ n \begin{aligned} s_n &= \beta s_{n-1} + (1 - \beta) (\frac{\partial J(\theta_n)}{\partial \theta_n})^2 \\ \theta_n &= \theta_{n-1} - \frac{\eta}{\sqrt{s_n + \epsilon}} \cdot \frac{\partial J(\theta_n)}{\partial \theta_n} \end{aligned} snθn=βsn−1+(1−β)(∂θn∂J(θn))2=θn−1−sn+ϵη⋅∂θn∂J(θn)
RMSProp是AdaGrad的变体,在AdaGrad的基础上增加了一个指数平滑平均的效果(通常取 β = 0.9 \beta = 0.9 β=0.9),解决了AdaGrad学习率衰减偏快的问题。
Adam
论文:《ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION(2015)》
动量法和RMSProp的集成。
m n = β 1 m n − 1 + ( 1 − β 1 ) ∂ J ( θ n ) ∂ θ n s n = β 2 s n − 1 + ( 1 − β 2 ) ( ∂ J ( θ n ) ∂ θ n ) 2 m ^ n = m n 1 − β 1 n s ^ n = s n 1 − β 2 n θ n = θ n − 1 − η s ^ n − ϵ m \begin{aligned} m_n &= \beta_1 m_{n-1} + (1-\beta_1) \frac{\partial J(\theta_n)}{\partial \theta_n} \\ s_n &= \beta_2 s_{n-1} + (1-\beta_2) (\frac{\partial J(\theta_n)}{\partial \theta_n})^2 \\ \hat{m}_n &= \frac{m_n}{1 - \beta_1^n} \\ \hat{s}_n &= \frac{s_n}{1 - \beta_2^n} \\ \theta_n &= \theta_{n-1} - \frac{\eta}{\sqrt{\hat{s}_n - \epsilon}} m \end{aligned} mnsnm^ns^nθn=β1mn−1+(1−β1)∂θn∂J(θn)=β2sn−1+(1−β2)(∂θn∂J(θn))2=1−β1nmn=1−β2nsn=θn−1−s^n−ϵηm
m n m_n mn和 s n s_n sn分别是对梯度的一次估计和二次估计, m ^ n \hat{m}_n m^n和 s ^ n \hat{s}_n s^n是对 m n m_n mn和 s n s_n sn的无偏估计;
通常,取 β 1 = 0.9 , β 2 = 0.999 , ϵ = 1 0 − 8 , η = 0.001 \beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}, \eta = 0.001 β1=0.9,β2=0.999,ϵ=10−8,η=0.001
Jacobian优化 & Hessian优化
以上讨论都是基于一次偏导的Jacobian矩阵,实际上用基于二次偏导的Hessian矩阵可以取得更好的优化效果。
但这很难应用到DNN上,因为每层都会输出 n 2 n^2 n2个Hessian矩阵(如果是Jacobian,只需要n个),其中n是参数数量,而DNN参数数量大的惊人,所以基于Hessian的优化反而会因为计算大量的Hessian矩阵而速度下降并且需要大量的空间来进行计算。
学习计划(Learning Schedules)
如图,当学习率太低时训练过慢,学习率太高时不容易得到最优解;
可以在开始训练时给一系列不同的学习率跑一小段时间,比较它们的loss曲线,来确定一个比较合适的学习率;
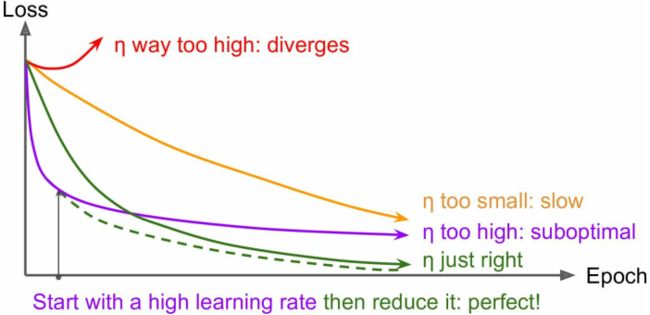
除此之外,还有一些有用的策略,称为学习计划learning schedules——
- 分段常数学习率(Predetermined piecewise constant learning rate)
预设好每过多少epochs就改变学习率,需要比较多的人工调整
- 性能调整(Performance scheduling)
每N步用验证集计算一次loss,当loss不再减小的时候衰减学习率(通常乘以一个因子 γ \gamma γ)
-
随时间指数衰减(Exponential scheduling)
η ( t ) = η 0 1 0 − t / r \eta(t) = \eta_0 10^{-t/r} η(t)=η010−t/r
t t t为迭代次数, η 0 \eta_0 η0和 r r r是人工设置的超参数,学习率每 r r r步衰减一次 -
随时间乘方衰减(Power scheduling)
η ( t ) = η 0 ( 1 + t / r ) − c \eta(t) = \eta_0 (1+t/r)^{-c} η(t)=η0(1+t/r)−c
通常取 c = 1 c=1 c=1,有点类似Exponential scheduling,但衰减速度稍微慢一些
论文《AN EMPIRICAL STUDY OF LEARNING RATES IN DEEP NEURAL NETWORKS FOR SPEECH RECOGNITION(2013) 》比较了一些主流的学习计划——
在语音识别任务中使用动量法优化的前提下,
- Performance Scheduling和Exponential Scheduling都表现的很好
- 但是Exponential Scheduling容易实现、容易调整、收敛更快