反卷积(Deconvolution)、上采样(UNSampling)与上池化(UnPooling)加入自己的思考（pytorch函数）（二）

ps之前写过反卷积(Deconvolution)、上采样(UNSampling)与上池化(UnPooling)加入自己的思考（一），不过那是东拼西凑出来的别人的东西就是稍微加入点自己的理解。今天在看代码时候又出现上池化和反卷积这两个选项。最终作者的代码里是用了反卷积但是我还是想更细理解什么时候用反卷积什么时候用上池化啊。刚刚写完保存不了，被我误关了。想哭啊啊！后面部分要再来一遍额。写简单一些了。

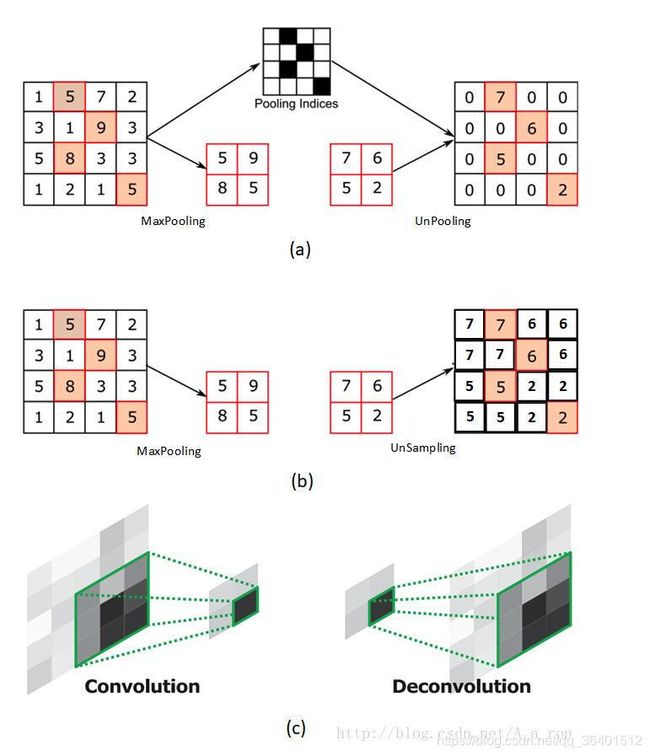
之前博文里可以看到三者是这样的：https://blog.csdn.net/A_a_ron/article/details/79181108参考的博文

但是上面只是别人画了图，实际真没形成代码呢。（目前在用pytorch框架，故将之前的tensorflow换成pytorch）

上池化，贴一下我的代码和结果：

import torch
from torch import nn
from torch.autograd import Variable
a = torch.Tensor([[[[2, 3, 4, 4],
                   [3, 4, 8, 4],
                   [7, 3, 5, 8],
                   [2, 3, 4, 4]]]]
                 )
print(a)
a= Variable(a.cuda(async = True))
pool= nn.MaxPool2d(2,stride=2,return_indices =True)
p,i=pool(a)
print('p',p)
unpool = nn.MaxUnpool2d(2,stride=2)
up=unpool(p,i)
print('up',up)

(0 ,0 ,.,.) = 
  2  3  4  4
  3  4  8  4
  7  3  5  8
  2  3  4  4
[torch.FloatTensor of size 1x1x4x4]

('p', Variable containing:
(0 ,0 ,.,.) = 
  4  8
  7  8
[torch.cuda.FloatTensor of size 1x1x2x2 (GPU 0)]
)
('up', Variable containing:
(0 ,0 ,.,.) = 
  0  0  0  0
  0  4  8  0
  7  0  0  8
  0  0  0  0
[torch.cuda.FloatTensor of size 1x1x4x4 (GPU 0)]
)

 

print('i',i)
('i', Variable containing:
(0 ,0 ,.,.) = 
   5   6
   8  11
[torch.cuda.LongTensor of size 1x1x2x2 (GPU 0)]
)

还真和图中一样，其中原来pool时候产生的是两个参数，一个记录结果一个结果p，一个记录位置i。然后在上池化时候输入结果p和位置i便能还原到原来的位置。

 

unspamle= nn.UpsamplingNearest2d(scale_factor=2)
us=unspamle(p)
print('us',us)

)
('us', Variable containing:
(0 ,0 ,.,.) = 
  4  4  8  8
  4  4  8  8
  7  7  8  8
  7  7  8  8
[torch.cuda.FloatTensor of size 1x1x4x4 (GPU 0)]
)

也是跟上图里的一样，那么也就理解了上采样和上池化的差异（实际代码中），而反卷积其实就是转置卷积，具体可以看我之前的博客。（这里开始没保存可恶！！！）。

这里理解上池化和转置卷积差异：上论文《Learning Deconvolution Network for Semantic Segmentation》的理解图

图（a）是输入层；图（b）是14*14反卷积的结果；图（c）是28*28的UnPooling结果；图（d）是28*28的反卷积结果；图（e）是56*56的Unpooling结果；图（f）是56*56反卷积的结果；图（g）是112*112 UnPooling的结果；图（h）是112*112的反卷积的结果；图（i）和图（j）分别是224*224的UnPooling和反卷积的结果。
 

上图就是转置卷积和上池化的差异，我们可以发现：

1.当特征图中的目标像素点较少的时候，转置卷积更适合我们，上池化得到的结果分辨率太差了对比转置卷积得到的结果。

2.而当当特征图中的目标像素点较多的时候，上池化化更时候我们，上池化得到的结果轮廓细节清晰，分辨率也能接受。

而肺结节所用的模型中，一个较大的结节如20*20*20，在我们要用的特征图中已经变成了5*5*5，更不用说8*8*8已经变成2*2*2了。所以grt团队的代码选用了转置卷积啊。我也解开了其中的困惑。

 

PS2019年4月22日添加：

https://blog.csdn.net/tsyccnh/article/details/87357447 很好的图解了直接卷积和转置卷积的区别和实际运算中的卷积是怎么操作的。其中一句话特别形象解释了直接卷积和转置卷积（反卷积）的差异：

直接卷积我们是用一个“小窗户”去看一个“大世界”，而转置卷积是用一个“大窗户”的一部分去看“小世界”。这里有一点需要注意，我们定义的卷积核是左上角为a，右下角为i，但在可视化转置卷积中，需要将卷积核旋转180°后再进行卷积。