Imperial roads Gym - 101889I （LCA的另一种实现）

题意：   Q次询问，每次询问必须包含特定边的最小生成树。

思路： 考虑 最淳朴的最小生成树，如果加了一条特定边，肯定是构成了一个环，那么环外的边肯定是不变的，要不然，根本就不可能选外面的那些边了， 所以我们现在就是求这个环上的最小 生成树，肯定是找树上之前的 两个点之间的最大边，删掉就行了。

所以问题就变成了，求树上 任意两点之间的最大边。

 

错误思路： 考虑欧拉序列中深度的属性，想着可不可以求一个最大值。直接把边权给儿子，询问的时候直接查找 最大值就好了。

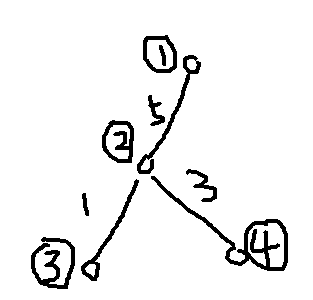
错误样例1： 找 3 4 之间的最大值，会把 5放进去，就很难受

 

错误样例2：找 1 和 5 的最大值， dfs的时候，可能会很恐怖的先走 1234325，  所以本来不属于路径上的点也会被加进来

 

正确思路： 记录 fa[i][j]  //表示 的上面距离为 的祖先是谁

           同样记录 dis[i][j] //表示 的上面距离为 范围内的最大边权

 

然后就是LCA的跳跃了

 

#include
using namespace std;
typedef long long LL;

#define rep(i,a,b) for(int i=a;i=a;--i)

map,int> id;
const int N=1e5+10;

int has[N*2];

struct Edge{
	int u,v,w,nt;
	Edge(int _u=0,int _v=0,int _w=0,int _nt=0){
		u=_u,v=_v,w=_w,nt=_nt;
	}
}edge[N*4],e[N*4];
int head[N],cnt;
void add_edge(int u,int v,int w){
	edge[cnt]=Edge(u,v,w,head[u]);
	head[u]=cnt++;
}

int cmp(Edge a,Edge b){
	return a.wdep[y])swap(x,y);
	int ans=swim(y,dep[y]-dep[x]);
	if(x==y)return ans;//如果x 就是Y的祖先，那么久结束了
	for(int i=mx_h;i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			ans=max(ans,dis[x][i]);
			ans=max(ans,dis[y][i]);
			x=fa[x][i];
			y=fa[y][i];
		}
	}
	//printf("x:%d y:%d\n",x,y);
	ans=max(ans,dis[x][0]);
	ans=max(ans,dis[y][0]);
	return ans;
}


int main(){
	Log[1]=0;
	rep(i,2,N)Log[i]=Log[i/2]+1;

	int n,m;
	scanf("%d %d",&n,&m);

	cnt=0;
	rep(i,0,n+1){
		head[i]=-1;
		pre[i]=i;
	}

	rep(i,0,m){
		int u,v,w;
		scanf("%d %d %d",&u,&v,&w);
		e[i]=Edge(u,v,w);
	}

	sort(e,e+m,cmp);
	rep(i,0,m)id[make_pair(e[i].u,e[i].v)]=i;

	int sum=0;
	rep(i,0,m){
		Edge& ee=e[i];
		if(join(ee.v,ee.u)){
			sum+=ee.w;
			has[i]=1;
			add_edge(ee.u,ee.v,ee.w);
			add_edge(ee.v,ee.u,ee.w);
		}
	}

	dfs(1,0,0);
	QQQ(n);

	int q;
	scanf("%d",&q);
	rep(i,0,q){
		int u,v;
		scanf("%d %d",&u,&v);
		int dd=id[make_pair(u,v)];
		if(has[dd]){
			printf("%d\n",sum);
			continue;
		}
		int w=LCA(u,v);
		printf("%d\n",sum-w+e[dd].w);
	}

	return 0;
}