cs231n课程:图像分类笔记
图像是一个由数字组成的巨大的三维数组。
在这个例子中,猫的图像大小是宽248像素,高400像素,有3个颜色通道,分别是红、绿和蓝(简称RGB)。如此,该图像就包含了248X400X3=297600个数字,每个数字都是在范围0-255之间的整型,其中0表示全黑,255表示全白。我们的任务就是把这些上百万的数字变成一个简单的标签,比如“猫”。
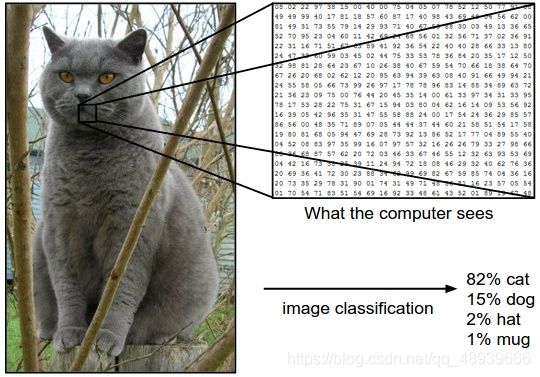
采用数据驱动算法
给计算机很多数据,然后实现学习算法,让计算机学习到每个类的外形。这种方法,就是数据驱动方法。
图像分类的步骤
在课程视频中已经学习过,图像分类就是输入一个元素为像素值的数组,然后给它分配一个分类标签。完整流程如下:
输入:输入是包含N个图像的集合,每个图像的标签是K种分类标签中的一种。这个集合称为训练集。
学习:这一步的任务是使用训练集来学习每个类到底长什么样。一般该步骤叫做训练分类器或者学习一个模型。
评价:让分类器来预测它未曾见过的图像的分类标签,并以此来评价分类器的质量。我们会把分类器预测的标签和图像真正的分类标签对比。毫无疑问,分类器预测的分类标签和图像真正的分类标签如果一致,那就是好事,这样的情况越多越好。
Nearest Neighbor分类器
Nearest Neighbor算法将会拿着测试图片和训练集中每一张图片去比较,然后将它认为最相似的那个训练集图片的标签赋给这张测试图片。
最简单的方法就是逐个像素比较,最后将差异值全部加起来。换句话说,就是将两张图片先转化为两个向量,然后计算他们的L1距离:
[公式]


如果两张图片一模一样,那么L1距离为0,但是如果两张图片很是不同,那L1值将会非常大。
代码分析
让我们看看如何用代码来实现这个分类器。首先,我们将CIFAR-10的数据加载到内存中,并分成4个数组:训练数据和标签,测试数据和标签。在下面的代码中,Xtr(大小是50000x32x32x3)存有训练集中所有的图像,Ytr是对应的长度为50000的1维数组,存有图像对应的分类标签(从0到9):
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # 我们提供的一个神奇的功能
# 将所有图像平展成一维
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows变成50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows变成10000 x 3072
接下来展示如何训练并评价一个分类器:
nn = NearestNeighbor() # 创建最近邻分类器类
nn.train(Xtr_rows, Ytr) # 在训练图像和标签上训练分类器
Yte_predict = nn.predict(Xte_rows) # 预测测试图像上的标签
# 现在打印分类精度,也就是平均值
# 正确预测的示例(例如,标签匹配)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )
下面就是使用L1距离的Nearest Neighbor分类器的实现套路:
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.ytr = y
def predict(self, X):
""" X is N x D 每一行都是我们希望预测标签的一个例子 """
num_test = X.shape[0]
# 让我们确保输出类型与输入类型匹配
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# 循环所有测试行
for i in xrange(num_test):
# 找出与第i个测试图像最近的训练图像
# 使用L1距离(绝对值差之和)
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances) # 得到距离最小的索引
Ypred[i] = self.ytr[min_index] # 预测最近示例的标签
return Ypred
距离算法的选择
L2距离算法

在Numpy中,我们只需要替换上面代码中的1行代码就行:
distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
L1和L2比较。比较这两个度量方式是挺有意思的。在面对两个向量之间的差异时,L2比L1更加不能容忍这些差异。也就是说,相对于1个巨大的差异,L2距离更倾向于接受多个中等程度的差异。L1和L2都是在p-norm常用的特殊形式。
k-Nearest Neighbor分类器
Nearest Neighbor分类器是找到最相似的一个图片的标签,而k-Nearest Neighbor是找到相似的k张图片,然后针对测试图片进行投票。所以当k=1的时候,k-Nearest Neighbor分类器就是Nearest Neighbor分类器。从直观感受上就可以看到,更高的k值可以让分类的效果更平滑,使得分类器对于异常值更有抵抗力。
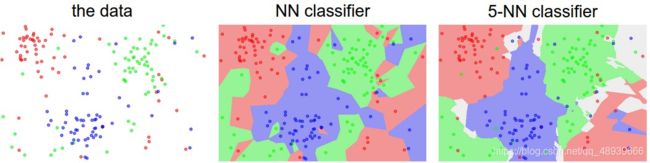
测试数据集只使用一次,即在训练完成后评价最终的模型时使用。
Nearest Neighbor分类器在某些特定情况(比如数据维度较低)下,可能是不错的选择。但是在实际的图像分类工作中,很少使用。因为图像都是高维度数据(他们通常包含很多像素),而高维度向量之间的距离通常是反直觉的。下面的图片展示了基于像素的相似和基于感官的相似是有很大不同的:
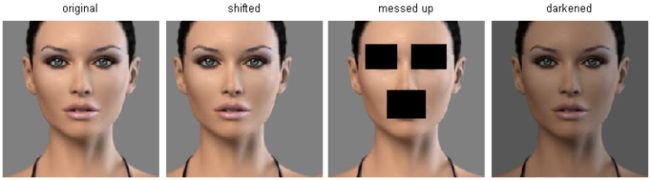
在高维度数据上,基于像素的的距离和感官上的非常不同。上图中,右边3张图片和左边第1张原始图片的L2距离是一样的。很显然,基于像素比较的相似和感官上以及语义上的相似是不同的。
小结:实际应用K-NN
如果你希望将k-NN分类器用到实处(最好别用到图像上,若是仅仅作为练手还可以接受),那么可以按照以下流程:
1,预处理你的数据:对你数据中的特征进行归一化(normalize),让其具有零平均值(zero mean)和单位方差(unit variance)。在后面的小节我们会讨论这些细节。本小节不讨论,是因为图像中的像素都是同质的,不会表现出较大的差异分布,也就不需要标准化处理了。
2,如果数据是高维数据,考虑使用降维方法,比如PCA(wiki ref, CS229ref, blog ref)或随机投影。
3,将数据随机分入训练集和验证集。按照一般规律,70%-90% 数据作为训练集。这个比例根据算法中有多少超参数,以及这些超参数对于算法的预期影响来决定。如果需要预测的超参数很多,那么就应该使用更大的验证集来有效地估计它们。如果担心验证集数量不够,那么就尝试交叉验证方法。如果计算资源足够,使用交叉验证总是更加安全的(份数越多,效果越好,也更耗费计算资源)。
4,在验证集上调优,尝试足够多的k值,尝试L1和L2两种范数计算方式。
5,如果分类器跑得太慢,尝试使用Approximate Nearest Neighbor库(比如FLANN)来加速这个过程,其代价是降低一些准确率。
6,对最优的超参数做记录。记录最优参数后,是否应该让使用最优参数的算法在完整的训练集上运行并再次训练呢?因为如果把验证集重新放回到训练集中(自然训练集的数据量就又变大了),有可能最优参数又会有所变化。在实践中,不要这样做。千万不要在最终的分类器中使用验证集数据,这样做会破坏对于最优参数的估计。直接使用测试集来测试用最优参数设置好的最优模型,得到测试集数据的分类准确率,并以此作为你的kNN分类器在该数据上的性能表现。