UFDL Tutorial - Unsupervised Learning

Unsupervised Learning

Preprocessing: PCA and Whitening

PCA

Whitening

白化的目的就是降低输入的冗余性，即想通过白化过程使得输入：

1. 特征间的相关性较低；(PCA)
2. 所有特征具有相同的方差。($\frac{1}{\sqrt{{\lambda }_i+ϵ}}$缩放)

PCA已经使得数据间的相关性降低，为使每个输入特征具有单位方差，用$\frac{1}{\sqrt{{\lambda }_i+ϵ}}$作为缩放因子（$ϵ$用于正则化，防止分母为零，导致数据上溢到无穷，同时具有平滑即低通滤波作用），缩放每个特征$x_{rot,i}$，即PCA白化后的数据$x_{PCAwhite}$满足：

$$x_{PCAwhite,i}=\frac{x_{rot,i}}{\sqrt{{\lambda }_i+ϵ}},i代表成分或维度$$

PCA白化后的数据已经具有单位协方差，ZCA白化是在PCA白化的基础上，左乘一个任意正交矩阵$R$（$R{R}^T=R^{T}R=I$，也可以是旋转或反射矩阵），那么处理后的数据仍然具有单位协方差，在ZCA白化中，取PCA投影矩阵$R=U$，则：

$$x_{ZCAwhite}=U{x}_{PCAwhite}$$

这种旋转使得$x_{ZCAwhite}$尽可能的接近原始数据$x$。

Implementing PCA/Whitening

1. 使数据均值为零；
2. 计算协方差矩阵；
3. 计算协方差矩阵的特征值和特征向量；
4. 使用特征向量组成的PCA变换矩阵$U$（旋转矩阵，按特征值大小降序且按列排）旋转数据，得到PCA变换后的数据$x_{rot}$，取前$k$个特征向量组成旋转矩阵旋转数据，得到PCA降维后的数据（假设输入$x\in R^n,k<n$）；
5. 使用$\frac{1}{\sqrt{{\lambda }_i+ϵ}}$对PCA旋转后的数据缩放，使其具有相同单位协方差，得到PCA白化后的数据$x_{PCAwhite}$；
6. 对PCA白化后的数据，左乘PCA变换矩阵得到ZCA白化后的数据$x_{ZCAwhite}$。

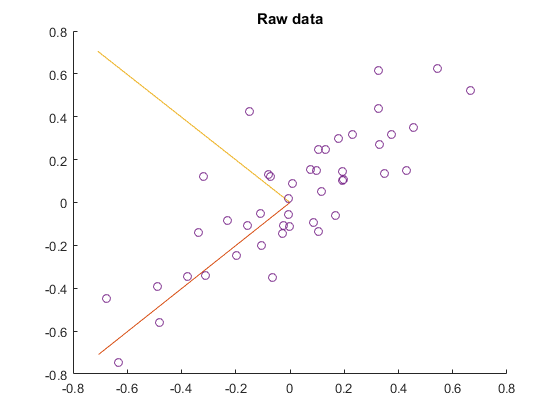
Exercise:PCA_in_2D

MATLAB实现：

• 使数据均值为零：（提供的二维数据以具有相同均值0，此步省去）

avg = mean(x, 1);
x = x - repmat(x, 1);

• 计算协方差矩阵：

sigma = cov(x', 1); % MATLAB function, '1' normalize with n
sigma = x*x'/size(x, 2); % or you can use this code

原始数据协方差：

sigma =
    0.0883    0.0733
    0.0733    0.0890

• 计算协方差矩阵的特征值和特征向量：

[U, S, ~] = svd(sigma);

结果图：

U =
   -0.7055   -0.7087
   -0.7087    0.7055
S =
    0.1620         0
         0    0.0154

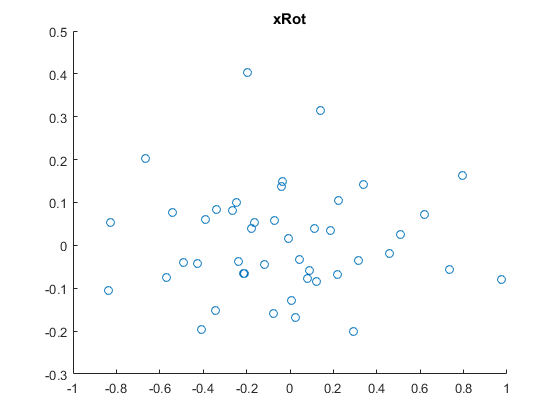
• PCA变换旋转数据$x$得到$x_{rot}$：

xRot = U'*x;

结果图：

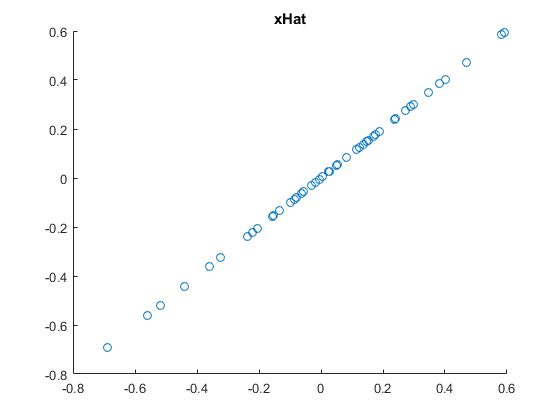
• PCA降维数据:

xRot = U(:,1:k)'*x; % projecting to 1 dimension
xHat = U(:,1:k)*xRot; % projecting the xRot back

结果图：

• PCA白化：

xPCAWhite = diag(1./sqrt(diag(S)+epsilon))*U'*x; % xPCAWhite_i = xRot_i/sqrt(lambda_i)

sigmaPCAWhite = cov(xPCAWhite', 1); % computes the covariance of PCAWhite data

结果图：

sigmaPCAWhite =
    0.9921    0.0066
    0.0066    0.9937

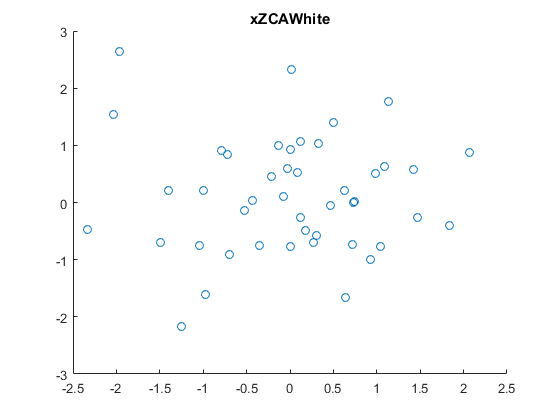
• ZCA白化：

xZCAWhite = U*diag(1./sqrt(diag(S)+epsilon))*U'*x; % xZCAWhite_i = U*xPCAWhite

sigmaZCAWhite = cov(xZCAWhite', 1); % computes the covariance of ZCAWhite data

结果图：

sigmaZCAWhite =
    0.9996   -0.0008
   -0.0008    0.9863

Exercise:PCA and Whitening

当把PCA应用于图像时，有点疑惑的是，按照协方差的公式：
$$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]$$，减去的均值应该是所有样本的均值。这样，对于图像块矩阵${\mathrm{x}}_{\mathrm{n}\times \mathrm{m}}$，其中，$n$为一个样本的特征维度即一个图像块拉成列向量的维度，$m$为图像块的数目，求其特征维上的协方差时，均值应该这样求：$\overline{\mathrm{x}}=\frac{1}{m}{\sum }_{i=1}^m{\mathrm{x}}^{(i)}$，而教程中是这样求的：$\overline{{\mathrm{x}}^{(i)}}=\frac{1}{n}{\sum }_{j=1}^n{\mathrm{x}}_j^{(i)}$，即每个块求均值。文中说我们对图像块的平均亮度值不感兴趣，所以可以减去这个值进行均值规整化。

So, we won’t use variance normalization. The only normalization we need to perform then is mean normalization, to ensure that the features have a mean around zero. Depending on the application, very often we are not interested in how bright the overall input image is. For example, in object recognition tasks, the overall brightness of the image doesn’t affect what objects there are in the image. More formally, we are not interested in the mean intensity value of an image patch; thus, we can subtract out this value, as a form of mean normalization.

Exercise: PCA Whitening

一点说明：教程中叙述的与展示的实验结果图不一致：文中叙述的是$144\times 10000$的矩阵（与Wiki上的教程一致），实验数据集却是手写体$784\times 60000$，这里也用手写体数据，可以到THE MNIST DATABASE下载。

• 零均值化数据

这里处理的是手写体图像，所以求得是每个图像块（patch）的均值。

% avg = mean(x, 1);
% x = x - repmat(avg, size(x,1), 1);
x = bsxfun(@minus, x, mean(x,1)); % or this code

结果如下：

• 旋转数据：

sigma = x*x'/m; % n-by-n
[u, s, ~] = svd(sigma);
xRot = u'*x;% n-by-m

• 验证PCA实现的正确性，即旋转数据的协方差仅对角元素非零：

covar = xRot*xRot'/m; % the mean of xRot is 0

结果图（原本784*784，缩放了一下，就得到教程中的结果）：

• 寻找保留主成分数目：

保留方差百分比：99%：

lambda = diag(s);
lambda_sum = sum(lambda);
lambda_sumk = 0;
perc = 0;
k = 0;
while perc < 0.99
    k = k + 1;
    lambda_sumk = lambda_sumk + lambda(k);
    perc = lambda_sumk / lambda_sum;
end

• 维数约简与重构：

xDimk = u(:,1:k)'*x;
xHat = u(:,1:k)*xDimk;

如果零均值化过程，采用所有图像块的均值，则零均值化后的图像和PCA重构后的图像如下图所示：

• PCA白化及检验：

通过观察白化后数据的协方差矩阵，分别使用不同的值正则化和不使用正则化（epsilon近似为0）：

epsilon = 1e-1; 
%%% YOUR CODE HERE %%%
xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x;

结果图：

• ZCA白化：

xZCAWhite = u*diag(1./sqrt(diag(s)+epsilon))*u'*x;