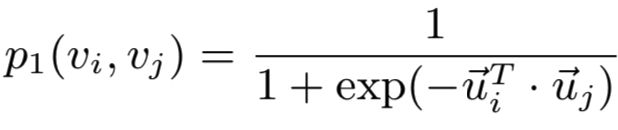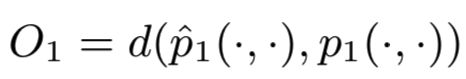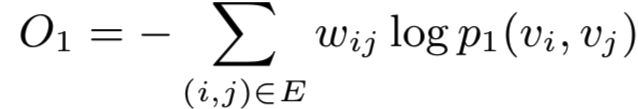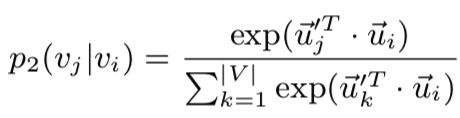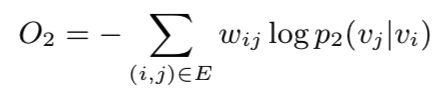【Graph Embedding】: LINE算法
论文“LINE: Large-scale Information Network Embedding”发表在WWW‘15上，提出了一个适用于大规模网络embedding算法“LINE”。
论文下载地址：https://arxiv.org/pdf/1503.03578.pdf
作者公布的代码：https://github.com/tangjianpku/LINE
介绍
本篇文章提出的算法定义了两种相似度：一阶相似度和二阶相似度，一阶相似度为直接相连的节点之间的相似，二阶相似度为存不直接相连单存在相同邻近节点的相似。还提出来一个针对带权图的边采样算法，来优化权重大小差异大，造成梯度优化的时候梯度爆炸的问题。
该方法相比于deepwalk来说，deepwalk本身是针对无权重的图，而且根据其优化目标可以大致认为是针对二阶相似度的优化，但是其使用random walk可以认为是一种DFS的搜索遍历，而针对二阶相似度来说，BFS的搜索遍历更符合逻辑。而LINE同时考虑来一阶和二阶相似度，一阶相似度可以认为是局部相似度，直接关联。二阶相似度可以作为一阶相似度的补充，来弥补一阶相似度的稀疏性。
定义
信息网络（Information Network）信息网络被定义为G(V,E),其中V是节点集合，E表示边的集合。其中每条边定义一个有序对：e=(u,v)，并分配一个权重值
用于表示点u和点v之间联系的强弱。如果为无向图的话，
,
。
一阶相似性（First-order Proximity）一阶相似性定义为两个节点之间的局部成对相似性。对于由边(u,v)链接的节点对，其链接权重用于表示节点u和节点v之间的一阶相似性，如果两个节点之间没有边相连，那么他们的一阶相似性为0。
一阶相似性固然可以直接表示节点之间的相似性，但是在真实环境下的信息网络往往存在大量的信息缺失，而许一阶相似度为0的节点，他们本质上相似度也很高。自然能想到的是那些拥有相似邻近节点的节点可能会存在一定的相似性。比如在真实环境中，拥有相同朋友的两个人也很可能认识，经常在同一个词的集合中出现的两个词也很有可能很相似。
二阶相似性(Second-order Proximity) 两个节点的二阶相似性是他们的邻近网络结构的相似性。如
表示u对全部节点的一阶相似性。那么节点u和节点v的二阶相似性由
和
决定。如果没有节点同时链接u和v，那么u和v的二阶相似度为0。
LINE with First-order Proximity
定义两个点之间的联合概率：
其中
和
是节点i和j的低纬embedding向量，直接利用sigmoid来度量两个节点的相似度。而对应的需要拟合的经验概率为
,即为全部权重的归一化后的占比，这里的
,所以对应的优化目标为：
最小化该优化目标，让预定义的两个点之间的联合概率尽量靠近经验概率。
用于度量两个分布之间的距离，作者选用来KL散度来作为距离度量。那么使用KL散度并忽略常数项后，可以得到：
这就是最终的优化目标，这里需要注意，一阶相似度只能用于无向图。
LINE with Second-order Proximity
二阶相似度同时适用于有向图和无向图。
二阶的含义可以理解为每个节点除了其本身外还代表了其所对应的上下文，如果节点的上下文分布接近那么可以认为这两个节点相似。
以有向边为例，有向边(i,j),定义节点
的上下文（邻接）节点
的概率为：
其中|V|是上下文节点的数量。其实和一阶的思路类似，这里用softmax对邻接节点做了一下归一化。优化目标也是去最小化分布之间的距离：
其中用于度量两个分布之间的差距。因为考虑到图中的节点重要性可能不一样，所以设置了参数
来对节点进行加权。可以通过节点的出入度或者用pagerank等算法来估计出来。而这里的经验分布则被定义为：
其中，
是边(i,j)的权重，
是节点i的出度，即
而N(i)就是节点i的出度节点的集合。同样采样KL散度作为距离度量，可以得到如下优化目标：
Combining first-order and second-order proximities
文章提到暂时还不能将一阶和二阶相似度进行联合训练，只能将他们单独训练出embedding，然后在做concatenate。
负采样
这个算是一个常见的技巧来，在做softmax的时候，分母的计算要遍历所有节点，这部分其实很费时，所以在分母较大的时候，经常会使用负采样技术。
边采样
也是训练的一个优化，因为优化函数中由一个w权重，在实际的数据集中，因为链接的大小差异会很大，这样的话会在梯度下降训练的过程中很难去选择好一个学习率。直观的想法是把权重都变成1，然后把w权重的样本复制w份，但是这样会占用更大的内存。第二个方法是按w权重占比做采样，可以减少内存开销。
完。