时间序列分析 - ARMA/ARIMA参数估计及模型预测
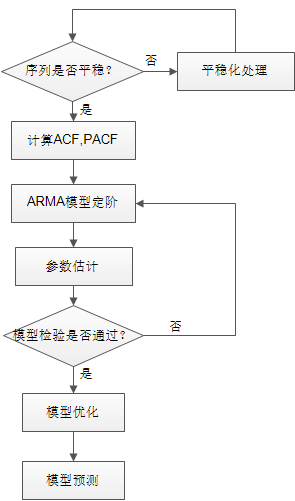
整体处理流程如下:
【平稳化处理】
根据ADF单位根检验看序列是否平稳,对于非平稳序列可以进行差分,对数等等。
对于得到的平稳序列需要检测是否为白噪声,如果是就没有必要再分析了。
【白噪声检验】
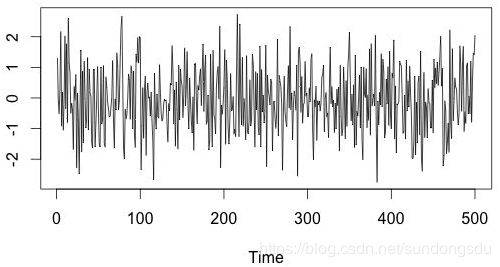
1)由于白噪声序列期望为0,方差固定。因此会在y=0上下小幅波动,比如:
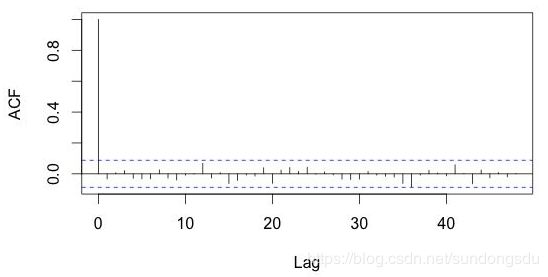
2) 白噪声仅与自己相关,任何lag时差的序列之间自相关值应该近似为0或者落在95%的置信区间以内,比如:
3) Ljung-Box Q统计量检验
p值小于5%,序列为非白噪声。
【自相关函数ACF与偏相关函数PACF】
假设时间序列在t时刻为Xt,在s时刻为Xs, 并且t-s=k
自相关函数ACF即为自相关系数:
其中![]() 为自协方差。
为自协方差。
对于平稳时间序列,方差恒定,上述公式可以写成:
![]()
偏自相关函数则是考虑了时刻t与t-k之间的所有中间时刻时间序列的影响,用公式表示为:
分母为时刻t与s的条件自协方差,分子根号内为时刻t与s各自的条件方差。
【ARMA模型p,q定阶:截尾与拖尾】
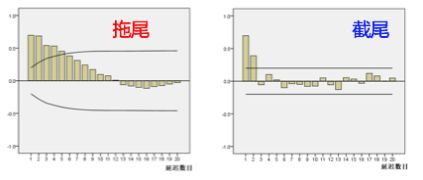
截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);不同于拖尾,拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF)。
比如:
如何判断拖尾和截尾:
(1)如果样本自相关系数(或偏自相关系数)在最初的q阶明显大于2倍标准差范围,而后几乎95%的样本自相关(偏自相关)系数都落在2倍标准差范围以内,而且由非零自相关(偏自相关)系数衰减为小值波动的过程非常突然,这时,通常视为自相关(偏自相关)系数截尾。
(2)如果有超过5%的样本相关系数落在2倍标准差范围以外,或者是由显著非零的相关函数衰减为小值波动的过程比较缓慢或者非常连续,这时,通常视为相关系数不截尾。
根据序列的自相关函数和偏自相关函数的特征可以初步判断模型类型,如下表:
| 自相关函数(ACF) | 偏自相关函数(PACF) | 选择模型 |
|---|---|---|
| 拖尾 | p阶截尾 | AR(p) |
| q阶截尾 | 拖尾 | MA(q) |
| p阶拖尾 | q阶拖尾 | ARMA(p,q) |
【模型参数估计】
可以使用最小二乘或者极大似然估计法进行参数拟合。
【模型检验】
残差分析
残差是指实际观察值与估计值(拟合值)之间的差。如果模型足够准确,残差应该为白噪声,关于白噪声的检验方式可以看文初的论述。
【模型优化】
经过模型检验可能会得到若干个模型,为了避免过拟合,从中选择最好的一个,选择的准则可以是AIC或者BIC。
AIC (Akaike information criterion,赤池信息量) 可以表示为:
AIC=2k-2ln(L)
其中:k是参数的数量,L是似然函数。假设条件是模型的误差服从独立正态分布。
让n为观察数,SSR(SUM SQAURE OF RESIDUE)为残差平方和,那么AIC变为: AIC=2k+nln(SSR/n)
优先考虑的模型应是AIC值最小的那一个,即拟合数据的同时减少参数,以避免过拟合。
BIC (Bayesian information criterion, 贝叶斯信息准则),可以表示为:
其中:
- 是模型M的极大释然估计, 极大释然估计对应的参数;
- 是观测样本;
- 是观测样本数;
- k 是模型的参数个数。
【模型预测】
根据最终模型来预测未来的数据。
参考:
https://blog.csdn.net/dingming001/article/details/73554949/
https://newonlinecourses.science.psu.edu/stat510/node/62/
https://en.wikipedia.org/wiki/Box%E2%80%93Jenkins_method
https://www.jianshu.com/p/124010e961e4
http://www.atyun.com/4462.html