Strah（所有矩形面积和 单调栈）

原题： http://acm.zjnu.edu.cn/CLanguage/showproblem?problem_id=2274

题意：

给出一个矩阵，有些地方为’#’，求所有不包含’#'的子矩阵的面积。

解析：

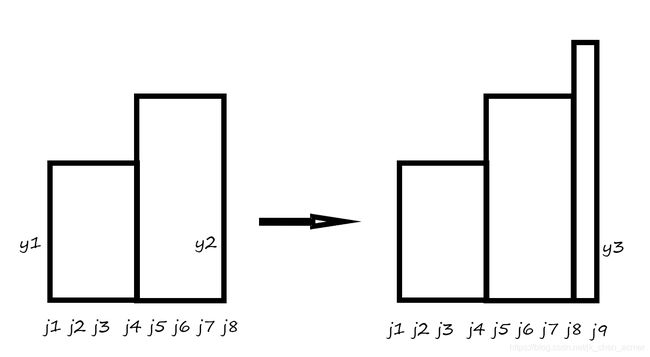
从左往右维护单调栈。用$sum\_sta$表示当前结点为右下角的所有矩形的面积和，$sum\_fy$表示上述图形的面积。

观察$(j1\_j8,y1)$这个矩形，在操作后变成了$(j1\_j9,y1)$，面积加了$y1$，$j2,j3$同。

而考虑到除了$(j1\_j8,y1)$外，还有$(j1\_j8,1),(j1\_j8,2)...(j1\_j8,y1-1)$，为了方便起见，将这些合并到$(j1\_j8,y1)$，就变成了$(j1\_j8,(1+y1)\ast y1/2)$。

那么操作后，$sum\_sta$增加的应该是$sum\_fy+(1+y3)\ast y3/2)$，$sum\_fy$增加到为$(1+y3)\ast y3/2)$。

---

接下来是$y3<y2$的情况，从栈中取出并维护即可。（上图中栈中的应该是：$j4,j8,j9$）

#include
using namespace std;
#define LL long long
int up[2009][2009];
char x[2009][2009];

LL sum_fy,sum_sta,ans;
stack<int>S;

int first;
void init(int j){
    first=j+1;
    while(!S.empty())S.pop();
    sum_fy=sum_sta=0;
}
LL Fy(int y){
    return (LL)(y*(y+1)/2);
}
void push(int i,int j){
    int h=up[i][j];
    while(!S.empty()&&up[i][S.top()]>h){
        int r=S.top();S.pop();
        int l=(S.empty()?first:S.top()+1);

        sum_fy-=(r-l+1)*Fy(up[i][r]);
        sum_sta-=(LL)((2*j-l-r)*(r-l+1)/2)*Fy(up[i][r]);
        sum_fy+=(r-l+1)*Fy(h);
        sum_sta+=(LL)((2*j-l-r)*(r-l+1)/2)*Fy(h);
    }

    if(!S.empty()&&up[i][S.top()]==h)S.top()=j;
    else S.push(j);

    sum_fy+=(LL)Fy(h);
    sum_sta+=sum_fy;
    ans+=sum_sta;
}

int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%s",x[i]+1);
    }
    for(int i=1;i<=n;i++){
        init(0);
        for(int j=1;j<=m;j++){
            if(x[i][j]=='.')up[i][j]=up[i-1][j]+1;
            else up[i][j]=0;
            if(x[i][j]=='.'){
                push(i,j);
            }
            else{
                init(j);
            }
        }
    }
    printf("%lld\n",ans);
}