「归并排序:题目一」如何实现一个空间复杂度为 O(1) 的归并排序?
今天分享一道很经典的题目,如何将归并排序是空间复杂度降低到 ,希望你看完有所收获~~
题目解析
对于一个整数数组,如何实现一个空间复杂度为 ,时间复杂度为 的归并排序?
归并排序原始的实现方式中空间复杂度为 ,现在要将其降到 ,你知道该怎么处理吗?
思考片刻...,未果。
面试官提示,那如何用 一个数保存两个数 呢?
对于数组中两个元素 arr[i] 和 arr[j],要将这两个元素保存到数组下标为 i 的数当中,我们可以通过取模和求余运算来实现。
首先找到一个比 arr[i] 和 arr[j] 都大的数 maxval ,这里我们取 max(arr[i], arr[j]) + 1 ;
然后就可以用一个数 arr[i] = arr[i] + arr[j] * maxval 来同时表示原始数组中的 arr[i] 和 arr[j] ;
原始的 arr[i] = arr[i] % maxval ,而 arr[j] = arr[i] / maxval .
举个简单的例子,比如数组中的两个元素分别为 arr[0] = 4 和 arr[4] = 3 ,maxval = max(arr[i], arr[j]) + 1 = 4 + 1 ,新的 arr[0] = arr[0] +arr[4] * maxval = 4 + 3 *5 = 19 。
原始数组中的 arr[0] = arr[0] % 5 = 19 % 5 = 4 ,而原始的 arr[4] = arr[0] / 5 = 19 / 5 = 3· 。
那么如何将这一个技巧应用到归并排序,并将其空间复杂度降至 呢?
要将空间复杂度降至 ,我们仅需要关注 merge 函数的实现,同样我们以一个例子作为说明。
最后一次合并前的数组如下所示:

此时原始数组已被分成了两个有序的子数组 [1,4,5] 和 [2,4,8] ,此时的合并步骤不再开辟两块空间的方式进行合并,而是采用我们上面讲到的技巧。
要保证数组中的任意两个数都可以用第三个数表示,我们需要将 maxval 设置为数组中的最大值加 1,即,maxval = 9 。
设置两个分别指向有序数组第一个元素的指针 i 和 j :
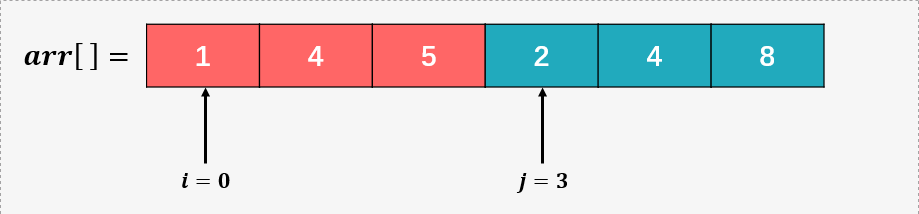
第一步,比较 arr[i] % 9 = 1 和 arr[j] % 9 = 2 , ,所以 arr[0] 的位置要保存 1,我们这里将 arr[i] 作为商,即 arr[0] = arr[0] + arr[i] * maxval = 1 + 1 * 9 = 10 ,并将指针 i 右移(合并好的元素用橘黄色表示):
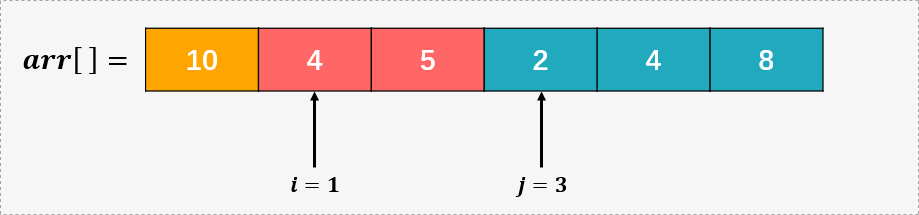
第二步,比较 arr[i] % 9 = 4 和 arr[j] % 9 = 2 , ,所以 arr[1] 的位置要保存 2,我们这里将 arr[j] 作为商数,即 arr[1] = arr[1] +arr[j] * maxval = 4 + 2 * 9 = 22 ,并将指针 j 右移:

第三步,比较 arr[i] % 9 = 22 % 9 = 4 和 arr[j] % 9 = 4 , ,所以 arr[2] 的位置要保存 arr[i] 的值,故将 arr[i] 作为商数,arr[2] = arr[2] + arr[i] * maxval = 5 + 4 * 9 = 41 ,然后将指针 i 右移。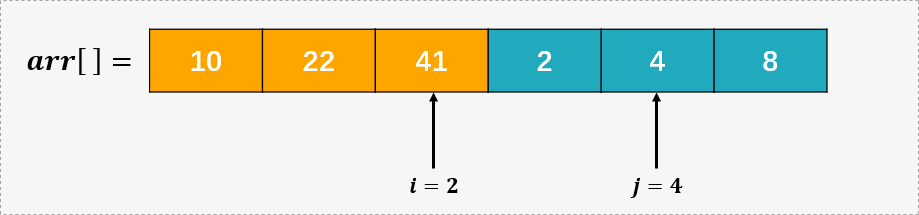
第四步,比较 arr[i] % 9 = 41 % 9 = 5 和 arr[j] % 9 = 4 , ,所以 arr[3] 的位置要保存 arr[j] 的值,故将 arr[j] 作为商数,arr[3] = arr[3] + arr[i] * maxval = 2 + 4 * 9 = 38 ,然后将指针 j 右移。
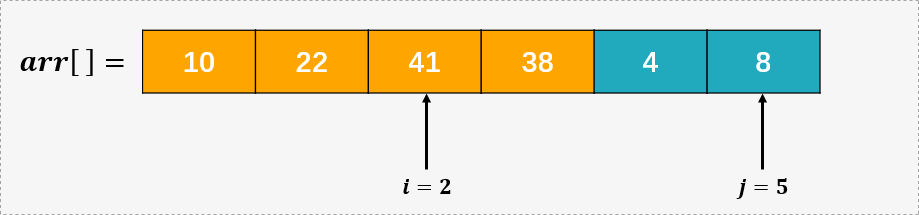
第五步,比较 arr[i] % 9 = 41 % 9 = 5 和 arr[j] % 9 = 8 , ,所以 arr[4] 的位置要保存 arr[i] 的值,故将 arr[i] 作为商数,arr[4] = arr[4] + arr[i] * maxval = 4 + 5 * 9 = 49 ,然后将指针 i 右移。

第六步,发现指针 i 已经超出了边界,j 还有越界,所以要对 j 之后剩余的元素进行处理,这里只有一个元素 arr[5] 没有处理,所以 arr[5] = arr[5] + arr[5] *maxval = 8 + 8 * 9 = 80 .
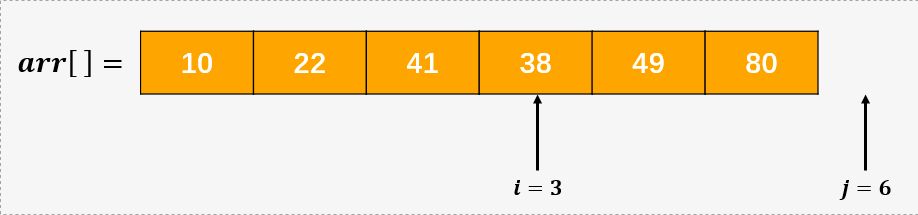
但是这并不是我们的原始数组呀,别急,接下来才是见证奇迹的时刻,我们对数组中的每一个元素除以 maxval = 9 ,会发生什么呢?我们得到了一个原始数组的有序序列,这也就是为什么每次把要保存的值作为商的原因:
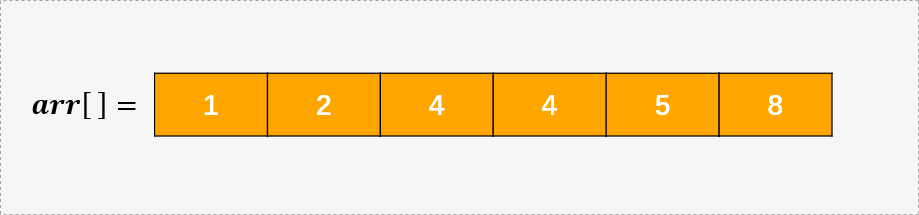
有没有很神奇?
实现代码
class MergeSortWithO1
{
static void merge(int[] arr, int left,
int mid, int right,
int maxval)
{
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= right)
{
if (arr[i] % maxval <= arr[j] % maxval)
{
arr[k] = arr[k] + (arr[i] % maxval) * maxval;
k++;
i++;
}
else
{
arr[k] = arr[k] + (arr[j] % maxval) * maxval;
k++;
j++;
}
}
while (i <= mid)
{
arr[k] = arr[k] + (arr[i] % maxval) * maxval;
k++;
i++;
}
while (j <= right)
{
arr[k] = arr[k] + (arr[j] % maxval) * maxval;
k++;
j++;
}
// 获取原始的有序序列
for (i = left; i <= right; i++)
{
arr[i] = arr[i] / maxval;
}
}
// 递归归并排序
static void mergeSortRec(int[] arr, int left,
int right, int maxval)
{
if (left < right)
{
int mid = (left + right) / 2;
mergeSortRec(arr, left, mid, maxval);
mergeSortRec(arr, mid + 1, right, maxval);
merge(arr, left, mid, right, maxval);
}
}
//找到数组的最大值,并计算出maxval,然后调用递归的归并排序
static void mergeSort(int[] arr, int n)
{
int maxval = Arrays.stream(arr).max().getAsInt() + 1;
mergeSortRec(arr, 0, n - 1, maxval);
}
}
大家有更好的解决方案也欢迎评论区留言,或者添加景禹的微信私聊奥!
推荐阅读:
原来「插入排序」面试官爱考是因为这样~~
特么,冒泡排序有这么难?
作者:景禹,一个追求极致的共享主义者,想带你一起拥有更美好的生活,化作你的一把伞。
![]()